SPSS ile Mixed Design ANOVA (Resimli)

Mixed Design ANOVA (Karışık Desen ANOVA), istatistiksel bir analiz yöntemidir ve çeşitli araştırmalarda kullanılan verilerin analizinde oldukça önemlidir. Bu yöntem, farklı faktörlerin etkisini incelemek ve bu faktörlerin etkileşimini değerlendirmek için kullanılır. Bu blog yazısında Karışık Desen ANOVA’nın ne olduğunu, varsayımlarını ve SPSS ile nasıl yapılacağını adım adım anlatacağım. Bu yöntemi kullanarak araştırmalarınızı daha fazla derinleştirebilir ve sonuçlarınızı daha güvenilir hale getirebilirsiniz.

Doğrudan ANOVA Yapma Adımlarına Geçmek İçin TIKLAYIN

Mixed Design ANOVA Nedir?

Mixed Design ANOVA (Mixed-Design Analysis of Variance), psikoloji alanında yaygın olarak kullanılan istatistiksel bir analiz yöntemidir. Bu yöntem, araştırmacılara farklı grupların veya koşulların etkilerini inceleme ve bu etkilerin zaman içinde nasıl değiştiğini anlama konusunda oldukça güçlü bir araç sunar.

“Mixed Design” terimi, bu analizin hem grup içi (within-subjects) hem de gruplar arası (between-subjects) faktörleri içeren bir tasarımı ifade eder. Yani, araştırma tasarımında hem katılımcılar üzerinde farklı zamanlarda yapılan ölçümleri (örneğin, zaman içindeki değişiklikleri inceleyen iç faktörler) hem de farklı gruplar arasındaki aynı andaki farklılıkları (örneğin, tedavi grupları arasındaki farkları inceleyen dış faktörler) ele alır.

Mixed Design ANOVA, en az iki veya daha fazla bağımlı değişkenin olduğu durumlarda kullanılır. Bu analiz, grup içi faktörlerin ve gruplar arası faktörlerin her ikisini de dikkate alarak, istatistiksel olarak anlamlı farklılıkları belirlemeye yardımcı olur. Bu sayede, araştırmacılar hem gruplar arasındaki farkları hem de zaman içindeki değişiklikleri aynı analiz içinde değerlendirebilirler.

Mixed Design ANOVA’nın avantajlarından biri, bu yöntemin hem iç faktörlerin hem de dış faktörlerin etkilerini aynı anda değerlendirebilmesidir. Bu da araştırmacılara daha kapsamlı ve derinlemesine bir perspektif sunar, çünkü aynı anda sadece bir tür değişkeni değil, her iki tür değişkeni ve bu değişkenlerin birbiriyle etkileşimini bir arada ele alabilirler.

Karışık Desen ANOVA, İngilizce kaynaklarda Mixed Design ANOVA ya da Split-Plot ANOVA olarak geçer.

Mixed Design ANOVA Varsayımları Nelerdir?

Mixed Design ANOVA’nın geçerli ve güvenilir sonuçlar elde edebilmesi için bazı varsayımlar göz önünde bulundurulmalıdır. Bu varsayımlar şunlardır:

1. Normal Dağılım Varsayımı: Bağımsız değişkenlerin grupları içindeki bağımlı değişkenin normal dağılım göstermesi önemlidir. Normal dağılımın bozuk olduğu durumlarda, normalleştirme yöntemleri veya alternatif istatistiksel teknikler kullanılabilir.
2. Homojenlik Varsayımı: Gruplar arasındaki varyansın benzer olması, yani homojen olması gerekir. Homojenlik varsayımının ihlali durumunda, özellikle küçük örneklemlerde, alternatif istatistiksel yöntemlere başvurulabilir.
3. Küresellik Varsayımı (Sphericity = Sferisite): Grup içi faktörlerin kovaryans matrislerinin eşit olması gerekmektedir. Eğer bu varsayım geçerli değilse, Greenhouse-Geisser düzeltmesi veya Huynh-Feldt düzeltmesi gibi sferisite düzeltmeleri kullanılabilir.

Bu varsayımların göz önünde bulundurulması, analizin güvenilirliğini artırmaya ve doğru sonuçlara ulaşmaya yardımcı olabilir. Eğer varsayımlar sağlanmıyorsa, alternatif istatistiksel yöntemlere başvurmak veya veri setini uygun şekilde dönüştürmek gerekebilir.

Bu varsayımların hepsini, mixed design ANOVA yaparken teker teker test edeceğiz.

SPSS ile Mixed Design ANOVA Nasıl Yapılır?

SPSS ile mixed design ANOVA analizi yapmak biraz karışık bir süreçtir. Anlaşılır olması için aşağıda görseller kullanarak, adım adım ne yapılması gerektiğini anlattım.

Bu örnekte, kadınlar ve erkeklerden oluşan katılımcılar arasında, üç farklı zamanda yapılan ölçümler arasında ve cinsiyetler arasında fark olup olmadığına mixed design ANOVA ile bakacağız.

Adım 1:

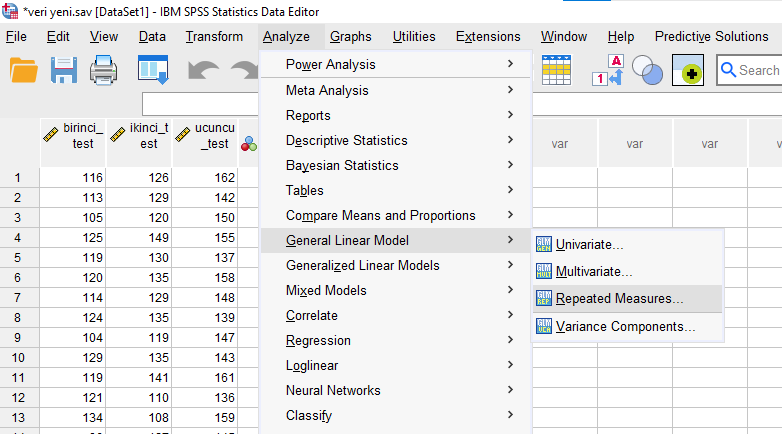
SPSS’te Analyze -> General Linear Model -> Repeated Measures butonlarına tıklayarak ANOVA analizimize başlıyoruz.

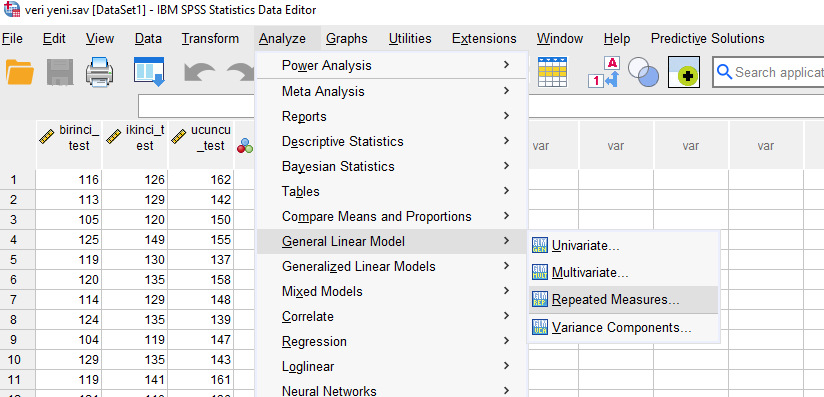
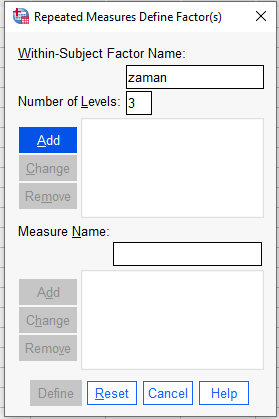
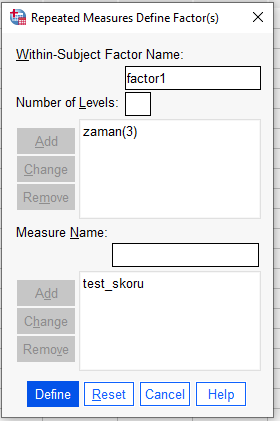
Zaman içinde tekrar tekrar ölçülmüş olan değişkenimizin ismini üstteki kutuya yazıp, kaç defa ölçüm yapıldıysa o sayıyı altındaki kutucuğa yazıyoruz. Sonra “Add” tuşuna basıp altlarındaki büyük kutuya ekliyoruz.

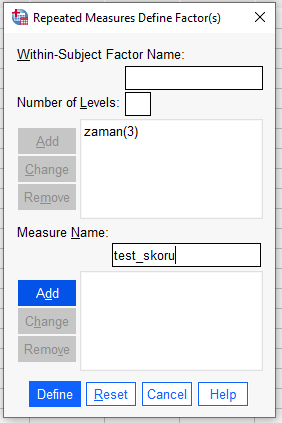
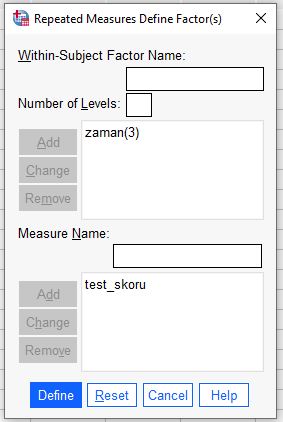
Daha sonra, farklı kişilerden oluşan grupları karşılaştırdığımız değişkenimizin ismini “Measure Name” kutucuğuna yazıp “Add”e basıyoruz.

İki kutu da dolduktan sonra “Define” tuşuna basarak ANOVA penceresini açıyoruz.

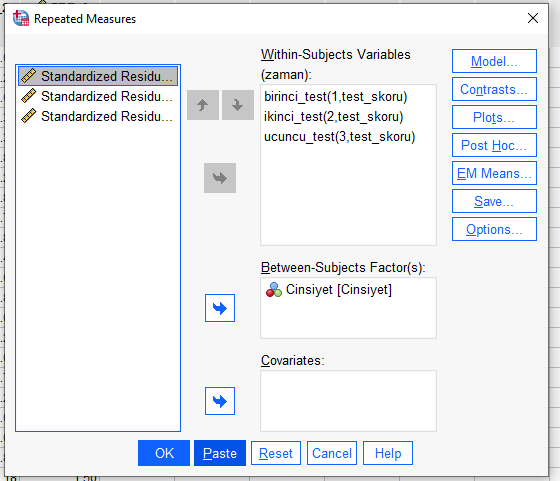
“Within-Subjects Variables” kutusunda, farklı zamanlarda kaç adet ölçüm yapıldıysa o kadar satır çıkacak. Ölçümleri, doğru sırayla soldaki kutudan sağdaki kutuya taşıyoruz. (Bu örnekte farklı zamanlardaki test skorları)

“Between-Subjects Factors” kutusuna da, karşılaştırmak istediğimiz, farklı kişilerden oluşan gruplardan oluşan değişkenimizi koymamız gerekiyor. (Bu örnekte cinsiyet)

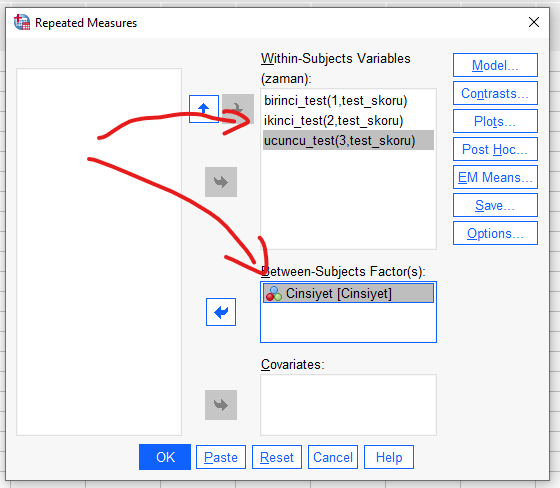
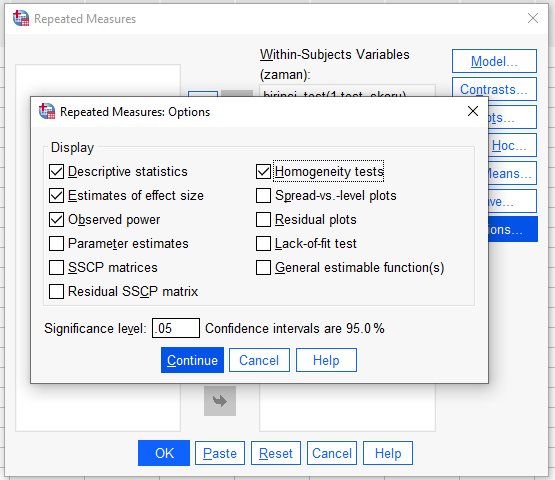
“Options” butonuna basarak, açılan pencerede aşağıdaki seçenekleri işaretliyoruz. Sonra “Continue”ya basıyoruz.

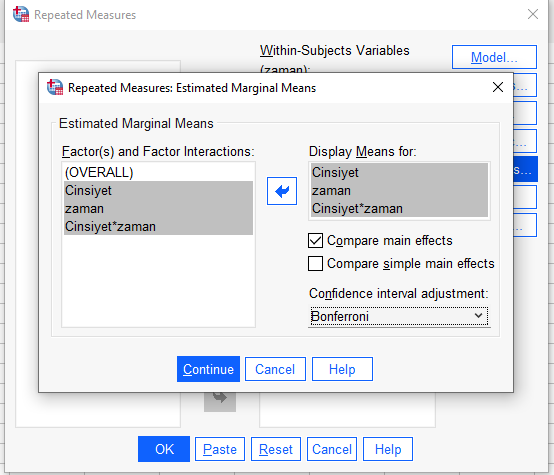
“EM Means” butonuna basarak, açılan pencerede, soldaki değişkenleri ve etkileşimlerini sağdaki “Display means for” kutusuna taşıyoruz. “Compare main effects” işaretliyoruz ve “Confidence interval adjustment”ı LSD yerine Bonferroni yapıyoruz.

LSD yerine Bonferroni yapmamız önemli çünkü LSD (Least Significant Difference = En Düşük İstatistiksel Anlamlı Fark) testinin 0.05’in altında bir p değeri gösterecek olması çok olası. Bu da, analiz sonucunun güvenilirliğini zedeler. Bunun yerine Bonferroni kullanmak, daha güvenilir p değerleri elde etmemizi sağlar.

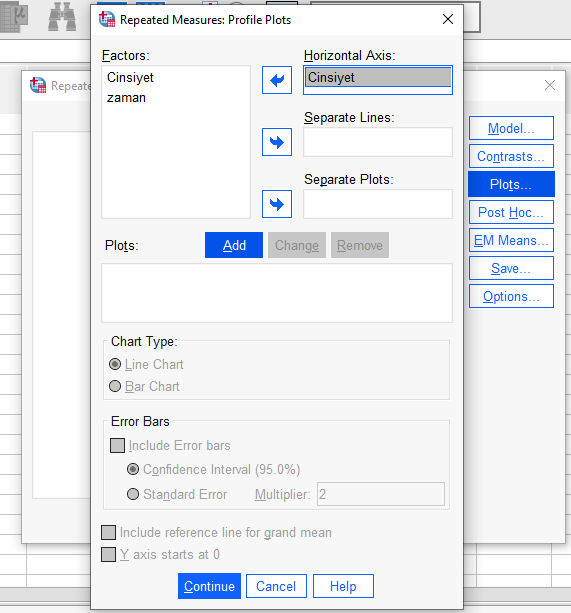
“Plots” butonuna basıp, açılan pencerede önce cinsiyeti, sonra zamanı, sonra da ikisini birden sağdaki ilgili kutulara atarak “Add”e basıyoruz. Sonrasında “Include error bars” dersek daha güzel grafikler elde etmiş oluruz. Resimleri aşağıda görebilirsiniz.

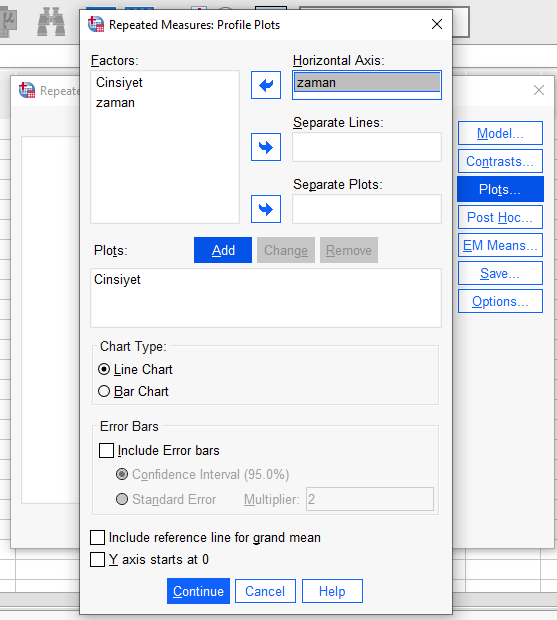
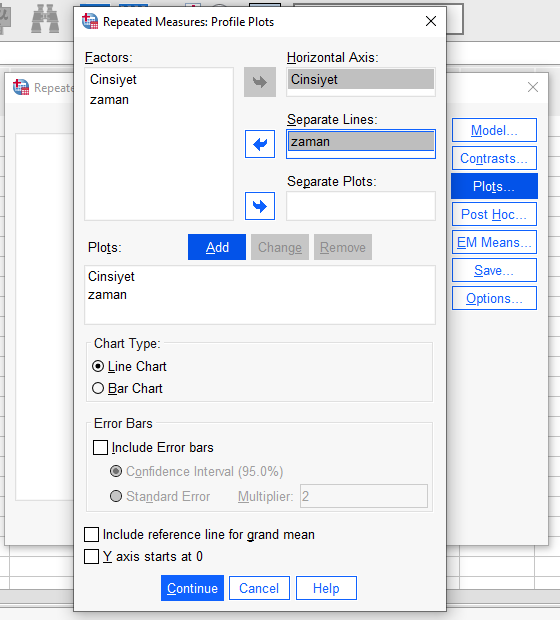
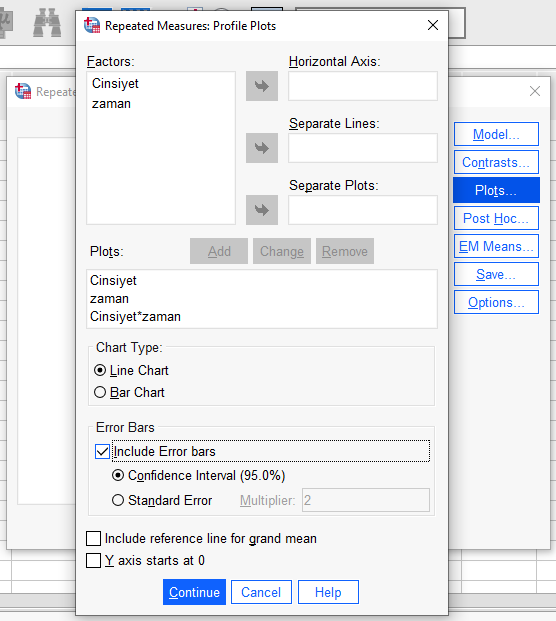
Bundan sonraki birkaç adım normallik varsayımını test etmek hakkında. Mixed design ANOVA testimizin sonuçlarını değerlendirmeden önce, normallik varsayımının doğrulandığından emin olmalıyız. Aksi takdirde, yaptığımız ANOVA’nın sonuçları yeterince güvenilir olmayabilir. Bunun için önce, ANOVA penceremizde “Save” butonuna basarak, açılan pencerede “Residuals” bölümündeki “Standardized” kutucuğunu işaretliyoruz.

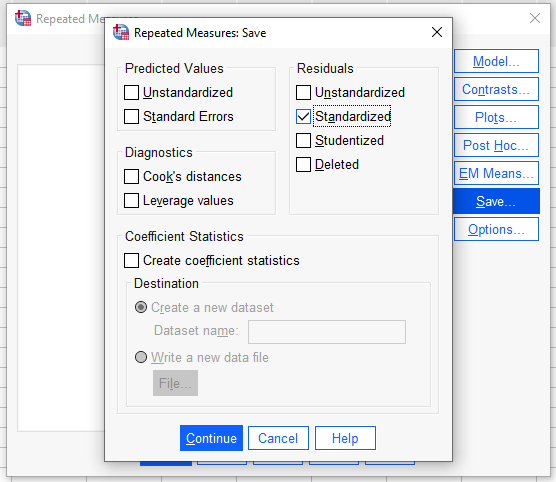
Daha sonra, SPSS sonuç ekranını aşağı alarak, SPSS verimizin bulunduğu dosyayı açarak “Data View” kısmına gidiyoruz. Orada, en sağdaki sütunun sağında 3 adet yeni sütun açılacak. Bu sütunlar “Standardized Residuals” sütunlarıdır. Bunların normal dağılıma sahip olması gerekiyor ki ANOVA sonuçlarına güvenmek için gerekli normallik varsayımı karşılanabilsin.

Residual’ların normallik varsayımını test etmek için Analyze -> Descriptive Statistics -> Explore butonlarına basıyoruz.

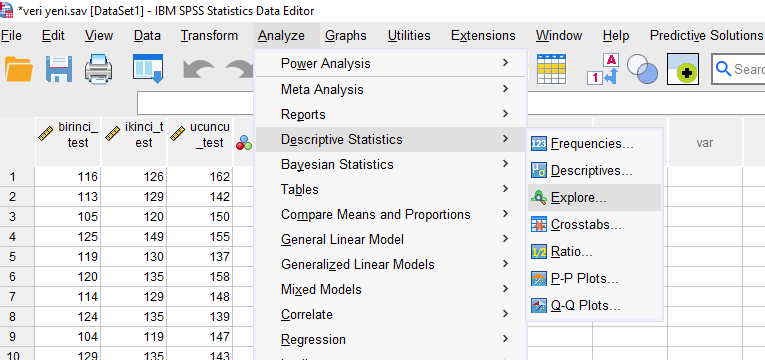
Demin oluşan Standardized Residual değişkenlerimizin hepsini Dependent List kutucuğuna atıyoruz.

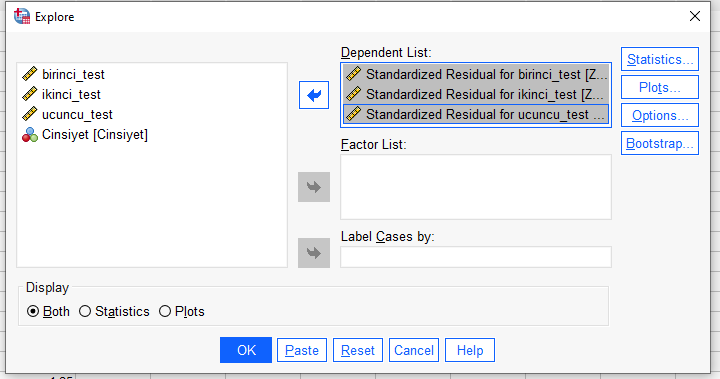
Plots’a basarak aşağıdaki resimde işaretli olan kutucukları işaretliyoruz ve Continue’ya basıyoruz. Sonra da OK’a basacağız ve karşımıza çıkan tabloları inceleyeceğiz.

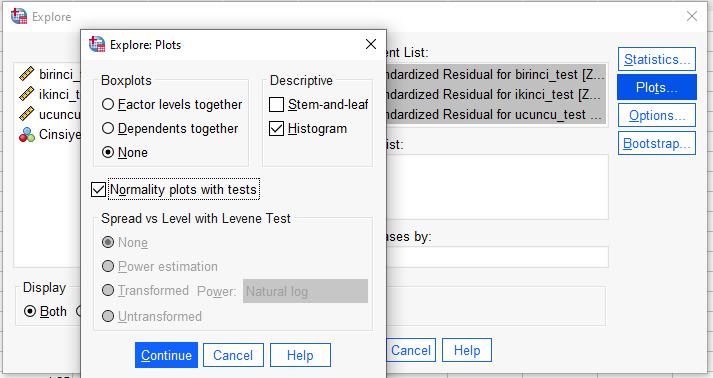
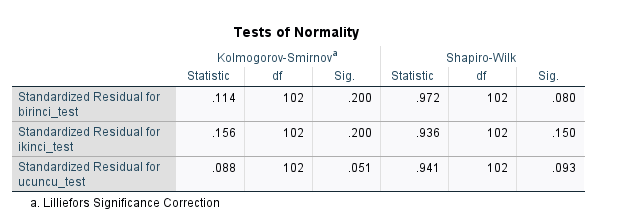
Tests of Normality tablosunda, üc değişken için de Sig. sütunundaki değere bakıyoruz. Bu değer p değeridir. Bu değerlerin hepsi 0.05’ten büyük olur ise normallik varsayımı sağlanmış diyebiliriz. Kolmogorov-Smirnov mu yoksa Shapiro-Wilk mi seçeceğiniz hakkında detaylı bir yorumlamayı normallik varsayımı yazımızda bulabilirsiniz.

Bu örnekte bütün Sig. değerleri 0.05’ten büyük çıktığı için ANOVA’mızın normallik varsayımı karşılanmış diyebiliriz.

Normallik varsayımına bakmayı bitirdikten sonra, demin SPSS’ten aldığımız ANOVA sonuçlarına geri dönelim. Küresellik (Sphericity) varsayımının sağlanıp sağlanmadığına bakmak için, Mauchly’s Test of Sphericity tablosundaki Sig. değerine bakıyoruz. Bu değer 0.05’ten büyük olur ise küresellik varsayımı doğrulanmış diyebiliriz. Bu örnekte küresellik varsayımı doğrulanmış.

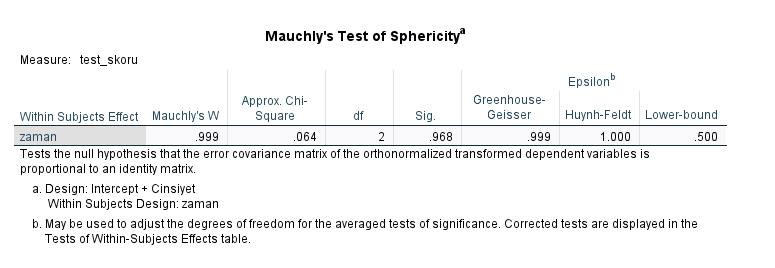
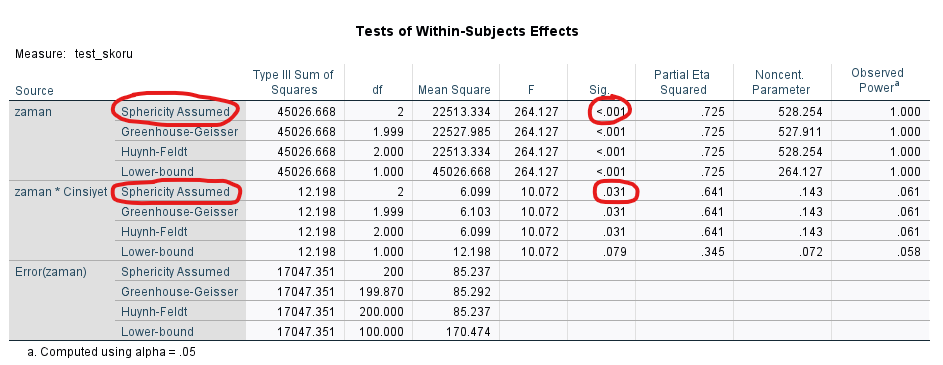
Küresellik (Sphericity) varsayımı doğrulandığı için, ANOVA sonuçlarını “Sphericity Assumed” satırından okumamız gerekiyor. Okumak gereken yerleri aşağıdaki resimde kırmızı yuvarlak içine aldım.

Zamana göre ölçümler arasında fark var mı ve zaman ve cinsiyetin etkileşimine göre ölçümler arasında fark var mı diye bakacağız aşağıdaki tabloda.

Zaman ve zaman*cinsiyet değişkenlerinin ANOVA Sig. değerleri yani p değerleri 0.001’den küçük çıkmış. Yani istatistiksel olarak anlamlı sonuçlar var demek oluyor bu.

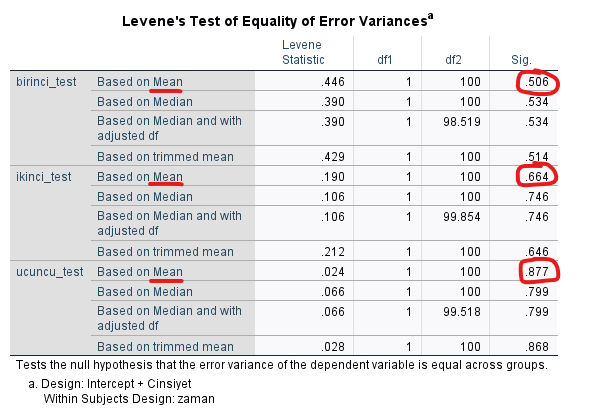
Homojenlik varsayımının doğrulanmasını da Levene’s Test ile kontrol ediyoruz. Levene’s Test of Equality of Variances tablosunda Based on Mean satırındaki Sig. değeri, Levene’s Test’imizin p değerini gösteriyor. Bu değer 0.05’ten yüksek ise homojenlik varsayımı doğrulanmış diyebiliriz. Bu örnekte p = 0.506 çıktığı için homojenlik varsayımı doğrulanmış diyoruz.

Homojenlik varsayımı doğrulandığı için, cinsiyetler arası fark var mı yok mu diye bakmak için Tests of Between-Subjects Effects tablosunda Cinsiyet satırındaki Sig. değerine bakıyoruz. Sig. yani p değeri 0.426 çıkmış. Bu değer 0.05’ten büyük olduğu için, cinsiyetler arası istatistiksel olarak anlamlı bir fark yok sonucuna varabiliriz.

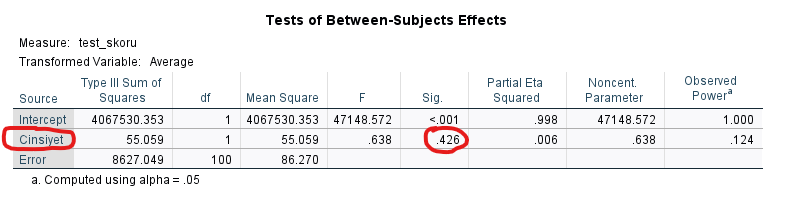
Sonuç olarak, “zaman” ve “zaman x cinsiyet” etkileşimi değişkenlerine baktığımızda, farklı ölçümler arasında istatistiksel olarak anlamlı bir fark bulunduğunu gördük.

Şimdi, hangi ölçümler arasında fark olduğunu görmek için, ek bir analiz yapacağız.

Analyze -> General Linear Model -> Repeated Measures butonlarına basıp mixed design ANOVA penceremizi tekrar açalım.

Faktörlerin yine yerlerine doğru şekilde yerleştiğinden emin olalım.

ANOVA penceresinde, “Paste” butonuna basalım ve SPSS’in kodlama yapılan bölümüne geçiş yapalım.

Merak etmeyin, burası kodlama yapmayı bilmenizi gerektirmez, sadece birkaç kod satırı kopyala – yapıştır yapacağız.

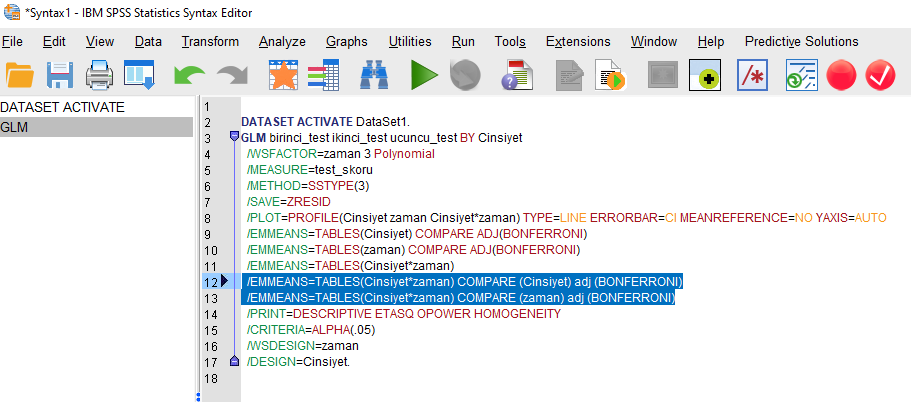
Aşağıdaki satırları, SPSS ekranında görünen yere ekliyorum. Buradaki değişkenler benim yaptığım analizin değişkenleri. Siz bu değişkenleri kendi analizinizde karşılık gelen değişkenlerin isimleriyle değiştirirsiniz.

/EMMEANS=TABLES(Cinsiyet*zaman) COMPARE (Cinsiyet) adj (BONFERRONI)
/EMMEANS=TABLES(Cinsiyet*zaman) COMPARE (zaman) adj (BONFERRONI)

Bunları ekledikten sonra, üstteki yeşil üçgen “Oynat” tuşuna basıyoruz (ekranda en üstte Utilities’in altında).

SPSS bize spesifik olarak hangi gruplar ve hangi ölçümler arasında fark olduğunu gösteren Pairwise Comparisons tablolarını sunuyor.

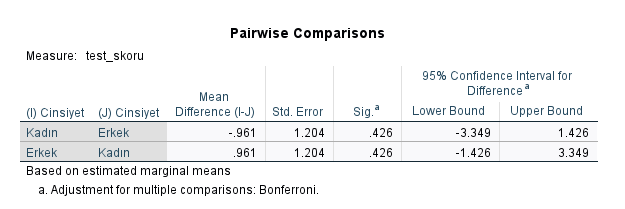
İlk Pairwise Comparisons tablosunda, cinsiyetler arasında fark olmadığını görebiliyoruz (p = 0.426 çünkü).

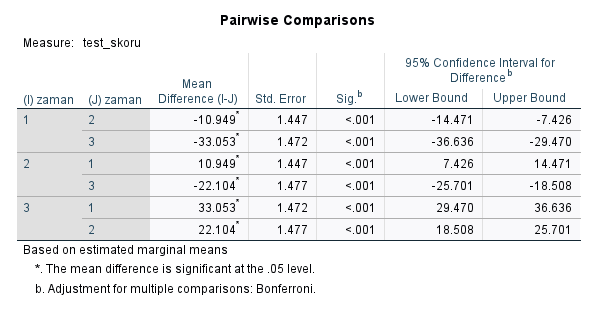
İkinci Pairwise Comparisons tablosunda, 1. ölçüm zamanı, 2. ölçüm zamanı ve 3. ölçüm zamanının her çiftinin arasında anlamlı bir fark olduğunu görebiliyoruz (bütün p değerleri 0.001’den küçük çıkmış çünkü).

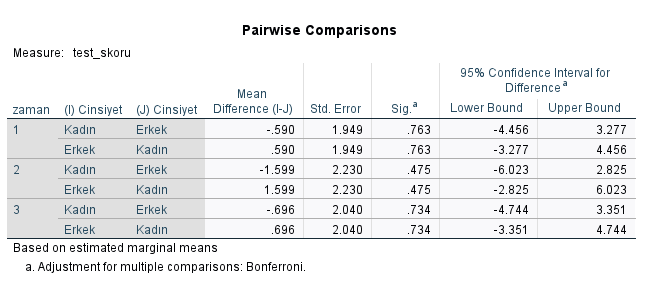
3. Pairwise Comparisons tablosunda, zamana bağlı cinsiyet değişkenlerinin arasında anlamlı fark var mı yok mu onu görebiliyoruz. Bütün Sig. değerleri 0.05’ten büyük çıkmış, yani hangi zaman diliminde ölçülmüş olursa olsun, cinsiyetler arasında istatistiksel olarak anlamlı bir fark bulunmamakta.

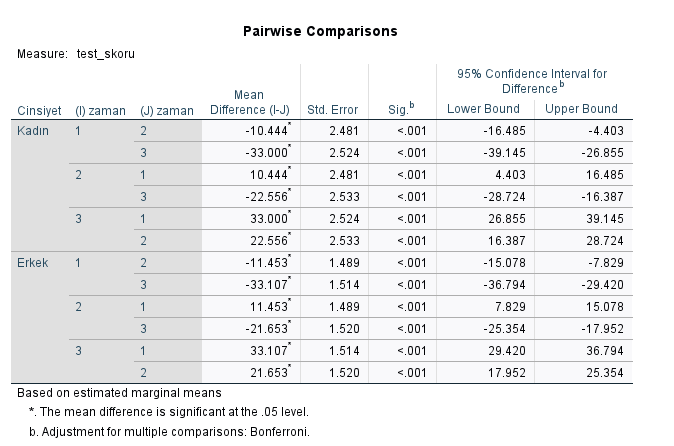
4. Pairwise Comparisons tablosunda, cinsiyete bağlı olarak ölçüm zamanları arasında anlamlı bir fark olup olmadığı gösteriliyor. Bütün Sig. değerlerinin 0.001’den küçük çıkmasından anlayacağımız üzere, iki cinsiyetin de kendi içindeki ölçümler, ölçüm zamanına göre istatistiksel olarak anlamlı bir şekilde değişiyor.

Mixed Design ANOVA Tablo Yorumlama

Özetle, Mixed Design ANOVA sonuçlarını değerlendirirken dikkate almanız gereken bazı önemli noktalar şunlardır:

1. Temel ANOVA Sonuçları:
   • Grup içi faktörlerin ve gruplar arası faktörlerin etkilerini değerlendiren ana ANOVA sonuçlarına bakın.
   • İlgili F değerleri, p değerleri ve etkileşimlerle ilgili bilgileri gözden geçirin.
2. Etkileşimlerin Anlamlılığı:
   • Mixed Design ANOVA’nın gücü, grup içi faktörlerle gruplar arası faktörler arasındaki etkileşimleri değerlendirmesidir.
   • Eğer bu etkileşim anlamlıysa, grup içi ve gruplar arası faktörlerin etkileri birlikte değerlendirilmelidir.
3. Greenhouse-Geisser veya Huynh-Feldt Düzeltmeleri:
   • Eğer küresellik (sphericity) varsayımı ihlal edilmişse, Greenhouse-Geisser veya Huynh-Feldt düzeltmelerini dikkate alın.
   • Bu düzeltmeler, grup içi faktörlerin etkilerini değerlendiren p değerlerini düzeltebilir.
4. Partial Eta-Squared (η²) Değerleri:
   • Partial (kısmi) η² değerleri, grup içi faktörlerin ve gruplar arası faktörlerin varyansın ne kadarını açıkladığını gösterir.
   • Büyük η² değerleri, faktörlerin etkilerinin büyük bir kısmını açıklar.
5. Post Hoc Test Sonuçları (Opsiyonel):
   • Eğer etkileşim anlamlıysa, post hoc test sonuçlarına bakarak spesifik gruplar arasındaki farkları belirleyin.
   • Bonferroni, Tukey, veya Scheffé gibi post hoc testlerle çoklu karşılaştırmaları düzeltmek için uygun düzeltmeleri uygulayın.
   • Bu sayfadaki örnekte, spesifik gruplar arasındaki farklılıkları “Pairwise Comparisons” tablosundan görebildiğimiz için, post hoc testi yapmamız gerekmedi.
6. Grafiklerin İncelenmesi:
   • Sonuçları görselleştirmek için uygun grafikleri inceleyin. Örneğin, etkileşim efektini gösteren bir çizgi grafiği kullanabilirsiniz.

Mixed Design ANOVA sonuçlarının bu faktörleri göz önünde bulundurarak değerlendirilmesi, elde edilen istatistiksel bilgilerin araştırmanın amacına uygun bir şekilde yorumlanmasına yardımcı olacaktır.

Mixed Design ANOVA Kısmi Eta Kare Yorumlama

Mixed Design (Karışık Desen) ANOVA sonrasında elde edilen kısmi eta kare değerleri (η²), analizin etki büyüklüğünü anlamak açısından önem taşır. Bu değerler, bağımsız değişkenlerin ve etkileşimlerin bağımlı değişken üzerindeki toplam varyans içindeki payını ölçer. İlk adım, bu değerlere genel bir bakış atmaktır. Kısmi eta kare değerleri genellikle 0 ile 1 arasında değer alır ve küçük, orta veya büyük etki büyüklükleri olarak sınıflandırılır.

ANOVA analizimizdeki değişkenlerimizin analizinin kısmi eta kare değerlerini ilgili satırın Partial Eta-Squared sütununda bulabiliriz.

Zaman değişkenimizin kısmi eta kare değeri 0.725 çıkmış.

Zaman * cinsiyet etkileşimi değişkenimizin kısmi eta kare değeri 0.641 çıkmış.

Cinsiyet değişkenimizin kısmi eta kare değeri de 0.006 çıkmış. Bu değerin üstteki tablodaki değere göre çok küçük olması normal çünkü cinsiyet değişkeninin ANOVA sonucu p değeri 0.05’ten büyük çıkmış yani cinsiyetin test skoruna anlamlı bir etkisi yok. O zaman etki büyüklüğünün de 0’a çok yakın çok küçük bir sayı çıkması normaldir.

ANOVA analizimizin tamamı bu kadardı. Cinsiyete, zamana ve zamanın cinsiyetle etkileşimine baktık ve analiz ettik, anlamlı sonuçları daha derinlemesine inceledik ve etki büyüklüğünü hesapladık. İsterseniz verileri grafiklerle görselleştirebilir ve son olarak analiz hakkında APA standartlarına uygun bir rapor yazabilirsiniz.

Araştırmayı yaparken bu yazıdan bir miktar daha teknik detaylı bir dil içeren İngilizce çok güzel bir Mixed Design ANOVA PowerPoint sunumu buldum, onun linkini de isteyenler için buraya bırakıyorum.