Kısmi Korelasyon Analizi (SPSS) — Resimli

Kısmi korelasyon analizi, bağımsız ve bağımlı değişkenler arasındaki ilişkiyi incelerken üçüncü bir değişkenin bu ilişkiye etkisini kontrol etme imkanı sunar. Bu analiz, değişkenler arasındaki ilişkinin, kontrol değişkenlerinin etkisinden arındırılarak incelenmesine olanak sağlar. Bu sayede, araştırmacılar iki değişken arasındaki ilişkiyi daha doğru bir şekilde değerlendirebilirler. Bu yazıda, kısmi korelasyon analizinin ne olduğunu ve SPSS ile nasıl yapılabileceğini göstereceğim.

Kısmi Korelasyon Nedir?

Kısmi korelasyon, belirli bir değişken çifti arasındaki ilişkinin, diğer değişkenlerin etkisinden arındırılarak ölçülmesi sonucu bulunan korelasyondur. Bu diğer değişkenlere “kontrol değişkeni” denir. Kısmi korelasyon, kontrol değişkenlerinin etkisi altında kalmadan, iki değişken arasındaki doğrudan olan ilişkiyi belirlemek için kullanılır.

Kısmi korelasyon analizi, kontrol değişkenlerinin etkisini kontrol ederek değişkenler arasındaki ilişkiyi daha net bir şekilde anlamamızı sağlayan önemli bir istatistiksel araçtır. Bu analiz, araştırmacılara iki değişkenin doğrudan etkisi dışındaki değişkenlerin girdiği modellerdeki karmaşık ilişkileri anlama ve değişkenler arasındaki bağlantıları daha doğru bir şekilde belirleme imkanı sunar.

SPSS ile Kısmi Korelasyon Analizi Nasıl Yapılır?

Bu örnekte, katılımcıların Zeka seviyesi ile Başarı seviyesi arasındaki ilişkiyi inceleyeceğiz. Bunu yaparken, katılımcıların Gelir durumunun bu ilişkiye etkisini kontrol edeceğiz, yani Gelir durumu kontrol değişkeni olacak.

Önce, değişkenlerin üçünün de birbiriyle korelasyon miktarlarına bakalım. (Tabii korelasyon analizine başlamadan önce korelasyon analizi için gerekli bütün varsayımların sağlandığından emin olduk.)

Analyze -> Correlate -> Bivariate

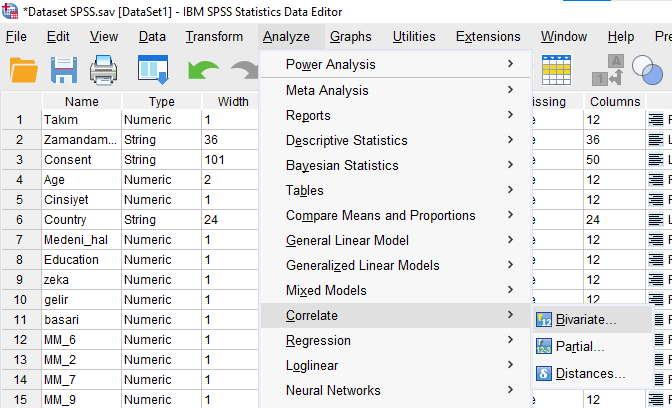
Korelasyonuna bakmak istediğimiz değişkeni ve kontrol değişkenimizi birlikte Variables kutusuna atıyoruz.

Correlations tablosunda, her değişken çiftinin birbiriyle korelasyon miktarını görebilirsiniz. Kırmızı ile altını çizdiğim yerler korelasyonun istatistiksel anlamlılık p değeri (0.05’ten küçük ise anlamlı bir ilişki var demek oluyor), mavi ile altını çizdiğim yerler de korelasyon seviyesi (0 ile 1 arasında değişebiliyor).

Buna göre üç değişkenin de birbirleriyle anlamlı bir korelasyonu varmış.

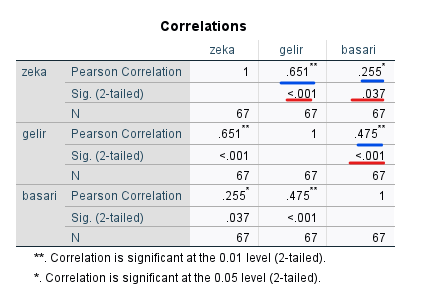
Yukarıdaki korelasyon tablosuna göre, Zeka seviyesi ile Başarı miktarı arasında 0.255’lik bir korelasyon ilişkisi varmış ve bu ilişki istatistiksel olarak anlamlıymış.

Şimdi, Gelir seviyesi değişkeninin etkisini kontrol ederek, Zeka ile Başarı arasındaki ikili korelasyon ilişkisinin gücüne bir daha bakalım.

Analyze -> Correlate -> Partial

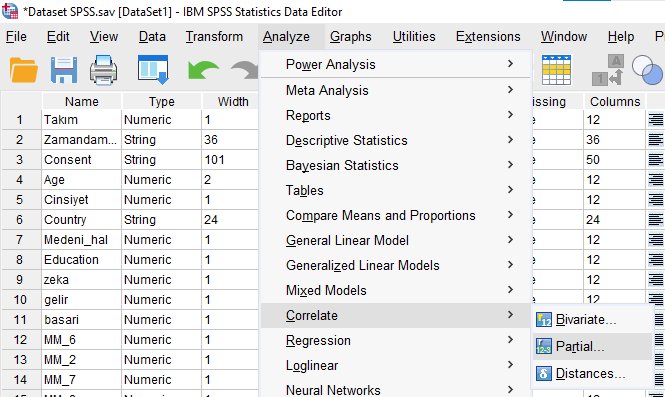
Korelasyonuna bakacağımız değişkenleri Variables, kontrol değişkenini Controlling For kutusuna atıyoruz.

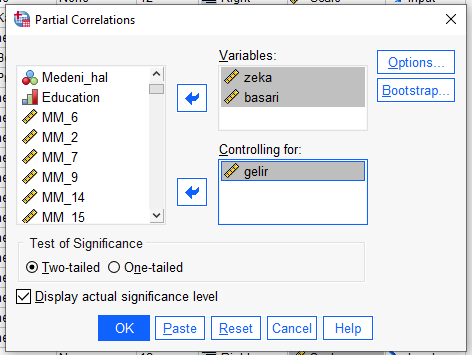
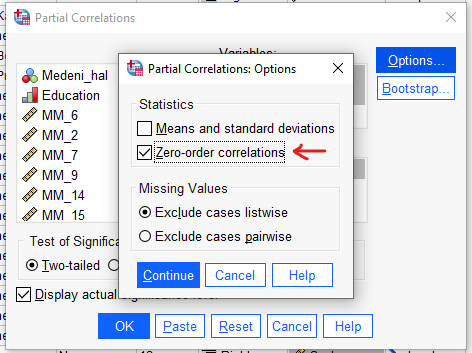
“Options”a basarak, Zero-order correlations’u işaretlersek daha detaylı bir tablo alacağız.

Kontrol değişkeni ile yeni yaptığımız korelasyon analizi sonucunda gelen Correlations tablosuna göre, Gelir seviyesi kontrol altında tutulduğunda, Zeka ile Başarı arasında istatistiksel olarak anlamlı bir ilişki bulunmamakta. Kırmızıyla işaretlediğim gibi, demin 0.037 olan p anlamlılık seviyesi şimdi 0.518 olmuş (0.05’ten büyük yani anlamsız demek). Korelasyon miktarı da 0.255’ten 0.081’e düşmüş yani 0’a yakın bir korelasyon (yani korelasyon yok demek).

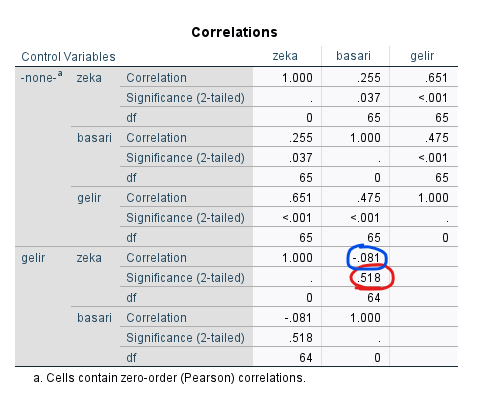
Demek ki, Gelir seviyesinin, Zeka ile Başarı arasındaki ilişkiye olan etkisi kontrol altında tutulduğunda, Zeka & Başarı arasında anlamlı bir ilişki bulunmuyormuş. Yani Zeka ile Başarı arasında ilk başta bulduğumuz ilişki, aslında Zeka’nın da Başarı’nın da Gelir seviyesi ile korelasyon ilişkisi içinde olması sonucu meydana gelmiştir ve bu ilişkileri yansıtmaktadır, Zeka ile Başarı arasında, Gelir seviyesi’nden izole olmuş herhangi bir ilişki yoktur.

Kısmi Korelasyon Grafiği Oluşturma

Zeka ile Başarı’nın, Gelir seviyesinin etkisinden arındırılarak gözlemlenen korelasyonunun grafiğini çizelim.

SPSS programını kullanarak, iki değişken arasındaki, üçüncü bir kontrol değişkeninin etkisi kontrol altında tutulduğu zamanki Kısmi Korelasyon ilişkisini grafik olarak göstermenin tek tıkla yapılabilecek bir yolu yok. Ama birkaç adımdan oluşan bir yolu var. Aşağıda bunu göstereceğim, bunu gösteren İngilizce’de bile fazla kaynak yok, Türkçe’de hiç yoktur eminim.

Başlayalım.

Önce, kontrol değişkeninin, korelasyon ilişkisine baktığımız iki değişken ile teker teker ilişkisine bakmak için yapılacak farazi bir lineer regresyon analizi sonucu oluşacak artık‘larını (residual‘larını) yeni bir değişken olarak oluşturacağız.

Analyze -> Regression -> Linear

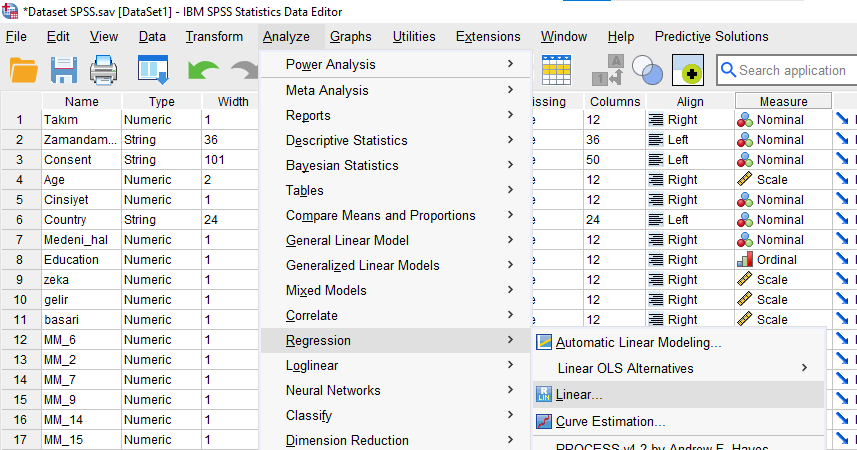
Regresyon penceresinde, demin korelasyonuna bakıyor olduğumuz değişkenlerin bir tanesini Dependent, kontrol değişkenimizi de Independents kutusuna atıyoruz.

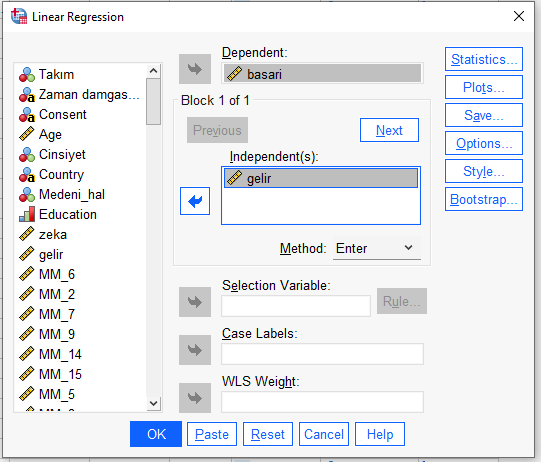
“Save”e basıp Unstandardized Residual’ı işaretliyoruz.

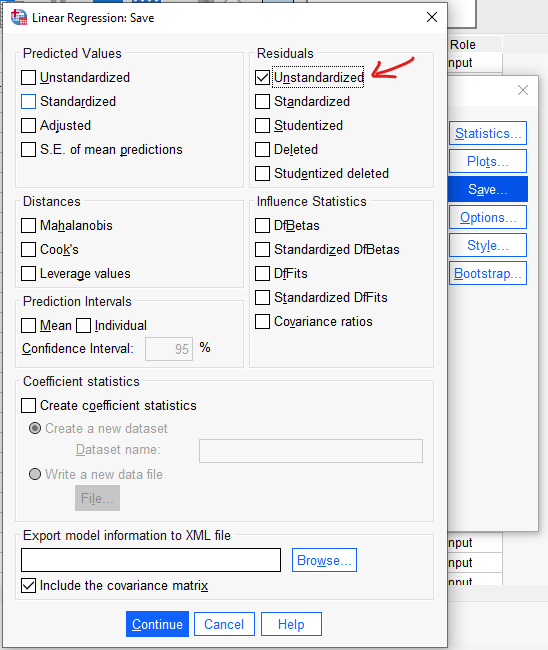
Continue ve OK’a basıp SPSS veri setimizin Data View bölümüne dönersek, en sağ sütunda yeni bir değişken için ekstra bir sütun açılmış olduğunu göreceksiniz. Bu sütunda, Gelir seviyesinin Başarı’yı belirleme miktarına bakılan regresyon analizi sonucu oluşan artık yani residual değerleri bulunur.

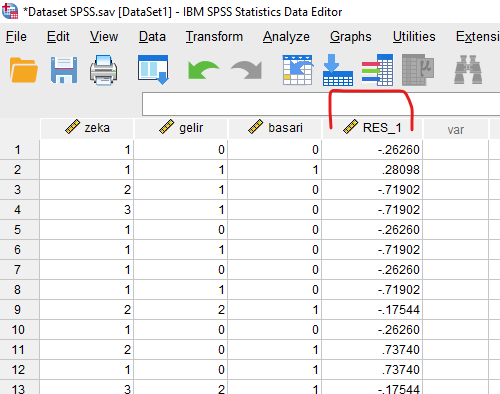
Şimdi yine Analyze -> Regression -> Linear basıp, bu sefer Gelir’in Zeka’yı belirleme miktarını gözlemlemek amacıyla oluşturulacak farazi bir regresyon analizi gerçekleştiriyoruz. Başarı’yı sola atıp Zeka’yı onun yerine koyuyoruz.

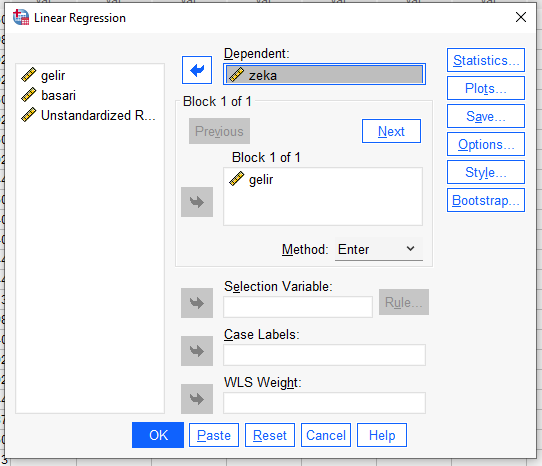
En sağda, bu sefer bu farazi regresyon analizi için oluşan artık (residual) değerleri için yeni bir sütun açılmış oldu.

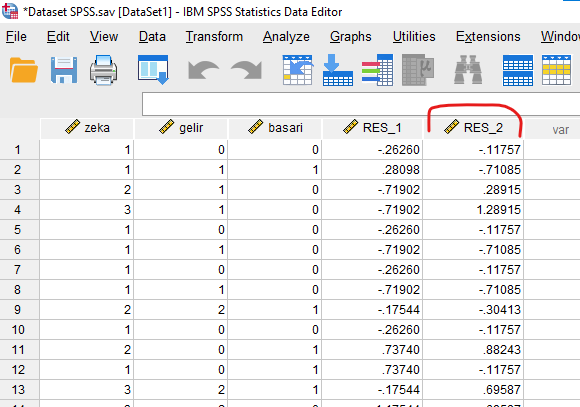
Şimdi, Analyze -> Correlate -> Bivariate butonlarına basalım ve bu iki artık residual değer‘in birbiriyle olan korelasyon ilişkisine bakalım.

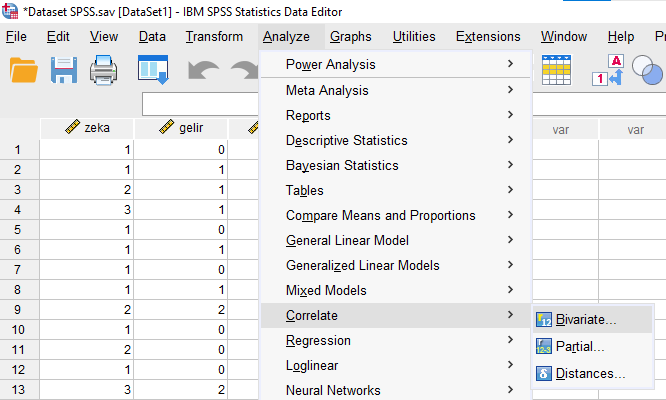
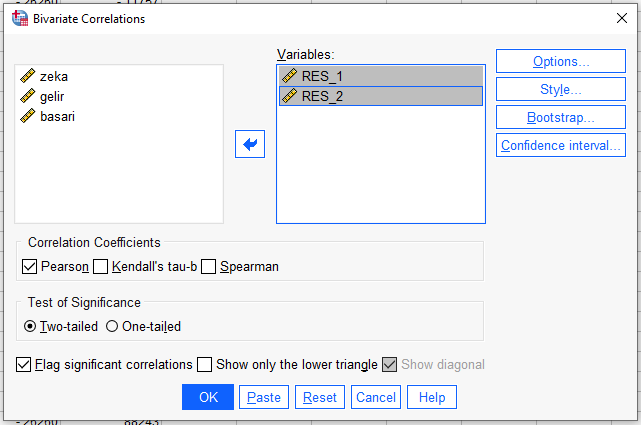
Yeni oluşmuş olan iki değişkeni Variables kutusuna atalım ve OK’a basalım.

Correlations tablosunda, iki Residual’ın birbiriyle korelasyonunu görüyoruz. Dikkat ettiyseniz, bu korelasyon demin Gelir seviyesi kontrol edildiğinde Zeka ile Başarı arasında bulduğumuz korelasyonun birebir aynısı.

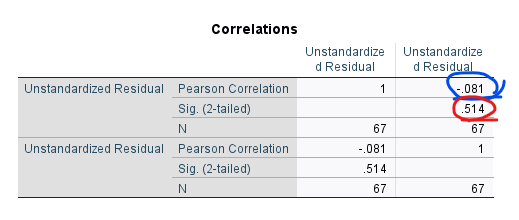
Yani kontrol değişkeninin kontrol edildiği bir korelasyon, aslında o değişkenin korelasyona giren değişkenlerle olan regresyonundan kalan residual’ların korelasyonu demektir.

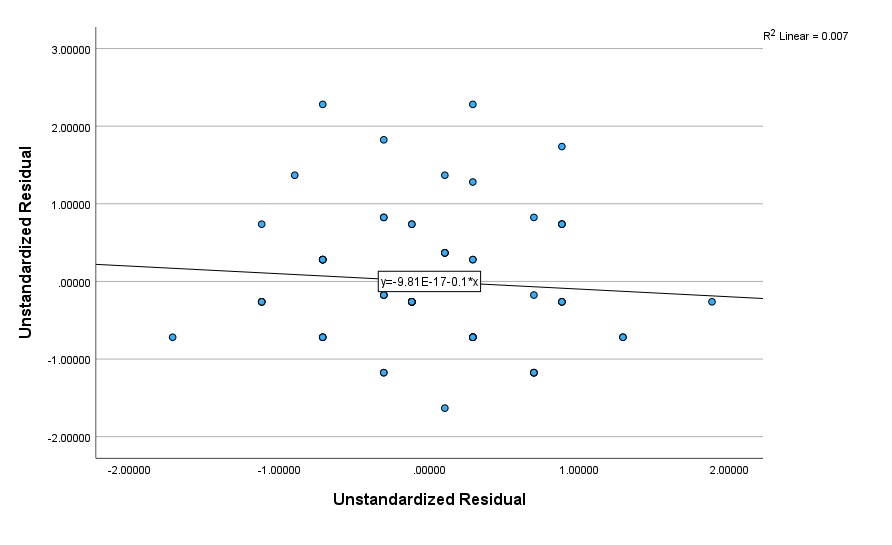
Şimdi bu korelasyonun grafiğini çizelim.

Graphs -> Scatter/Dot

Simple Scatter seçiyoruz.

X ve Y Axis kutularına Residual değişkenlerimizi koyuyoruz.

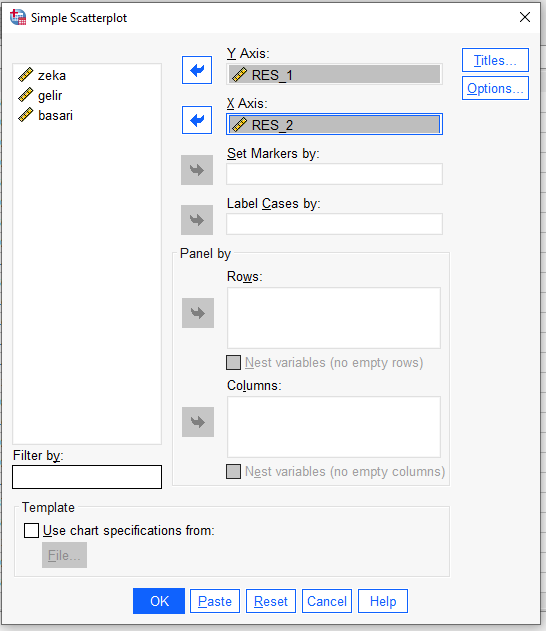
Ve karşımızda, kontrol değişkeni tarafından kontrol edildiği durumda, iki değişken arasındaki korelasyon ilişkisinin nokta grafiği.