SPSS ile Çoklu Regresyon (Forced Entry) — Resimli

Bu yazımızda, çoklu doğrusal regresyon analizi yaparken tercih edebileceğimiz “Forced Entry” metodunun ne olduğuna, SPSS ile nasıl yapılacağına, ve sonuç tablolarının nasıl yorumlanması gerektiğine bakacağız.

Çoklu Regresyon “Forced Entry” Metodu Nedir?

Forced Entry, çoklu doğrusal regresyon analizinde kullanılan bir yöntemdir. Çoklu regresyonda amaç, bir bağımlı değişken ile birden fazla bağımsız değişken arasındaki ilişkiyi modellemektir. Forced Entry metodu, regresyon modeline tüm bağımsız değişkenlerin aynı anda sokulduğu (önem sırasına bakılmaksızın) yöntemi ifade eder.

Değişkenlerin belirli kriterlere göre eklendiği veya çıkarıldığı hiyerarşik ve stepwise regresyon yöntemlerinin aksine, Forced Entry yöntemi, analizde belirtilen tüm bağımsız değişkenleri aynı anda denkleme sokmaya dayanır. Bu yaklaşım genellikle araştırmacıların, bireysel istatistiksel önemlerine bakılmaksızın seçilen tüm değişkenlerin modele dahil edilmesi gerektiğine inanmak için teorik bir nedeni olduğunda kullanılır.

Mesela, “exploratory” yani “keşfedici” deney tasarımlarında, yani hakkında ön bilgi yeterince bulunmayan bağımsız değişkenlerin hangilerinin bağımlı değişkeni etkileyip hangilerinin etkilemediğine bakmayı içeren deney tasarımlarının istatistiksel analizi yapılırken kullanılır.

Forced Entry Çoklu Regresyon Varsayımları

SPSS’te yapacağımız forced entry çoklu regresyon analizinde bulduğumuz sonuçlara güvenebilmemiz için, verimizin regresyon analizi öncesinde bazı varsayımları sağlıyor olması gerekir. Bu varsayımlar şunlardır. Varsayımları burada listeleyip, bir sonraki başlığın altında SPSS ile nasıl bakılacağını tarif edeceğim.

1. Bütün bağımsız ve bağımlı değişkenlerin devamlı veri tipinde olması gerekir.
2. Bağımlı değişkenin (ya da daha iyisi Residual’ların) normal dağılım göstermesi gerekir.
3. Veride outlier yani uç değer olmaması gerekir.
4. Her bağımsız değişken, tek başına ele alındığında, eğer bağımlı değişkenle 0.30’dan fazla korelasyon gösteriyorsa, bu korelasyonun şekli doğrusal yani lineer olmalıdır.
5. Bağımsız değişkenlerin herhangi ikisini ele aldığımızda, bu iki değişkenin birbiriyle 0.70’ten fazla korelasyon göstermemesi gerekir. (Çoklu Doğrusallık Varsayımı)

SPSS ile Forced Entry Çoklu Regresyon Varsayımları Test Etme

Normalde istatistiksel testlerde önce varsayımları kontrol edip ondan sonra testi yapmaya başlıyorduk. Forced entry çoklu regresyon varsayımlarını ise, regresyonu yaptıktan sonra tabloları okuyarak ve üzerine bir-iki ayrı küçük test yaparak kontrol ediyoruz. Bu yüzden hemen aşağıdaki başlığı tamamen takip ederseniz, hem forced entry çoklu regresyon yapma adımlarını, hem de varsayım test etme adımlarını birlikte göreceksiniz.

SPSS ile Forced Entry Çoklu Regresyon Nasıl Yapılır?

SPSS’te forced entry çoklu regresyon için aşağıdaki adımları takip edebiliriz.

Bu sayfada yapacağımız örnekte, 3 bağımsız, 1 bağımlı değişkenimiz var. Depresyon, dayanıklılık ve stres faktörlerinin, yorgunluk seviyesiyle ilişkisine bakacağız.

Analyze -> Regression -> Linear

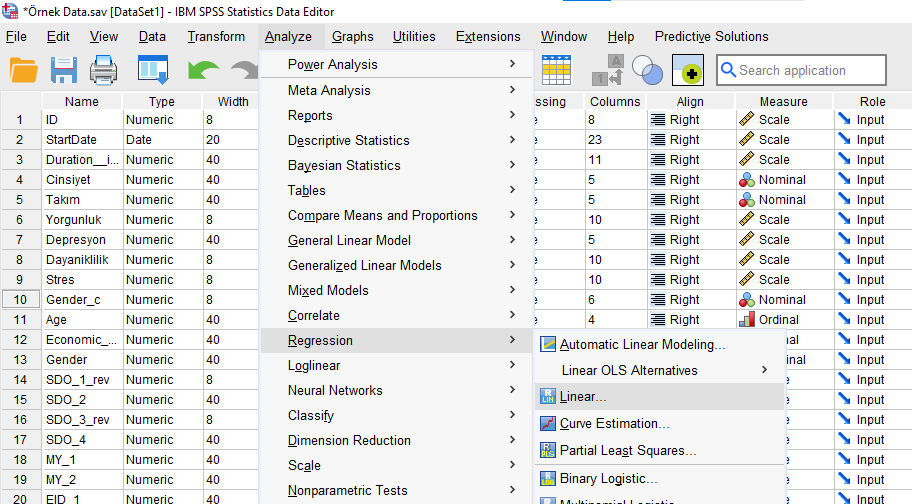
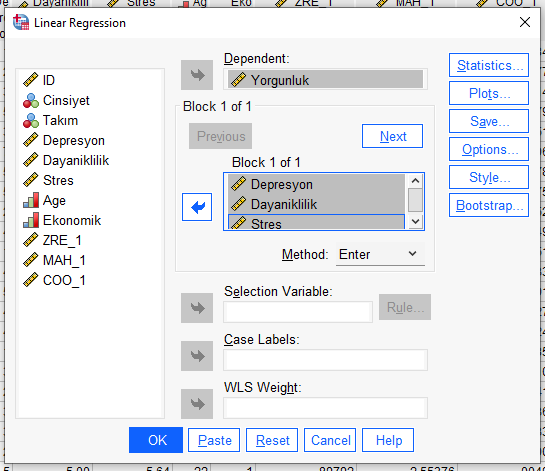
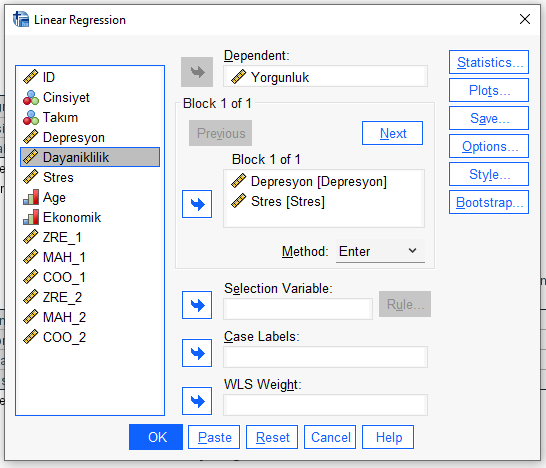
Bağımlı değişkenimizi Dependent kutusuna, bağımsız değişkenlerimizin hepsini tek seferde altındaki Independent(s) kutusuna atıyoruz. Method olarak Enter seçili olmalı.

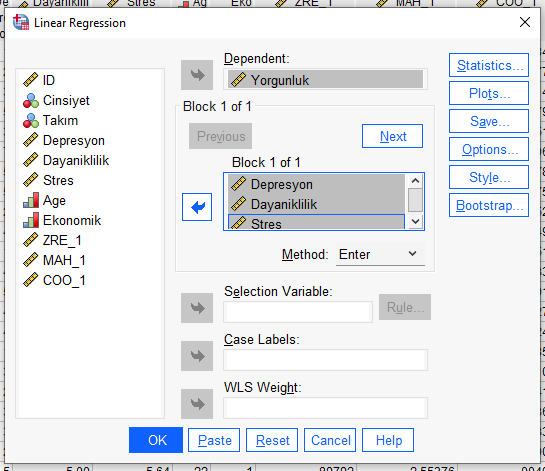
Daha sonra, “Statistics” butonuna basarak, açılan yeni pencerede, aşağıdaki kutucukları işaretliyoruz. Sonra “Continue”ya basıyoruz.

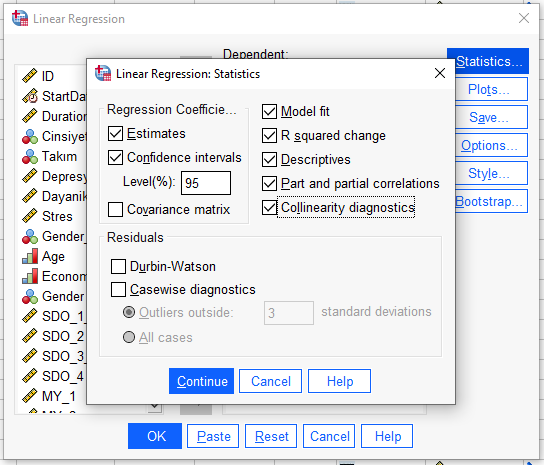
“Plots”a basıp, “Produce all partial plots” seçeneğini işaretliyoruz. “Continue”ya basıyoruz

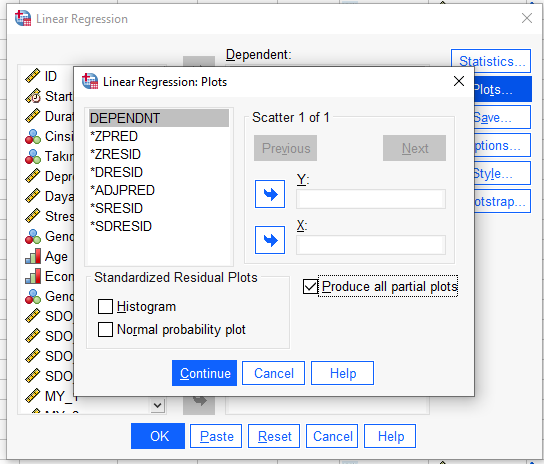
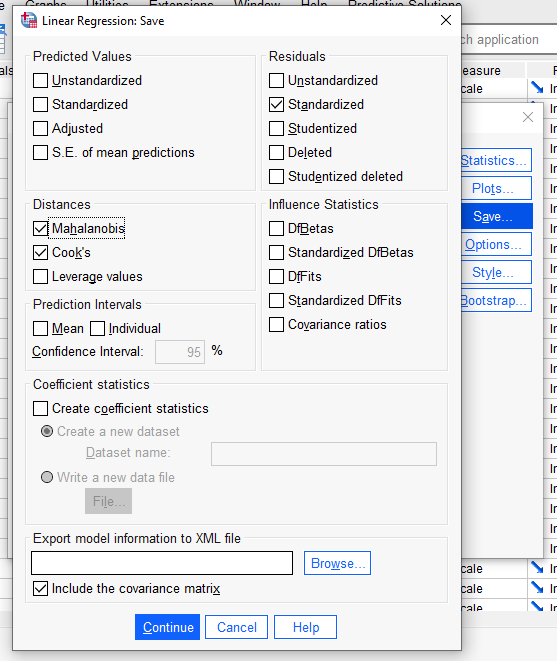
“Save” butonuna basıp, açılan yeni pencerede Mahalanobis, Cook’s (bu ikisi sadece uç değer bulmamıza yardımcı olacak) ve Standardized Residuals (bunun üzerinden daha sonra normal dağılımı da test edeceğiz) seçeneklerini işaretliyoruz.

“Continue”ya basıyoruz.

Son olarak, “OK” butonuna basarak SPSS’te forced entry çoklu regresyon analizimizi başlatıyoruz.

Forced Entry Çoklu Regresyon SPSS Tablo Yorumlama

Çoklu regresyon analizini başlattıktan sonra, SPSS bize bir sürü tablo verecektir. Bu tabloları nasıl okumamız gerektiğini ve önceki yaptığımız adımların üzerine varsayım testlerini nasıl yapacağımızı aşağıda anlatıyorum.

SPSS’in sonuç tabloları penceresinde önce, en alttaki “Charts” bölümüne bakmalıyız. Burada, teker teker her bağımsız değişkenin bağımlı değişkenle olan korelasyon ilişkisi hakkında tablolar bulunmakta. Bizim 3 bağımsız değişkenimiz olduğu için 3 tablo var.

İlk tablonun üzerine çift tıklıyoruz.

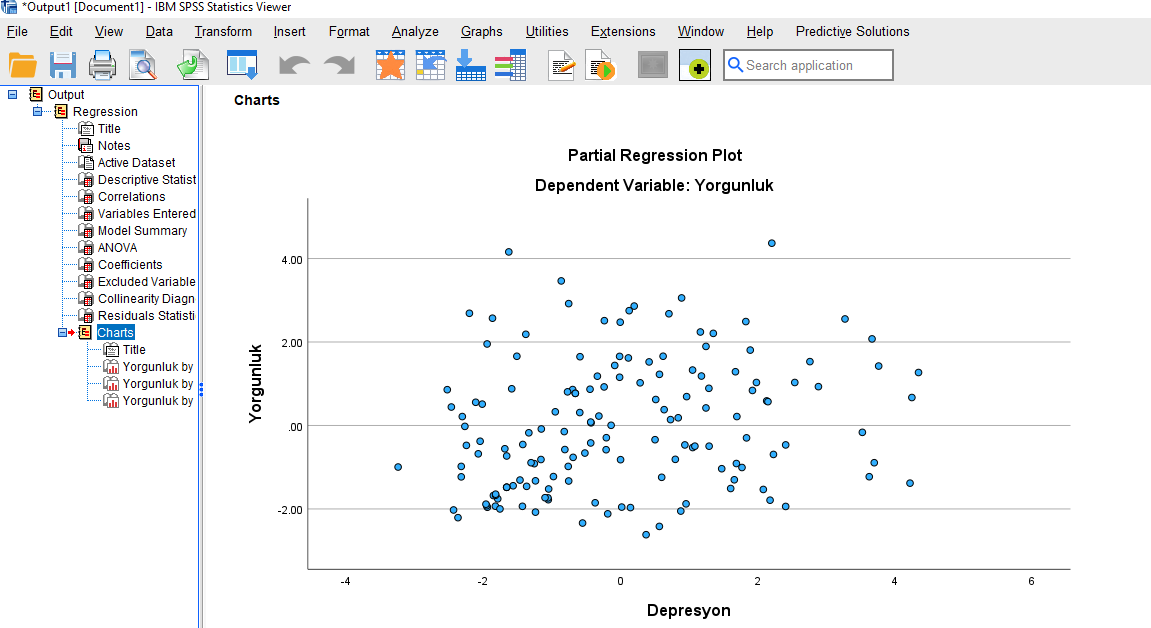
Açılan yeni pencerede sağ alttan beşinci minik ikona basıyoruz.

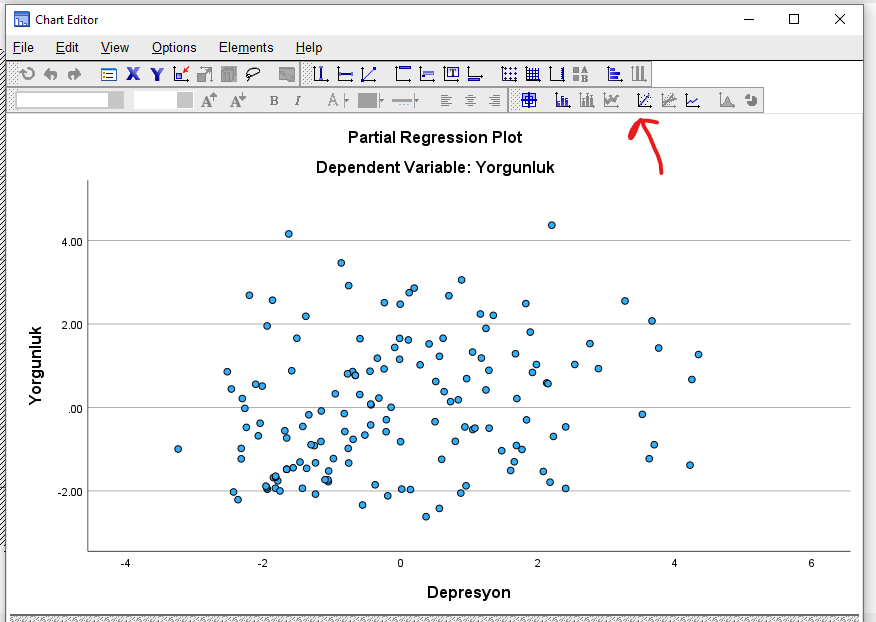
Bu bize bir korelasyon çizgisi verdi. Tabloyu gözümüzle inceliyoruz. Eğer doğrusal bir durum varsa, korelasyona devam ediyoruz.

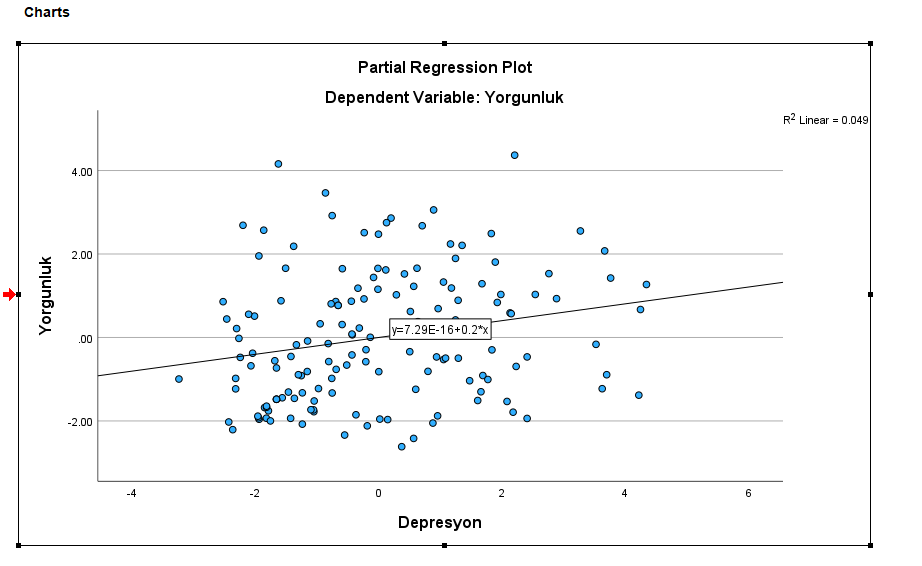
Aynı işlemi diğer iki grafik için de yapıyoruz.

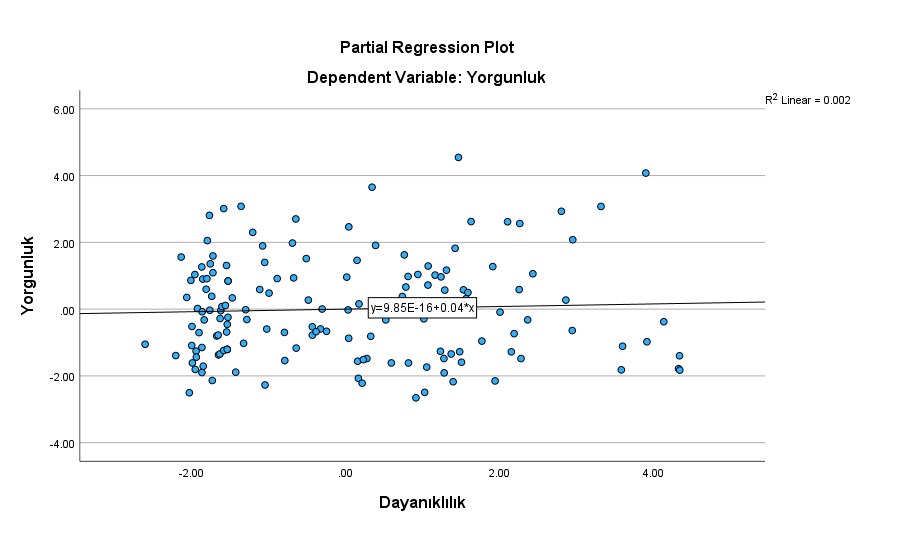
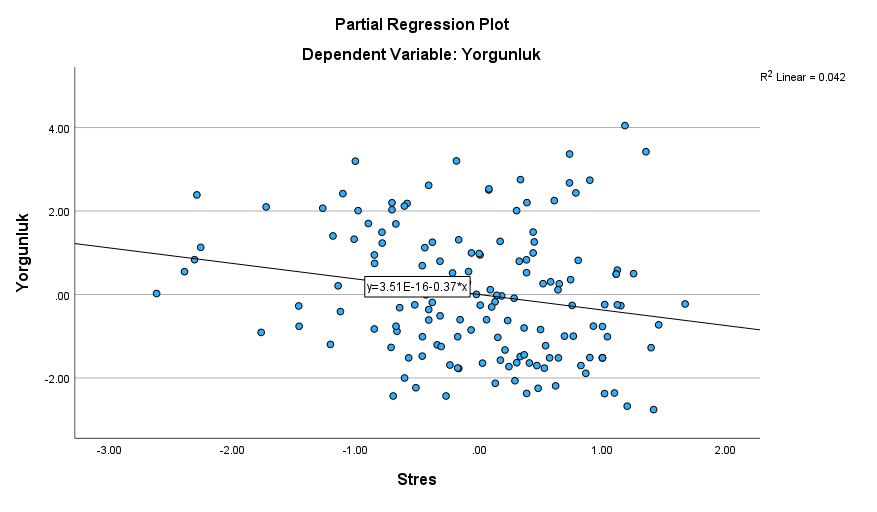
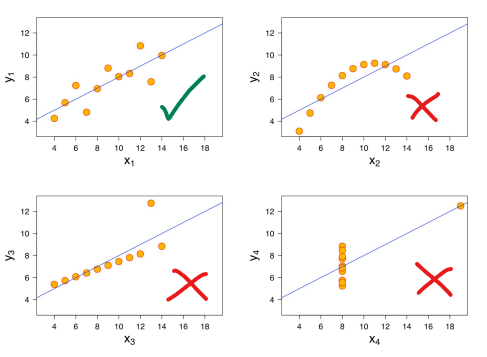
UYARI: Elde ettiğimiz grafiklerden herhangi biri, aşağıdaki resimde kırmızı çarpı işaretli grafiklere benzeseydi, bu, ilgili iki değişken arasında doğrusal ilişki olmadığı anlamına gelirdi.

Bir bağımsız değişkenin bağımlı değişkenle korelasyonu böyle bir grafik verdiyse, o bağımsız değişkeni çoklu regresyon analizinden çıkartıp, analizi aynı şekilde o değişken hariç en baştan yapmak daha doğru olacaktır.

Varsayım Kontrol: Uç Değer Bulma

Varsayımlarımızdan biri, verimizde uç değer olmamasıydı. Şimdi verideki uç değerleri nasıl buluruz onu inceleyeceğiz.

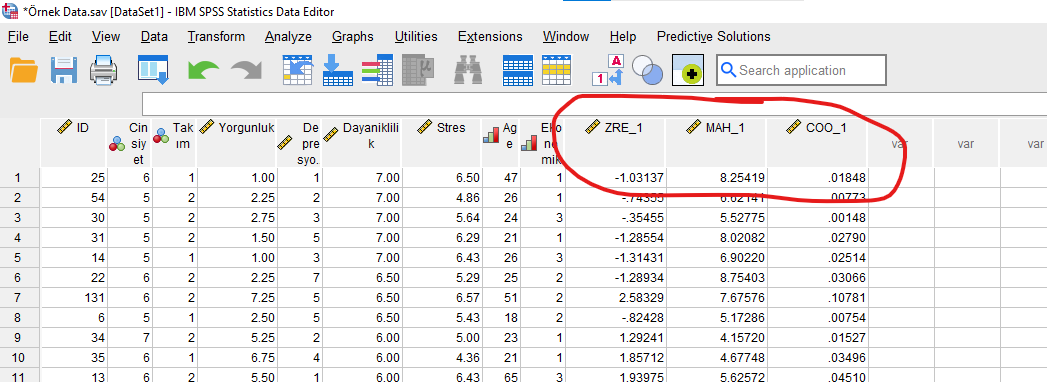
SPSS veri setimizin en sağ tarafında, SPSS’in bize 3 tane yeni değişken oluşturduğunu göreceğiz. Veri setimizdeki her katılımcının hangi değere sahip olduğunu tablodan inceleyebiliriz.

ZRE_1 = Standardized Residual demektir. -3 ve +3 değerleri dışındaki değerler uç değerlerdir. Eğer -3 ve +3 arasında olmayan bir Standardized Residual değerine sahip katılımcı varsa, o katılımcı veriden çıkartılıp, çoklu regresyon analizi aynı şekilde baştan tekrar yapılmalıdır.

MAH_1 = Mahalanobis Uzaklığı demektir. Bir değerin uç bir değer olduğunu gösteren Mahalanobis uzaklığı eşik değeri, veri setinin büyüklüğüne göre değişiyor. Basitçe yuvarlak bir hesap yöntemiyle:

• Örneklem büyüklüğümüz 500, 5 tane bağımsız değişkenimiz var ise => 25’ten büyük değerler problematik
• Örneklem büyüklüğümüz 100, 3 tane bağımsız değişkenimiz var ise => 15’ten büyük değerler problematik
• Örneklem büyüklüğümüz 30, 2 tane bağımsız değişkenimiz var ise => 11’den büyük değerler problematik

Problematik olan veriler, veri setinden çıkartılıp çoklu regresyon analizi en baştan tekrar yapılmalıdır. Veri setiniz yukarıdaki örneklere tam olarak uymuyorsa, bunların arasında göz kararı bir eşik değeri belirlemeye çalışın. Mahalanobis Uzaklığı hakkında daha detaylı bir yazıyı yine bu web sitesinde bulabilirsiniz.

COO_1 = Cook’s Distance demektir. +1 değerinden büyük Cook’s Distance değerleri uç değerlerdir. Eğer 1’den büyük bir Cook’s Distance değerine sahip katılımcı varsa, o katılımcı veriden çıkartılıp, çoklu regresyon analizi aynı şekilde baştan tekrar yapılmalıdır. Cook’s Distance hakkında daha detaylı yazımı okumak için linke tıklayın.

Varsayım Kontrol: Normal Dağılım Bulma

Forced entry çoklu regresyon varsayımlarımızdan ikincisi, verimizdeki Residual’ların normal dağılım göstermesiydi. Bu önemli bir varsayımdır. Bunu, SPSS’in bize oluşturduğu ZRE_1 yani Standardized Residual üzerinden test edeceğiz.

Analyze -> Descriptive Statistics -> Explore basıyoruz.

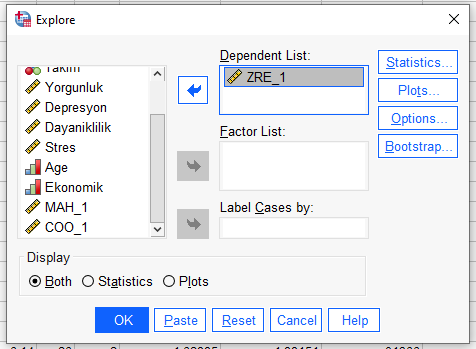
Açılan pencerede, ZRE_1 değişkenimizi Dependent List penceresine atıyoruz.

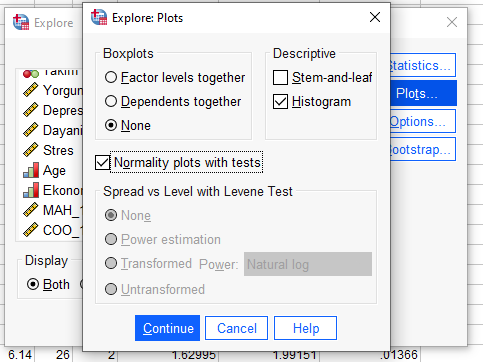
Plots’a basıp, aşağıdaki seçenekleri seçiyoruz.

Continue ve OK’a basıyoruz. SPSS bize yeni tablolar sunacak.

“Tests of Normality” tablosunda, Sig. değerlerine bakıyoruz. Shapiro-Wilk tarafındaki Sig. değerine bakmak genelde daha iyi. Bu tablodaki Sig. yani p değeri 0.05’ten büyükse, normallik varsayımı doğrulanmıştır diyebiliriz.

Eğer 0.05’ten küçükse ve diğer yöntemlerle de normal dağılım olduğunu doğrulayamıyorsak, çoklu regresyon yerine teker teker ikili non-parametrik (veya uygunsa parametrik) korelasyon analizleri yapmamız daha uygun olacaktır.

Eğer 0.05’ten küçük veya yakın bir değer çıktıysa, normallik testi ile normal dağılım olup olmadığına nasıl karar verebileceğimiz hakkında detaylı yazımı okumanızı öneririm.

Bu örnekte Sig. yani p değerlerinin ikisi de 0.05’in üzerinde, sorun yok.

Varsayım Kontrol: Çoklu Doğrusallık Bulma (Multicollinearity)

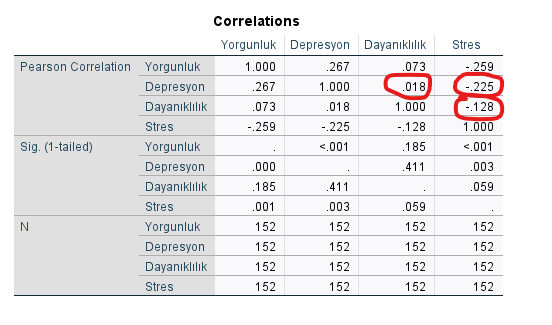
Bağımsız değişkenlerin ikisinin birbiriyle 0.70’ten fazla korelasyon göstermemesi gerekiyor demiştik. Bunu 2 tabloyu ayrı ayrı inceleyerek belirliyoruz.

“Correlations” tablosunda, bağımsız değişken çiftlerinin hepsi için Pearson Correlation miktarına bakıyoruz. Bu örneğimizde “Depresyon & Dayanıklılık”, “Depresyon & Stres” ve “Dayanıklılık & Stres” çiftlerinin Pearson korelasyon miktarlarının 0.70’ten büyük olmaması gerekiyor. Neyse ki hiçbiri büyük değil.

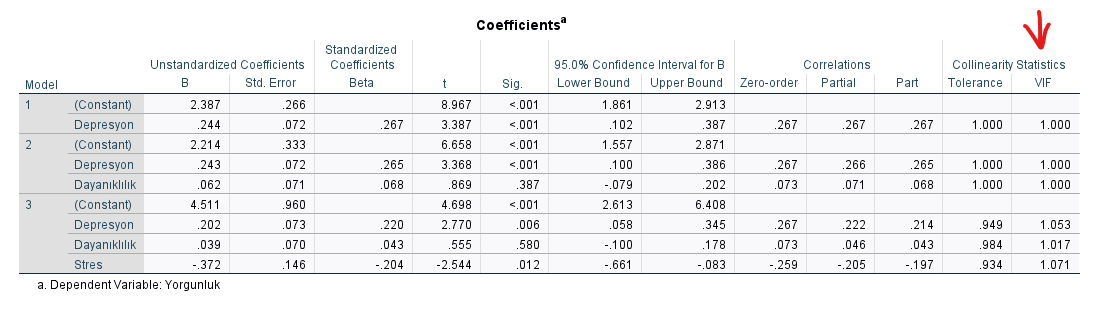
Çoklu doğrusallığı bir de Variance Inflation Factor (VIF) denen bir değer üzerinden test edebiliriz. Bunun için, SPSS tabloları arasından “Coefficients” başlıklı tablonun en sağdaki VIF isimli sütununa bakıyoruz.

Eğer değişkenlerden ikisinin VIF değerinin 10’dan büyük olduğunu görüyorsanız, o iki bağımsız değişken birbiriyle yüksek doğrusal korelasyona sahip demektir. Bu iki değişkenin bir tanesi veri setinden çıkartılıp, çoklu regresyon analizi o değişkensiz tekrar baştan yapılmalıdır.

Varsayımların hepsini buraya kadar yaptığımız işlemlerde test etmiş olduk. Buraya kadar yaptığımız varsayım testleri önemliydi, çünkü varsayımları doğrulamış olmamız çoklu regresyon analizinin sonuçlarının güvenilir olmasını sağlamaktadır.

Şimdi asıl forced entry metoduyla çoklu regresyon sonuçlarını incelemeye başlayalım.

3 tane bakmamız gereken tablomuz olacak. Bunlar regresyon modelinin istatistiksel olarak anlamlı olduğu, regresyon yönü, miktarı ve açıklama gücü hakkındadır.

ANOVA Tablosu

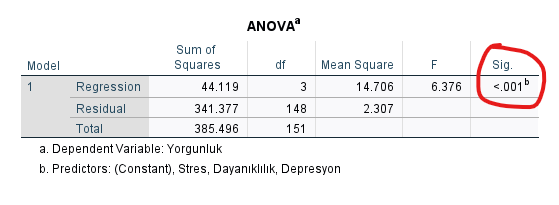
ANOVA tablosundaki Sig. değeri, p değeridir. Bu değer, SPSS’in kurduğu regresyon modelinin, rastgele bir dağılımdan anlamlı şekilde farklı olup olmadığını belirlemeye yarar. Eğer p değeri 0.05’ten küçükse, bağımsız değişkenlerden en az 1 tanesinin bağımlı değişken ile arasında anlamlı bir korelasyon ilişkisi var demektir.

Bu tablodaki p değeri bütün bağımsız değişkenlerin birlikte modele sokulmasıyla yapılan regresyon analizinin anlamlılık değeridir. Eğer bu değer 0.05’in altında ise, regresyon modelimiz istatistiksel olarak anlamlı demektir.

Bu örnekte 0.05’in altında bir p değeri bulduk. Yani Stres, Dayanıklılık ve Depresyon değişkenlerinden en az 1 tanesi, Yorgunluk bağımlı değişkeni üzerinde etkiye sahipmiş.

Model Özeti

“Model Summary” tablosundaki Adjusted R Square değeri, modelin bağımsız değişkenlerinin bağımlı değişken üzerindeki değişimi açıklama gücünü ifade eder. Bu örnekte 0.096 çıkmış, yani modeldeki değişkenler, Yorgunluk üzerindeki değişimin %9.6’sını açıklayabiliyor. Yorgunluk üzerindeki kalan %90.4’lük değişim, bu modelde olmayan bilinmeyen başka faktörlere bağlıdır.

Regresyon Korelasyon Miktarları

“Coefficients” tablosundaki Sig. değerleri, her bağımsız değişkenin ayrı ayrı bağımlı değişkenle olan ilişkisinin p anlamlılık değerini gösterir. Bu tabloya göre Depresyon, Yorgunluk ile anlamlı bir ilişkiye sahipmiş (çünkü p değeri 0.006 yani 0.05’ten küçük). Dayanıklılık, Yorgunluk ile anlamlı bir ilişkiye sahip değilmiş. Stres de Yorgunluk ile anlamlı bir ilişkiye sahipmiş.

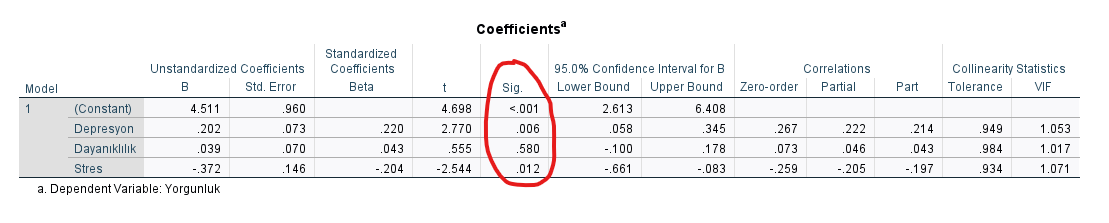
Ek Bilgi: Bu tabloda Correlations bölümündeki Partial, kısmi korelasyonu (yani o satırdaki bağımsız değişkenin bağımlıya etkisi modele tamamen dahil, diğer bağımsız değişkenlerin kendi başlarına etkileri modelin dışında), Part da (semi-partial) yarı-kısmi korelasyonu (yani o satırdaki bağımsız değişkenin bağımlıya sadece kendi başına etkisi modele dahil, diğer bağımsız değişkenlerin etkileri modelin tamamen dışında) göstermektedir.

Tekrar SPSS’te Forced Entry Regresyon (Sadece Anlamlı Bağımsız Değişkenlerle)

İlk başta test ettiğimiz modelde 3 tane bağımsız değişken vardı: Depresyon, Dayanıklılık, Stres. Yukarıda yaptığımız forced entry regresyon analizinde bunlardan sadece Depresyon ve Stres’in bağımlı değişken olan Yorgunluk ile ilişkisi olduğunu bulduk. Şimdi, bir forced entry regresyon daha yapmamız gerekiyor, bu sefer sadece anlamlı olan değişkenlerle (yani Depresyon ve Stres). Bu adım öncekilere göre baya kısa sürecek.

Yine Analyze -> Regression -> Linear basıyoruz.

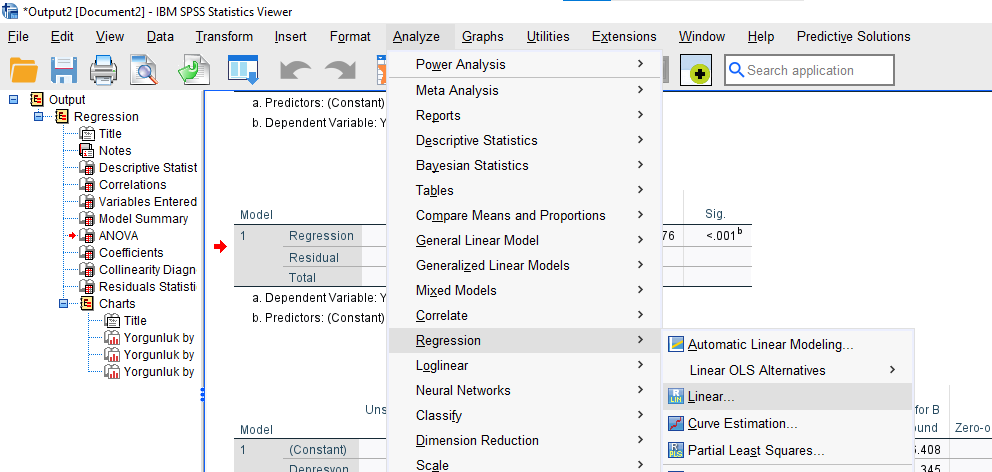
Dayanıklılık değişkenini analiz kutusundan çekip soldaki kutuya geri atıyoruz. Başka hiçbir değişiklik yapmadan “OK”a basıyoruz ve analizi başlatıyoruz.

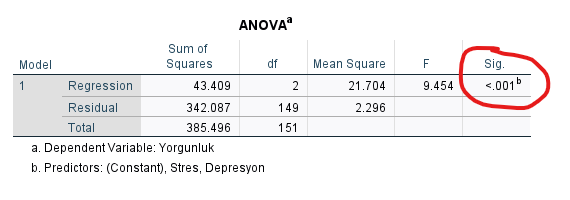
Tablolardan ANOVA tablosundaki Sig. değeri 0.001’den küçük. Demek ki 2 bağımsız değişkenli yeni regresyon modelimiz hâlâ istatistiksel açıdan anlamlı.

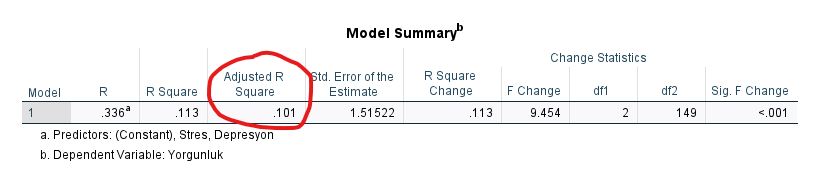
“Model Summary” tablosundaki Adjusted R Square değeri, modelin bağımsız değişkenlerinin bağımlı değişken üzerindeki değişimi açıklama gücünü ifade eder. Bu yeni regresyon analizi tablosunda 0.101 çıkmış (eskisi 0.096’ydı), yani modeldeki değişkenler, Yorgunluk üzerindeki değişimin %10.1’sını açıklayabiliyor. Demin 3 değişkenle yaptığımız ilk forced entry regresyon analizindeki model, Yorgunluk üzerindeki değişimin %9.6’sını açıklıyordu. Yeni yaptığımız 2 değişkenli regresyon modeli, Yorgunluk üzerindeki değişimi daha iyi açıklamış.

En son modelimiz Yorgunluk üzerindeki değişimin %10.1’sını açıklayabiliyor demiştik. Yorgunluk’taki kalan %89.1’lik değişim, bu modelde olmayan bilinmeyen başka faktörlere bağlıdır.

“Coefficients” tablosundaki Sig. değeri yani p değeri, her bağımsız değişkenin, bağımlı değişkendeki değişim üzerinde önemli bir etkisi olup olmadığı bilgisini verir. Eğer p değeri 0.05’ten küçük ise anlamlı demektir. Bu tabloya göre Depresyon ve Stres, bağımlı değişken olan Yorgunluk üzerinde anlamlı bir değişime sebep olmaktadır (çünkü p değerleri sırayla 0.006 ve 0.009).

B değeri, her bağımsız değişkenin ölçüldüğü ölçekteki 1 birimlik değişimin, bağımlı değişken üzerinde kaç birimlik değişime sebep olduğunu söylüyor. Örneğin Depresyon’daki 1 birimlik değişim, Yorgunluk’ta 0.201 miktarda bir artışa sebep oluyor. Stres’teki 1 birimlik değişim, Yorgunluk’ta 0.382 miktarda azalışa sebep oluyor.

Beta ise, farklı değişkenlerin ölçeklerinin standardize edilmesiyle bulunan bir değerdir. Burada, değerlerin kendisi değil de standart sapmaları üzerinden bir yorumlama yapılmaktadır. Beta değerleri şöyle okunur: “Depresyondaki değerde 1 standart sapmalık artış, Yorgunlukta 0.219 standart sapmalık artışa sebep olur; Stresteki 1 standart sapmalık artış, Yorgunlukta 0.209 standart sapmalık azalışa sebep olur”.

Son olarak, modelimizdeki hangi bağımsız değişkenlerin bağımlı değişkene ne kadar etki ettiğini bulmak için Coefficients tablosundaki Part sütununa bakıyoruz.

Part değerinin karesini alıp sonra onu yüzde cinsinden yazarsak, o bağımsız değişkenin, tek başına bağımlı değişkendeki değişimi yüzde kaç açıkladığını öğreniyoruz.

Bu örnekte Depresyon’un Part değeri 0.214. Karesini alırsak 0.046 ediyor. Yani Depresyon, Yorgunluk’taki değişimin %4.6’sını açıklıyormuş.

Benzer şekilde Stres’in Part değeri -0.204. Karesini alırsak 0.041 ediyor. Yani Stres, Yorgunluk’taki değişimin %4.1’ini açıklıyormuş.

Forced entry metoduyla çoklu doğrusal regresyon yapma adımları bu kadardı. Önce bütün değişkenleri aynı anda modele sokarak regresyon modelini kurup bağımlı değişkene etki etmeyen değişkenleri çıkartıp tekrar regresyon modeli kuruyoruz ve sonunda her bağımsız değişken bağımlı değişkeni nasıl etkiliyor diye bakıyoruz. Artık regresyon analizi yapıp sonuçları öğrendiğimize bu analizin raporlamasını yapabiliriz.