SPSS ile Mann Whitney U Testi (Resimli)

Bu sayfada, Mann Whitney U testinin ne olduğundan kısaca bahsedeceğiz ve SPSS programını kullanarak nasıl Mann Whitney U testi yapıldığını göstereceğim.

Mann Whitney U Testi Nedir?

Mann Whitney U Testi, birbirinden farklı kişilerden oluşan 2 tane grubun ortalama skorlarını karşılaştırmak için kullanılır. Bu testin bağımsız örneklem t testinden farkı, parametrik olmayan bir test olmasıdır. Yani t testinin normallik varsayımını karşılayamadığımız durumda t testine alternatif olarak yapılır. Aynı zamanda, bağımlı değişkenin veri tipinin ordinal veri tipi olduğu durumlarda da Mann Whitney U Testi yapılır.

Mann Whitney U Testi, aynı zamanda “Wilcoxon rank-sum test” veya “Mann Whitney Wilcoxon Test” olarak da isimlendirilir. Bu testlerin hepsi aynı testtir.

Mann Whitney U Testi Varsayımları

Mann Whitney U Testi yapmak için verinin normal dağılıma sahip olması gerekmez. Fakat, gruplardaki kişi sayısının eşit olması ve varyansların homojen olması iyi olur. Aksi takdirde, Mann Whitney U Testi sonuçları yanıltıcı olabilir.

Eğer veride hem varyans homojenliği sağlanmıyorsa hem de gruplardaki kişi sayıları arasında %40 veya daha fazla fark varsa o zaman grupları karşılaştırmak için Medyan Testi yapmak Mann Whitney U Testi’nden daha doğru sonuçlar verebilir.

SPSS ile Mann Whitney U Testi Nasıl Yapılır?

SPSS’te şu adımları izleyerek Mann Whitney U Testi’ni yapabiliriz:

Adım 1:

Öncelikle, SPSS’te Analyze -> Nonparametric tests -> Legacy Dialogs -> 2 Independent Samples butonlarına tıklıyoruz.

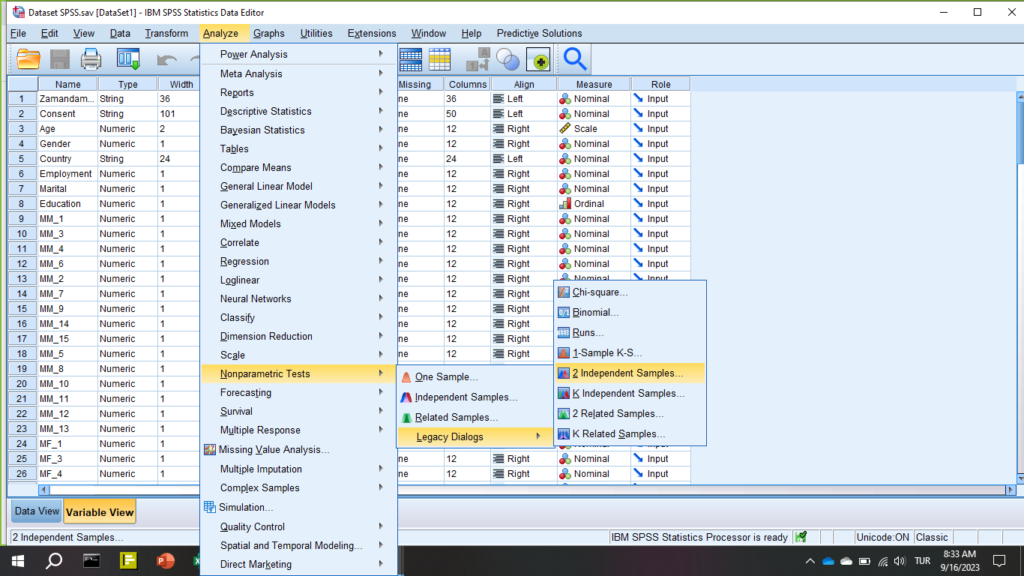
Adım 2:

Sonra, sol bölümden bağımsız değişkenimizi bulup Grouping Variable kısmına atıyoruz ve bağımlı değişkenimizi Test Variables kısmına atıyoruz. Teste devam edebilmemiz için Grouping Variable’ın altındaki Define Groups butonuna tıklamamız gerekiyor.

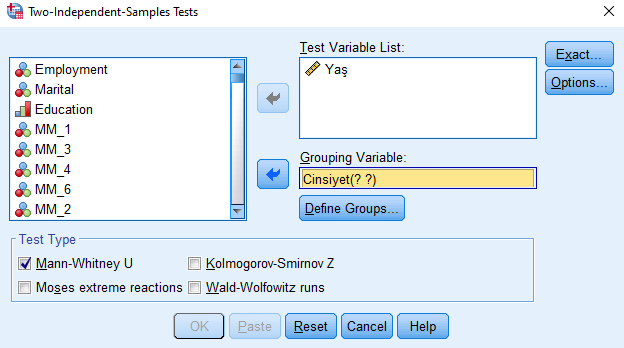
Adım 3:

Karşılaştırmak istediğimiz iki grubun hangi gruplar olduğunu SPSS’te hangi sayılarla kaydettiysek bu penceredeki boşluklara o sayıları yazıyoruz. Hangi sayılarla kaydettiğinizi bilmiyorsanız Değişkenlerin Hangi Değerlerle Kaydedildiğini Görme başlıklı yazımıza bakıp hızlıca öğrenebilirsiniz.

Bunu yaptıktan sonra Continue tuşuna basıyoruz.

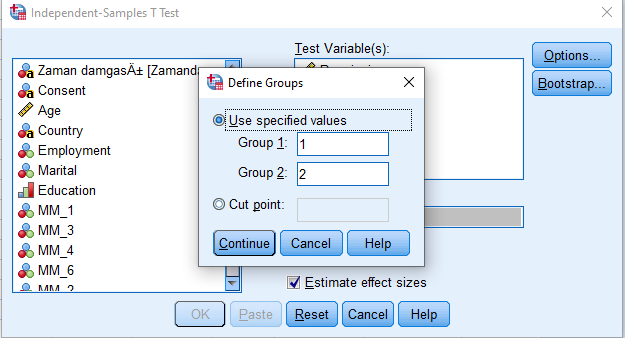
Adım 4:

Artık Grouping Variable bölümündeki parantezlerin içinde sayılar var. Şimdi OK tuşuna basıp analiz sonuçlarını görebiliriz.

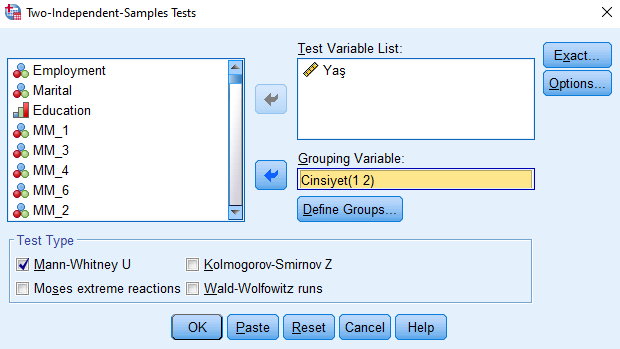
Mann Whitney U Testi Yorumlama

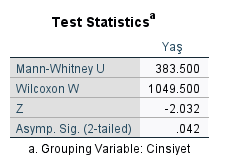
Mann Whitney U Testi’ni başlattıktan sonra SPSS önümüze tablolar getirecektir. Bu tablolardan öncelikle Test Statistics tablosundaki en alt satırda Sig. değerine (yani p değeri) bakmak gerekiyor. Bu değer 0.05’ten küçük ise, iki grubun ortalamaları arasında anlamlı bir fark vardır sonucuna ulaşabiliriz. Bu değer 0.05’ten büyük ise, iki grubun ortalamaları arasında anlamlı bir fark yoktur diyebiliriz.

Örneğimizde, p değeri 0.042 çıkmış, yani 0.05’ten küçük. Şimdi hangi grubun ortalamasının daha yüksek olduğunu öğrenmek için Ranks tablosuna bakmamız gerekiyor. Ranks tablosundaki Mean Rank sütununa göre, Erkek katılımcıların ortalama yaşı Kadın katılımcılardan daha yüksek.

Dikkat!

Ranks tablosundaki Mean Rank, grupların gerçek ortalamasını vermiyor. Bir veri setindeki bir değişkene ait iki grubun (mesela kadın ve erkek) gerçek ortalamalarını ayrı ayrı bulmak için, İki Grubun Ortalamalarını Ayrı Ayrı Bulma başlıklı yazımıza göz atabilirsiniz.

Mann Whitney U Testi Etki Büyüklüğü Bulma

Yaptığımız Mann Whitney U Testi’nin sonucunda eğer anlamlı bir fark bulduysak, etki büyüklüğünü de raporlamamız faydalı olacaktır. Mann Whitney U Testi için etki büyüklüğü hesaplamak oldukça kolaydır. [Z / √(n)] formülüne göre Mann Whitney U Testi etki büyüklüğü hesaplanabilir.

Yani, Z değerini örneklem büyüklüğünün kareköküne bölmemiz yeterlidir. Bu örnekte hemen yukarıdaki tabloya bakarsak Z değerinin -2.032 olduğunu görebiliriz. Veri setinde 67 katılımcı vardı. Formülde yerine yerleştirirsek, [-2.032 / (√(67) = -0.248] olarak etki büyüklüğünü -0.248 buluyoruz. Değerin negatif ya da pozitif olması fark etmiyor, 0’a olan uzaklığı önemli.

Mann Whitney U Testi etki büyüklüğü yorumlama için de şu değer aralıkları kullanılmaktadır: 0.1 (küçük etki), 0.3 (orta etki), 0.5 ve üstü (büyük etki).

O zaman bizim örneğimizde bulduğumuz -0.248 değerinin orta etki büyüklüğüne yakın olduğunu söyleyebiliriz.