Temel Bileşen Analizi (SPSS) — Resimli

Temel Bileşen Analizi, çok değişkenli veri setlerinin boyutunu azaltmak için kullanılan istatistiksel bir tekniktir. Bu yöntemde, veri setindeki değişkenler arasındaki varyansın büyük bir kısmını temsil eden ve birbirleriyle mümkün olduğunca az korelasyona sahip olan yeni bileşenler bulunmaya çalışılır (her bileşenin içinde birçok değişken bulunur). Bu analiz, veri setindeki karmaşıklığı azaltarak veri analizi sürecini daha anlaşılır hale getirir ve değişkenler arasındaki yapısal ilişkileri anlamak için bir ön adım olarak kullanılır. Bu yazıda, Temel Bileşen Analizi nedir, SPSS programı ile nasıl yapılır ve sonuçları nasıl yorumlanır konularını ele alacağız.

Temel Bileşen Analizi Nedir?

Temel Bileşen Analizi (Principal Component Analysis = PCA), istatistiksel bir yöntem olup, çok değişkenli veri setlerini daha az değişkenli bir forma dönüştürmek için kullanılan bir boyut indirgeme tekniğidir. Bu analiz, veri setindeki değişkenler arasındaki ilişkileri anlamak ve veri setinin karmaşıklığını azaltmak amacıyla kullanılır. Genellikle veri setindeki varyansın büyük bir kısmını korurken daha küçük bir boyuta indirgeme hedeflenir.

Temel Bileşen Analizi, veri setindeki değişkenler arasındaki korelasyonları dikkate alarak yeni bir değişken seti oluşturur. Bu yeni değişkenler, orijinal veri setindeki değişkenler arasındaki en yüksek varyansı içerir. Temel Bileşen Analizi adı verilen bu yeni değişkenler, veri setinin boyutunu azaltırken, veri setindeki varyansın büyük bir kısmını korur.

Temel Bileşen Analizi, birçok farklı alanda kullanılan yaygın bir istatistiksel tekniktir. Özellikle, veri görselleştirme, boyut indirgeme, veri sıkıştırma ve veri analizi gibi alanlarda sıklıkla kullanılır. Ayrıca, veri setlerindeki karmaşıklığı azaltarak, daha kolay yorumlanabilir sonuçlar elde etmek için de tercih edilir. Bu analiz, özellikle büyük ve karmaşık veri setleriyle çalışırken çok değerli bir araçtır.

Maksimum Varyansın Açıklanması Neden Önemlidir?

Temel Bileşen Analizi’nde (PCA’da), verilerdeki maksimum varyansı açıklayan bileşenleri çıkarmanın amacı, verilerdeki mümkün olduğunca fazla değişkenliği yakalayan orijinal değişkenlerin (temel bileşenler olarak bilinir) bir dizi ortogonal doğrusal kombinasyonunu bulmaktır. Bu, orijinal değişkenlerin doğrusal olarak ilişkisiz ve açıkladıkları varyans miktarı açısından sıralı yeni bir değişkenler kümesine (temel bileşenler) dönüştürülmesiyle elde edilir.

PCA’da varyansın maksimize edilmesinin ardındaki mantık, en yüksek varyansa sahip değişkenlerin veri kümesi hakkında en fazla bilgiyi içeren değişkenler olduğu fikrine dayanmaktadır. Varyansın en büyük oranını açıklayan bileşenleri koruyarak PCA, mümkün olduğunca fazla bilgiyi korurken verilerin boyutluluğunu etkili bir şekilde azaltır.

Pratik anlamda, PCA’da çıkarılan bileşenler açıkladıkları varyans miktarına göre sıralanır; birinci bileşen en fazla varyansı açıklar, ikinci bileşen ikinci en fazla varyansı açıklar ve bu böyle devam eder. Araştırmacılar genellikle verilerdeki toplam varyansın yüksek bir yüzdesini toplu olarak açıklayan belirli sayıda temel bileşeni tutmayı tercih eder. Bu, bilgi kaybını en aza indirirken boyutluluğun azaltılmasını sağlar.

Genel olarak, PCA’da varyansı en üst düzeye çıkarmanın amacı, en önemli kalıpları veya varyasyon kaynaklarını belirleyerek verilerin kompakt bir temsilini sağlamak ve veri kümesinin altında yatan yapıyı anlamayı ve yorumlamayı kolaylaştırmaktır.

Temel Bileşen Analizi Varsayımları Nelerdir?

Temel Bileşen Analizi (PCA) yöntemi kullanılmadan önce bazı önemli varsayımların sağlanması gerekir. Bu varsayımlar, PCA’nın doğru bir şekilde uygulanması ve sonuçların güvenilir olması için önemlidir. Temel Bileşen Analizi’nin temel varsayımları şunlardır:

1. Doğrusallık: PCA, değişkenler arasındaki ilişkilerin doğrusal olduğunu varsayar. Bu, değişkenler arasındaki ilişkinin doğrusal bir yapıya sahip olduğu durumlarda PCA’nın uygun olduğu anlamına gelir. Eğer ilişkiler doğrusal değilse, PCA’nın sonuçları yanıltıcı olabilir.
2. Bağımsızlık: PCA, değişkenler arasında bağımsızlık varsayımını gerektirir. Bu, herhangi bir değişkenin diğer değişkenlerden bağımsız olarak ölçülmüş olması gerektiği anlamına gelir. Yani değişkenler arasında biraz korelasyon olması istense de, çok fazla yüksek korelasyonlar da bulunmamalıdır.
3. Normallik: PCA’nın doğru bir şekilde uygulanması için değişkenlerin normal dağılıma sahip olması tercih edilir. Ancak, PCA’nın normallik varsayımı kesinlikle zorunlu değildir. Normallik varsayımının sağlanmaması durumunda, PCA sonuçlarına dair güven düzeyi düşebilir, ancak analizin genellikle yeterince sağlam olabileceği belirtilir.

Bu varsayımların sağlanması, PCA’nın doğru bir şekilde uygulanması ve sonuçların güvenilir olması için önemlidir. Ancak, pratikte bazı varsayımların tam olarak sağlanmaması durumunda bile PCA kullanılabilir, ancak sonuçların yorumlanmasında daha dikkatli olunması gerekebilir.

SPSS ile Temel Bileşen Analizi Nasıl Yapılır?

SPSS kullanarak Temel Bileşen Analizi’ni aşağıdaki adımları izleyerek yapabiliriz. Aşağıda hem adım adım ne yapmak gerektiğini göstereceğim, hem de hangi adımdaki değişik seçenekler ne anlama geliyor onu anlatacağım.

Temel Bileşen Analizi, bir Faktör Analizi yöntemi olmasa da, SPSS’te Factor Analysis penceresinden yapılmaktadır. Bu ikisi arasındaki farkı anlatan yazımı okumak için linke tıklayabilirsiniz.

Analyze -> Dimension Reduction -> Factor butonlarına basıyoruz.

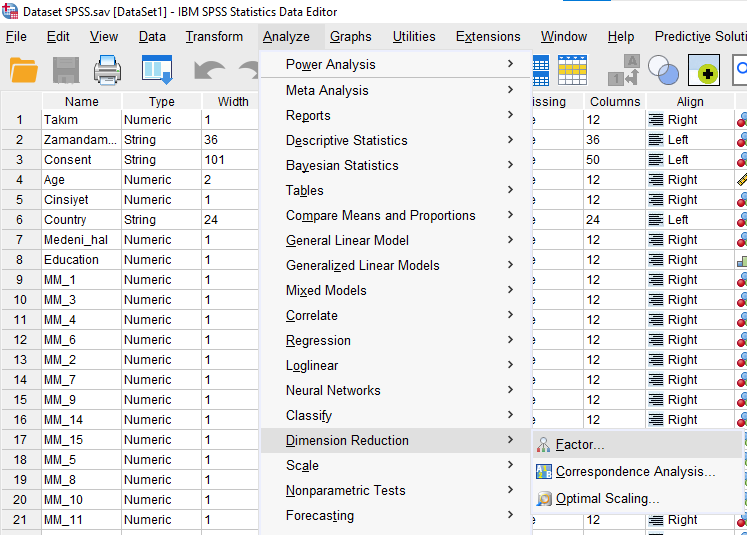
Açılan Factor Analysis penceresinde, temel bileşen analizi yapacağımız bütün maddeleri Variables kutusuna atıyoruz. Genellikle temel bileşen analizini yapma sebebimiz, bir ölçek setindeki birçok ölçeğin açıkladığı varyansın mümkün olduğunca çok miktarını, ölçeklerin gruplandırılmasıyla oluşturulan daha az sayıda yeni temel bileşen ile açıklamaktır. Bu sayede veri setindeki yapıları ve ilişkileri daha iyi anlarız. Bu yüzden genelde temel bileşen analizi değişkenleri, bir anketin sorularının tamamıdır.

Bu örnekte de MM isimli bir ölçeğin sorularının hepsini Variables kutusuna attık. Temel Bileşen Analizi kullanarak, acaba MM ölçeğinin sorularındaki en yüksek varyansı en düşük bileşen sayısıyla nasıl açıklayabiliyoruz diye bakacağız.

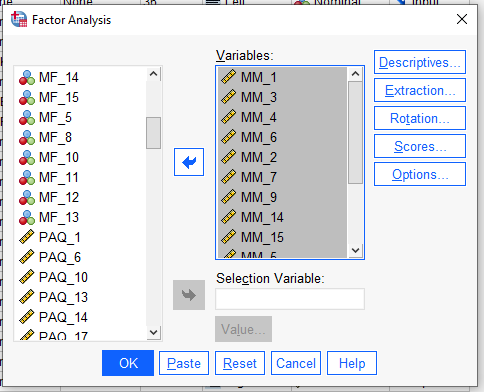
“Descriptives” butonuna basarak, aşağıdaki resimde işaretli olan seçeneklerin hepsini işaretliyoruz. Bartlett’s Test Of Sphericity bunların en önemlisi, bu test değişkenlerin birbirleriyle lineer ilişki durumunu ölçecek. Buna daha sonra değineceğiz.

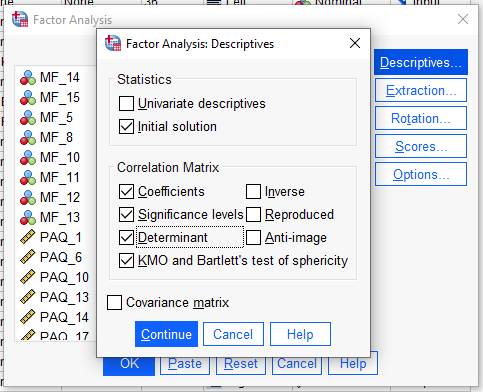
“Extraction” butonuna basarak yeni bir pencere açıyoruz. Burada vermemiz gereken bir sürü karar var. Bunlara göre SPSS’in temel bileşen analizimizi nasıl yapacağı değişecek.

Method

Method menüsünden, Principal Components seçeneğini seçmeliyiz. Bu, SPSS’te Factor Analysis penceresinde yapıyor olduğumuz analizin Faktör Analizi değil de Temel Bileşen Analizi olmasını sağlar.

Analyze

Daha sonra, Analyze bölümünden Correlation Matrix veya Covariance Matrix’ten birini seçmeliyiz. Eğer temel bileşen analizine soktuğunuz soruların hepsi aynı ölçekte ise (mesela hepsi 1 ile 7 arasında ölçülüyorsa) hangi Analyze seçeneğini seçtiğiniz fark etmez. Fakat eğer farklı ölçekteki soruları (mesela bir soru 1-5 arasında, diğer soru 1-7 arasında şıklar içeriyorsa) o zaman mutlaka Correlation Matrix seçmek gerekir.

Extract

Extract bölümünde, temel bileşen analizi sonucunda kaç grup olacağına dair bir seçim yapıyoruz. Based On Eigenvalue seçersek, temel bileşen analizi sonucunda kaç bileşen olacağını SPSS’e bırakmış oluyoruz. SPSS analiz edilen sorular farklı kombinasyonlarda gruplar ve Eigenvalue’su 1’in üzerinde olan bir kombinasyon SPSS tarafından bir temel bileşen olarak belirlenir.

Fixed Number Of Factors seçersek, SPSS’e, bizim analiz ettiğimiz soruları kaç farklı temel bileşen içinde gruplamasını istediğimizi söylüyoruz.

Display

Display başlığı altındaki 2 seçeneği de işaretlersek temel bileşen analizi sonuçlarına daha kapsamlı bir bakış açımız olacak.

Maximum Iterations For Convergence

Bunu 25’in üstünde yaparsak analizin yapılmasını bekleme süremiz artabilir ve bilgisayarımız kasabilir. 25 iterasyon genellikle SPSS’in isabetli bir model oluşturup bize isabetli bir temel bileşen analizi sonucu vermesi için yeterli bir miktardır.

“Rotation” butonuna basarak hangi rotasyonu kullanacağımızı seçeceğiz. Bu metotlardan Varimax, Quartimax ve Equamax orthogonal rotasyonlardır. Analiz sonucu oluşturacağımız az sayıdaki temel bileşenlerimiz arasında bir ilişki beklemiyorsak orthogonal rotasyonlardan birini seçmeliyiz. Direct Oblimin ve Promax ise oblique rotasyonlardır. Temel bileşenlerimiz arasında bir ilişki bekliyorsak oblique rotasyonlardan birini seçmeliyiz. Temel Bileşen Analizi için Varimax ve Direct Oblimin, en sık seçilen rotasyonlardır.

Varimax = Analiz edilen soruları olabildiğince çok temel bileşene ayırır. Orthogonal rotasyondur.

Quartimax = Analiz edilen soruları olabildiğince az temel bileşene ayırır. Orthogonal rotasyondur.

Equamax = Varimax ve Quartimax’ın arasıdır. Orthogonal rotasyondur.

Direct Oblimin = Az sayıda katılımcıyla daha iyi çalışan oblique rotasyondur. Sosyal bilimlerde genelde bu seçilir.

Promax = Binlerce katılımcımız varsa daha daha iyi çalışan oblique rotasyondur.

Bu örnekte, gözlemlediğimiz veri setinde oluşturulacak olan temel bileşenler arasında bir ilişki beklemiyoruz. Bu yüzden “Varimax” rotasyon metodunu seçiyorum. Siz kendi veri setinizle analizinize göre farklı bir rotasyon metodu seçebilirsiniz.

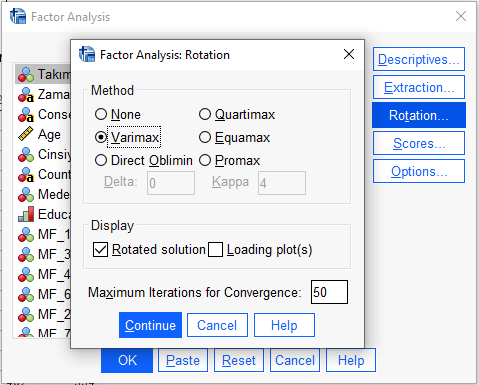
“Options” butonuna basarak açılan pencerede “Missing Values” bölümünde eksik verileri ne yapacağımızı seçiyoruz.

Exclude Cases Listwise = Eğer bir katılımcı temel bileşen analizini yaptığımız soruların (ya da ölçeklerin) en az 1 tanesini cevaplamamışsa, katılımcı temel bileşen analizinden tamamen çıkartılır.

Exclude Cases Pairwise = Eğer bir katılımcı temel bileşen analizini yaptığımız soruların (ya da ölçeklerin) bazılarını cevaplamamamış bazılarını cevaplamışsa, katılımcının cevapladığı sorular temel bileşen analizine dahil edilir.

Replace With Mean = Katılımcıların cevaplamadığı sorular / ölçekler, ortalama değer ile doldurulur. Bunun kullanılması önerilmez.

“Coefficient Display Format” bölümünde temel bileşen analiz sonuçlarını tablolar üzerinde nasıl göreceğimizi belirleyeceğiz.

Sorted By Size = İçinde en çok sayıda soru bulunan temel bileşen, tabloda en üstte gösterilir. En az sayıda soruyu barındıran temel bileşen de en altta gösterilir.

Suppress Small Coefficients = Temel Bileşen Analizi tablosunda belirli bir değerden küçük bileşen yüklerinin görünmemesini sağlar. Bileşen yükleri hâlâ tabloda bulunur ama bize görünmez. Bu, daha temiz bir temel bileşen analizi tablosu görmemizi sağlar. Temel bileşen analizi tablosunu en kolay görmemizi sağlayan en ideal değer 0.30’dur. Bu yüzden burada 0.30 yazarsak daha iyi görürüz.

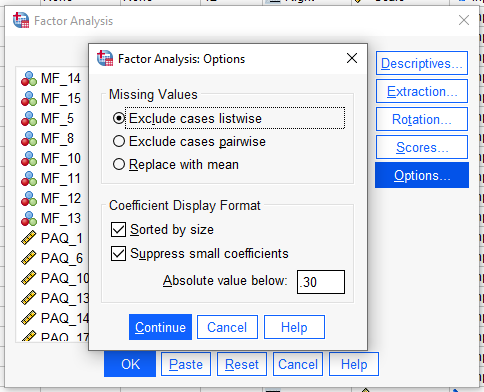
Buraya kadar bütün ayarlamaları yapmış olduk. Continue ve OK’a basarak SPSS’in Temel Bileşen Analizi’mizi başlatmasını sağlayalım.

Temel Bileşen Analizi Yorumlama

Temel Bileşen Analizi sonucunda SPSS birtakım tablolar sunacaktır. Bu tabloların önemli olanlarına bakalım şimdi.

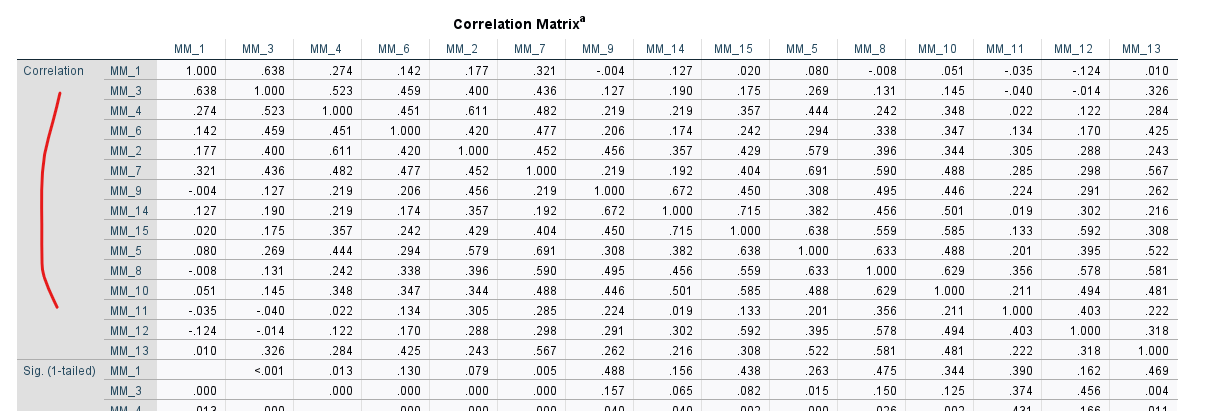
İlk olarak “Correlation Matrix” başlıklı tabloya bakıyoruz. Burada, temel bileşen analizi yaptığımız soruların birbirleriyle olan korelasyonlarını inceleyeceğiz. Sorular birbirleriyle bir miktar pozitif korelasyon göstermeli ama 0.8’den yüksek korelasyon da göstermemeli. bizim örneğimizdeki ölçeğin soruları genelde orta seviyede pozitif korelasyon gösteriyor, güzel. Aralarda birkaç tane 0’a çok yakın ya da negatif korelasyon var, bunlardan az sayıda varsa sorun değil. Ama 1 tanecik bile 0.8’den yüksek korelasyon görürsek bu bir sorun olur. O zaman 0.8’den büyük korelasyon gösteren soruların bir tanesini silip temel bileşen analizini yeniden başlatmak gerekir çünkü birbiriyle çok fazla ilişkili iki sorunun varlığı (multicollinearity) temel bileşen analizinin dengesini bozar.

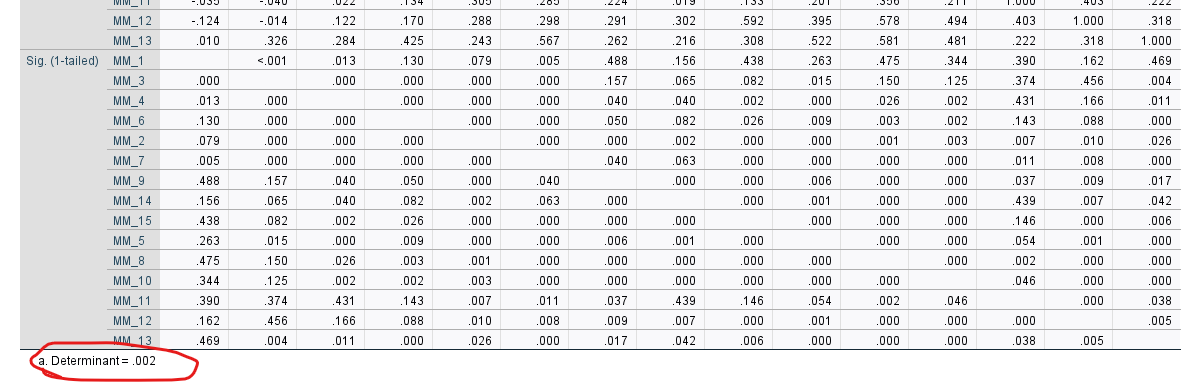
Yine “Correlation Matrix” tablosunun en altında Determinant değeri görünmektedir. Tabloyu bu sayfada gösterirken ikiye bölmek zorunda kaldım çünkü tek parça olarak ekrana sığmıyordu. Determinant değeri 0.00001’den büyük ise güzel. Eğer küçük ise bu demek oluyor ki sorular arasında yeterli ilişki bulunmamaktadır. O zaman temel bileşen analizi yapmamız pek anlamlı olmuyor olacak.

KMO and Bartlett’s Test tablosunda bakmamız gereken 2 değer var.

Kaiser-Meyer-Olkin => Bu değer 0.6’dan büyük olursa daha iyi.

Bartlett’s Test of Sphericity Sig. => Bu testin p değeri 0.05’ten küçük olursa daha iyi.

Genelde bu iki değer de istenen aralıklarda çıkar, bunlarla ilgili bir sorun çıkarsa örneklem temel bileşen analizine uygunsuz demektir (mesela örneklemimizde çok az sayıda katılımcı bulunuyor olabilir).

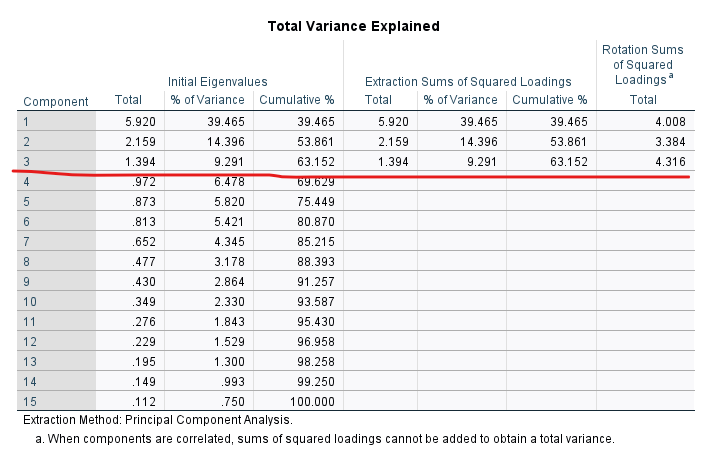
“Total Variance Explained” tablosunda SPSS’in soruları gruplandırma işlemi sırasında kaç adet temel bileşen belirlediğini görüyoruz. Analiz seçeneklerini seçerken Eigenvalue’ları 1’in üzerinde olduğu sürece temel bileşen olarak belirlesin demiştik. Bu doğrultuda SPSS soruları 3 temel bileşene ayırdı. Temel bileşen analizini yaptığımız soruların optimal gruplandırma şekli, 3 temel bileşene ayırmakmış demek ki. “Cumulative” sütununa bakarsak, bu temel bileşenlerin toplam varyansın %63’ünü açıkladığını görüyoruz. SPSS’in soruları atadığı temel bileşenlerin toplam varyansın en az %50’sini açıklıyor olması idealdir.

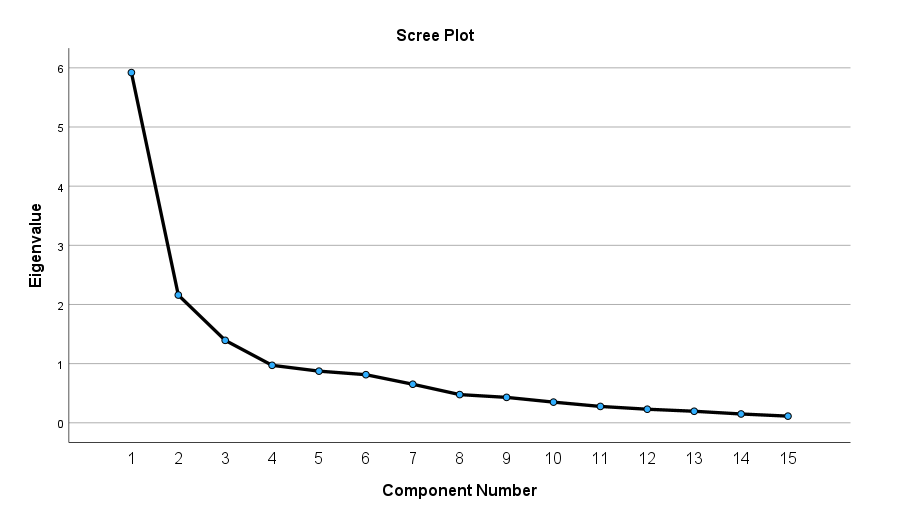
“Scree Plot” grafiğinde, temel bileşen sayısı arttıkça Eigenvalue’nun ne hızda düştüğünü görebiliyoruz. 1 temel bileşenli modelden 2 temel bileşenli modele geçince Eigenvalue çok hızlı düşmüş. Aynı şekilde 2 temel bileşenli modelden 3 temel bileşenli modele geçince Eigenvalue hızlı düşmüş. 3 temel bileşenli modelden 4 temel bileşenli modele geçerken ve sonrasında çok hızlı düşmemiş. Buradan da SPSS’in analize sokulan soruları sadece 3 temel bileşene ayırmış olmasının isabetli bir uygulama olduğunu doğrulamış oluyoruz.

Gelelim asıl önemli olan “Pattern Matrix” tablosuna. Orthogonal bir rotation yapmış olduğumuz için bakmamız gereken Matrix tablosu Rotated Component Matrix’tir, diğer Matrix tablolarına bakmamalıyız.

Rotated Component Matrix tablosunda, Temel Bileşen Analizi sonucunda, hangi soruların hangi temel bileşene atandığını (yüklendiğini) görebiliyoruz. Bu temel bileşen yüklemesi yorumlama aşaması, SPSS ile yapılan analizler arasında belirli kurallara bağlı siyah-beyaz doğru-yanlış yorumlama yapmanın en az mümkün olduğu durumlardan biri. Analizi yapan kişinin, analiz ettiği konuya hakim biri olması, bu aşamada daha iyi yorumlama yapabilmesini sağlayacaktır.

Analize başlarken hatırlarsanız SPSS’e 0.30’dan düşük temel bileşen yüklemelerini tabloda göstermemesini söylediğimiz için bu tabloda sadece 0.30’dan büyük değerler gözüküyor. Bu, hangi sorunun asıl olarak hangi temel bileşene/bileşenlere hangi temel bileşen yüküyle yüklendiğini daha kolay görmemizi sağlıyor. Tabloya bakınca bazı soruların sadece 1 temel bileşene yüklendiğini görüyoruz fakat 1’den fazla temel bileşene 0.30’dan büyük yükle yüklenen bazı sorular da var. Bu normaldir, özellikle Psikoloji gibi sosyal bilimlerde temel bileşen yükleri tablosu böyle biraz karmaşık çıkar, çok temiz çıkmaz.

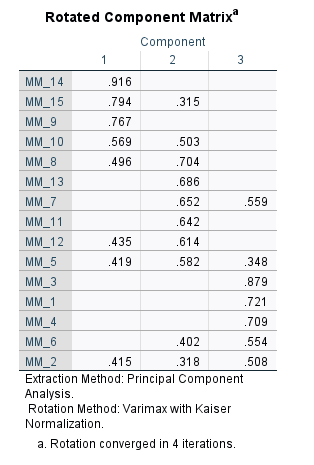
Yalnız demin dediğim gibi burada her soru tek 1 temel bileşene yüklenmemiş. Aynı anda 2 temel bileşene birbirine yakın güçlerde yüklenen sorular var. Mesela 14. ve 9. soruların sadece 1. temel bileşene güçlü şekilde yüklendiğini görmemize rağmen, 10. sorunun hem 1. hem 2. temel bileşene birbirine yakın güçlerde yüklendiğini, 7. sorunun da hem 2. hem 3. temel bileşene birbirine yakın güçlerde yüklendiğini görüyoruz. O zaman hangi sorunun hangi temel bileşene ait olması gerektiğine nasıl karar vereceğiz?

İşte burada devreye analiz yapan kişinin analiz yaptığı konuya hakimiyeti giriyor. Konuya ne kadar hakimse vereceği karar o kadar isabetli olacaktır. 1’den fazla temel bileşene güçlü yüklenen sorular için değişik yaklaşımlar benimsenebilir.

• Mesela bir yaklaşım olarak, eğer bir soru 2 temel bileşene güçlü şekilde yüklendiyse ve temel bileşenler arasında 0.100’den büyük bir fark varsa, sadece daha güçlü şekilde yüklendiği temel bileşene yüklenmiş gibi davranabiliriz.
• Diğer bir yaklaşım olarak eğer bir soru iki temel bileşene güçlü şekilde yüklendiyse, bu soruyu tamamen analizden çıkartıp yeniden bir temel bileşen analizi yapabiliriz. Bir ölçekten bu şekilde çok fazla sorunun çıkartılması önerilmez.
• Üçüncü bir yaklaşım olarak, bir soru iki temel bileşene güçlü şekilde yüklendiyse, sorulara gidilerek sorular okunur. Alan hakimiyeti devreye girer dediğim asıl nokta burasıydı. Mesela 10. soru hem 1. hem 2. temel bileşene birbirine çok yakın değerlerde güçlü şekilde yüklenmiş. Yalnızca 1. temel bileşene güçlü olarak yüklenen 14. ve 9. soruları okuyalım, sonra yalnızca 2. temel bileşene güçlü olarak yüklenen 11. ve 13. soruları okuyalım, en son da 7. soruyu okuyalım. 7. soruyu hangi temel bileşene tek başına yüklenen sorulara yakın görüyorsak, onu sadece o temel bileşene yüklenmiş gibi sayabiliriz. Bu kararı verirken yargı gücümüzü kullanmalı ve elle tutulur sebepler göstererek kararımızı destekleyebilmeliyiz.
• Yine farklı bir yaklaşım olarak şunu yapabiliriz: Mesela bu örnekteki tabloya baktığımızda, hem 1. temel bileşene hem 2. temel bileşene birlikte yüklenen birçok soru olduğunu görüyoruz. Yukarıdan hatırlarsak, Sorumluluk ölçeğinin alt ölçeklerinden olan 1. temel bileşenin Görev Bilinci, 3. temel bileşenin ise İnisiyatif Almak olduğunu biliyoruz. Bu iki temel bileşene birlikte yüklenen çok soru olmasından dolayı, şöyle bir öneri ortaya atabiliriz: “Belki de Görev Bilinci ve İnisiyatif Almak konuları, aynı şeyi temsil ediyordur.” O zaman bu ikisini tek 1 temel bileşen olarak sayabiliriz. Eğer böyle bir karar veriyorsak bunu somut gerekçeler göstererek desteklememiz gerekir (mesela literatürden bu yönde makaleler bulup referans vermek). Bunu yaptıktan sonra aynı veriyle bir Açımlayıcı Faktör Analizi yaparsak (Direct Oblimin rotasyonu ile) ve Extract adımında SPSS’e soruların 2 faktöre ayrılacağını söylersek yeni faktör analizi sonucu gelen Pattern Matrix tablosu daha temiz görünecektir.

Dediğim gibi, temel bileşen analizi tabloları çok farklı yorumlamalara açıktır ve hangi kararın isabetli hangisinin isabetsiz olduğunu belirlemek net değildir. Kişinin temel bileşen analizi yaptığı konuda uzman birisi olması, temel bileşen analizi sonucunda daha isabetli kararlar vermesine çok yardımcı olmaktadır.

Temel bileşen analizi konusu bu kadardı. Biraz karmaşık bir karar verme süreci var fakat iyi bir istatistikçiyi amatör bir istatistikçiden ayıran en önemli konulardan biri de böyle belirsizlikler karşısında verdikleri kararları nasıl verdiğidir. Buraya kadar okuduğunuz için tebrikler & teşekkürler, tekrar görüşmek üzere.