Bland-Altman Analizi (SPSS) — Resimli

Ölçüm tekniklerinin karşılaştırılması ve uygunluğunun değerlendirilmesi için Bland-Altman analizi oldukça etkili bir araçtır. Bu analiz, ölçümlerin iki farklı yöntem veya araçla alındığında ortaya çıkan farkların ve tutarsızlıkların detaylı bir şekilde incelenmesini sağlar. Bu blog yazısında, SPSS kullanarak Bland-Altman grafiği oluşturma ve yorumlama sürecini adım adım ele alacağız.

Bland-Altman Grafiği Nedir? Bland-Altman Analizi Ne İşe Yarar?

Bland-Altman analizi, iki ölçüm yöntemiyle aynı şeyin ölçümü, iki farklı test zamanında aynı şeyin ölçümü ya da iki farklı gözlemcinin aynı şeyi ölçümü arasındaki tutarlılığı değerlendirmek için kullanılan istatistiksel bir yöntemdir. Bland-Altman yöntemi, ölçümler arasındaki farkları ve bu farkların ortalamasına karşı farkları göstermek için özel bir grafik olan Bland-Altman grafiği (Bland-Altman plot) kullanır.

Bland-Altman grafiği, ölçümler arasındaki farklarla bunların ortalamalarını karşılaştıran ve sonucu görsel olarak gösteren bir grafiktir. Bu grafik, iki ölçüm yöntemi arasındaki tutarsızlıkları veya farklılıkları hızlıca değerlendirmek için yaygın olarak kullanılır. Eğrinin yatay ekseni, iki yöntem arasındaki farkı (Y1 – Y2) temsil ederken, dikey ekseni ise bu farkların ortalamasını [(Y1 + Y2) / 2] gösterir. Her veri noktası, ölçümler arasındaki farkı ve bu farkın ortalamasını belirtir.

Bland-Altman analizi şu adımlarla gerçekleştirilir:

1. Veri Toplama: İki farklı yöntem veya testle aynı nesne veya özelliği ölçen veriler toplanır. Örneğin, bir sağlık testi için iki farklı cihazla yapılan ölçümler.
2. Farkların ve Ortalamanın Hesaplanması: İki ölçüm yöntemi arasındaki fark (Y1 – Y2) ve bu farkların ortalaması [(Y1 + Y2) / 2] hesaplanır. Her bir ölçüm için bu farklar ve ortalamalar kaydedilir.
3. Bland-Altman Grafiğinin Oluşturulması: Her bir ölçüm için hesaplanan farklar ve ortalamalar kullanılarak Bland-Altman plotu oluşturulur. Bu grafik, ölçüm farklarının ortalamalarına göre nasıl dağıldığını gösterir.
4. Analiz ve Yorum: Bland-Altman grafiği incelenir ve ölçümler arasındaki tutarsızlıklar veya farklılıklar görsel olarak değerlendirilir. Özellikle, farkların ortalamasına göre değişimlerin dağılımı incelenir. Bu analizde, ölçümler arasındaki klinik önemi olan tutarsızlıklar veya sapmalar belirlenir.

Bland-Altman analizi sonuçlarından neler öğrenebiliriz?

• Limitler: Analiz, farkların ortalama üzerindeki dağılımını belirleyerek güven aralıklarını da sağlar. Bu limitler, ölçüm farklarının kabul edilebilir sınırlar içinde mi yoksa önemli sapmalar içerip içermediğini belirlememize yardımcı olur.
• Biyolojik ve Klinik Anlamlılık: Elde edilen sonuçlar, ölçüm farklarının biyolojik veya klinik anlamını değerlendirir. Yani, bu farkların hastaların tedavi veya teşhis süreçlerini nasıl etkileyebileceğini anlamamıza yardımcı olur.

SPSS ile Bland-Altman Analizi Nasıl Yapılır?

Bu örnekte, aynı kişilerin Duygusallık skoru iki farklı ölçüm aracıyla ölçülüyor. Bu ölçümlerin birbiriyle uyumunu test etmek için Bland-Altman Analizi yapacağız. Gördüğünüz gibi iki ölçüm aracının bulduğu sonuçlar birbirlerine çok yakın ama biz istatistiksel olarak gerçekten birbiriyle ilişkisi nasıl bunu görmek için analiz yapmalıyız.

Önce, fark ve ortalama skor değişkenleri oluşturmamız gerekiyor.

Transform -> Compute Variable

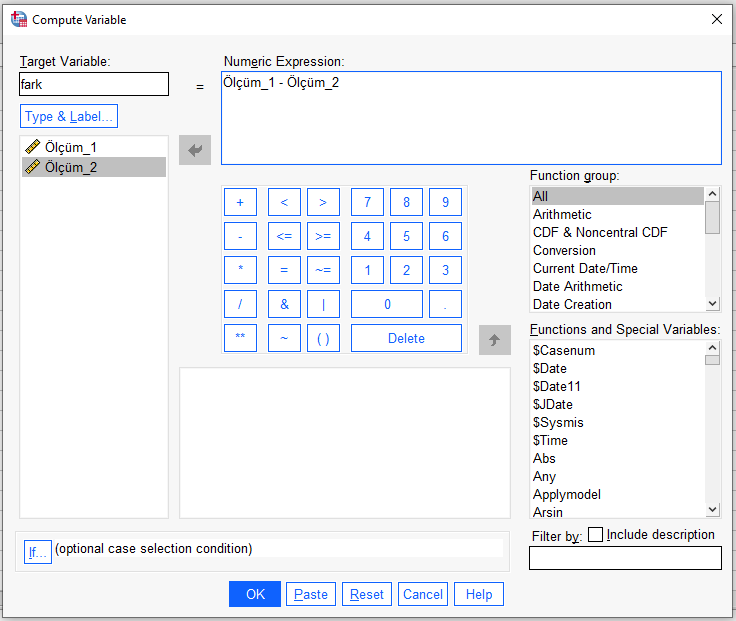
Fark değişkeni oluşturmak için iki değişkeni birbirinden çıkartmamız gerekiyor.

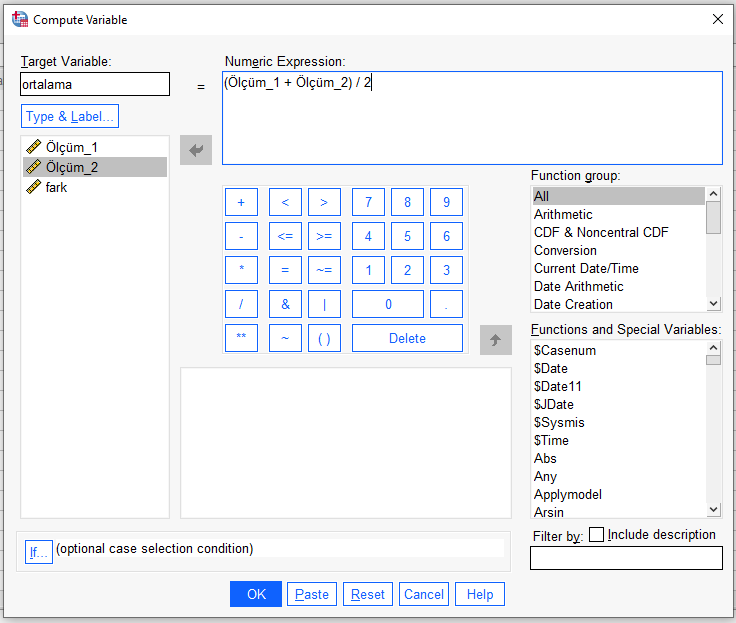
Aynı şekilde ortalama değişkeni için de ikisini toplayıp sonucu 2’ye bölmek gerekiyor.

SPSS veri setinizde göreceğiniz gibi Fark ve Ortalama isimli iki yeni değişken oluşmuş olacak.

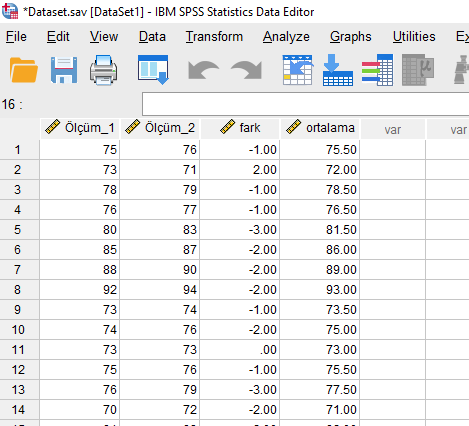
Şimdi, önce Fark değişkeninin 0’dan istatistiksel olarak anlamlı biçimde farklı olup olmadığına bakmamız gerekiyor. Eğer 0’dan anlamlı biçimde fark varsa, bu demek olur ki iki ölçüm aracı birbirine eşit ölçmemişlerdir. Bir ölçüm aracı diğerinden anlamlı biçimde daha yüksek (veya düşük) ölçmüştür demek olacaktır. Bunu test etmek için Tek Örneklem T Testi yapacağız.

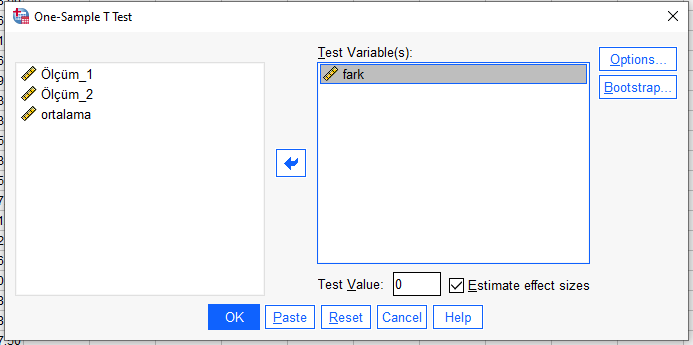
Analyze -> Compare Means -> One-Sample T Test

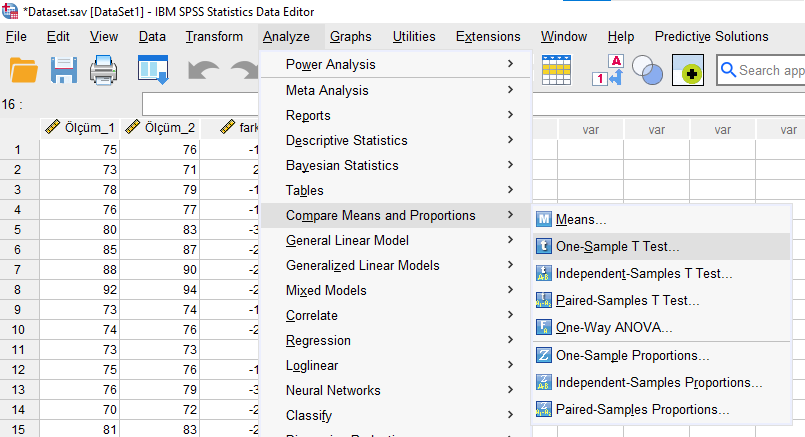
Fark değişkenini Test Variable kutusuna atıyoruz. Altındaki Test Value kutusuna “0” yazıyoruz. Sonra “OK”a basıyoruz.

“One-Sample Statistics” tablosunda, Fark değişkeninin ortalamasını, yani iki ölçüm aracının yaptığı ölçümlerin farkının ortalama miktarını görüyoruz. Bu örnekte bir ölçüm aracı diğerinden ortalama 0.8224 daha yüksek ölçmüştür. Bu farkın istatistiksel olarak anlamlı olup olmadığına da “One-Sample Test” tablosundan bakacağız.

“One-Sample Test” tablosundaki “Two-Sided p” değeri 0.05’in üzerinde (p = 0.380). Yani, iki ölçüm aracı arasındaki 0.8224’lük fark, istatistiksel olarak anlamlı bir fark değildir. Yani, “iki ölçüm aracı birbirlerinden istatistiksel olarak farklı ölçmüyor” sonucuna varabiliriz.

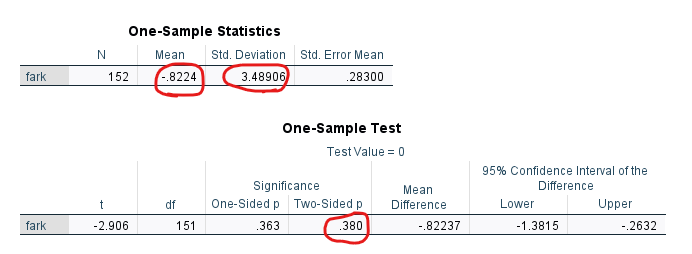
Şimdi, çizeceğimiz Bland-Altman grafiğinin %95 güven aralıklarını hesaplamamız gerekiyor. Bunu SPSS fonksiyonuyla yapamıyoruz, elimizle hesaplamamız gerekiyor.

Yukarıdaki T Testi’nde “One-Sample Statistics” tablosunda bulduğumuz ortalama ve standart sapma skorlarını (yuvarlak içine aldığım) bir yere not alalım. Excel’e not aldım ben kolay diye.

Sonra şu formülü uyguluyoruz:

%95 Güven aralığı üst sınırı = Ortalama Değer + (1.96 x Standart Sapma)

%95 Güven aralığı alt sınırı = Ortalama Değer – (1.96 x Standart Sapma)

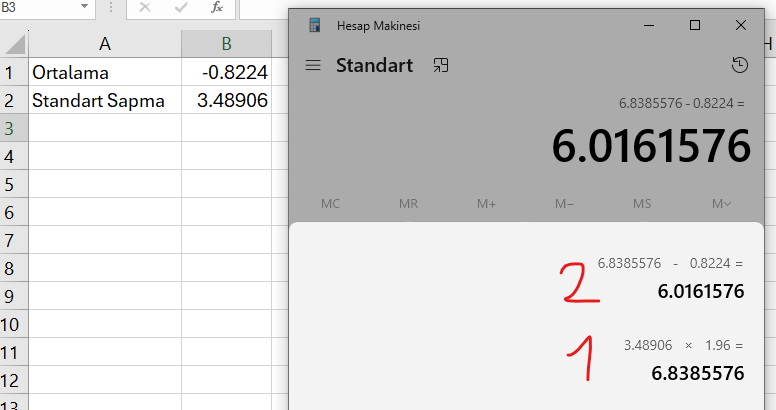
İşlemlerimiz sonucu aşağıdaki güven aralığı alt ve üst sınırlarını bulduk.

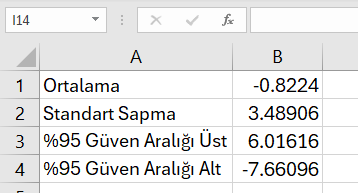
Şimdi, SPSS ile Bland-Altman Grafiği oluşturmaya başlayalım.

Graphs -> Scatter/Dot

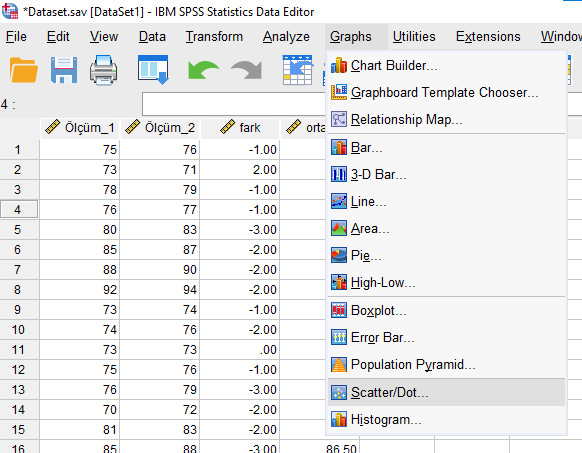
Açılacak pencerede “Simple Scatter” seçtikten sonra karşımıza bu pencere gelecek. Bu pencerede Y Axis’e Fark, X Axis’e de Ortalama değişkenlerini yerleştiriyoruz. Sonra “OK”a basıyoruz.

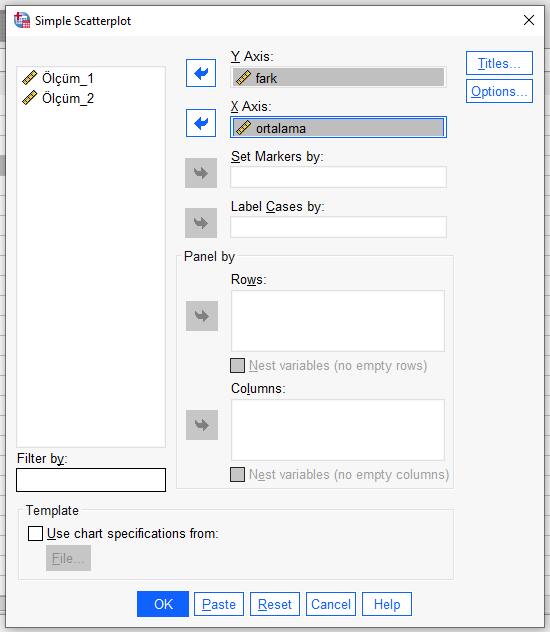
SPSS karşımıza aşağıdaki gibi bir Fark-Ortalama nokta grafiği çıkartıyor.

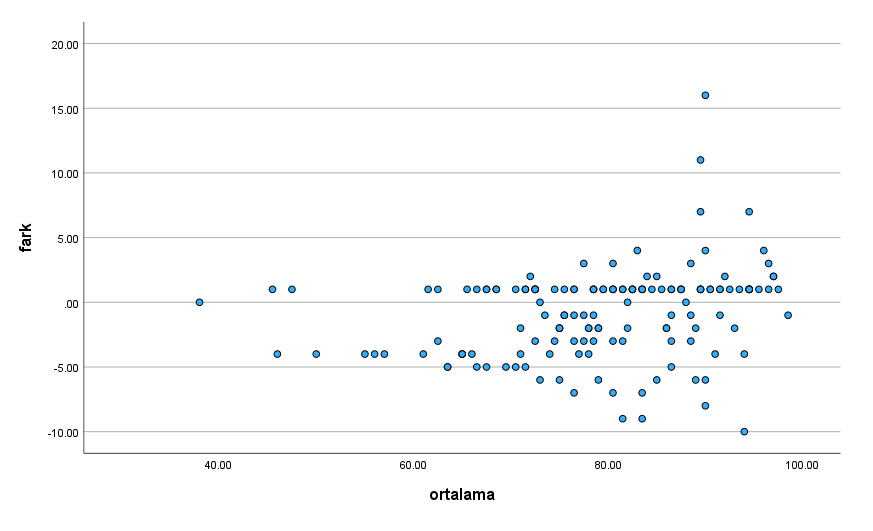
Bu grafiğe mouse ile çift tıklarsak grafik editörü penceresi açılacak. Açıldıktan sonra üstteki menüden “Add a reference line to the Y axis” seçeneğine basıyoruz.

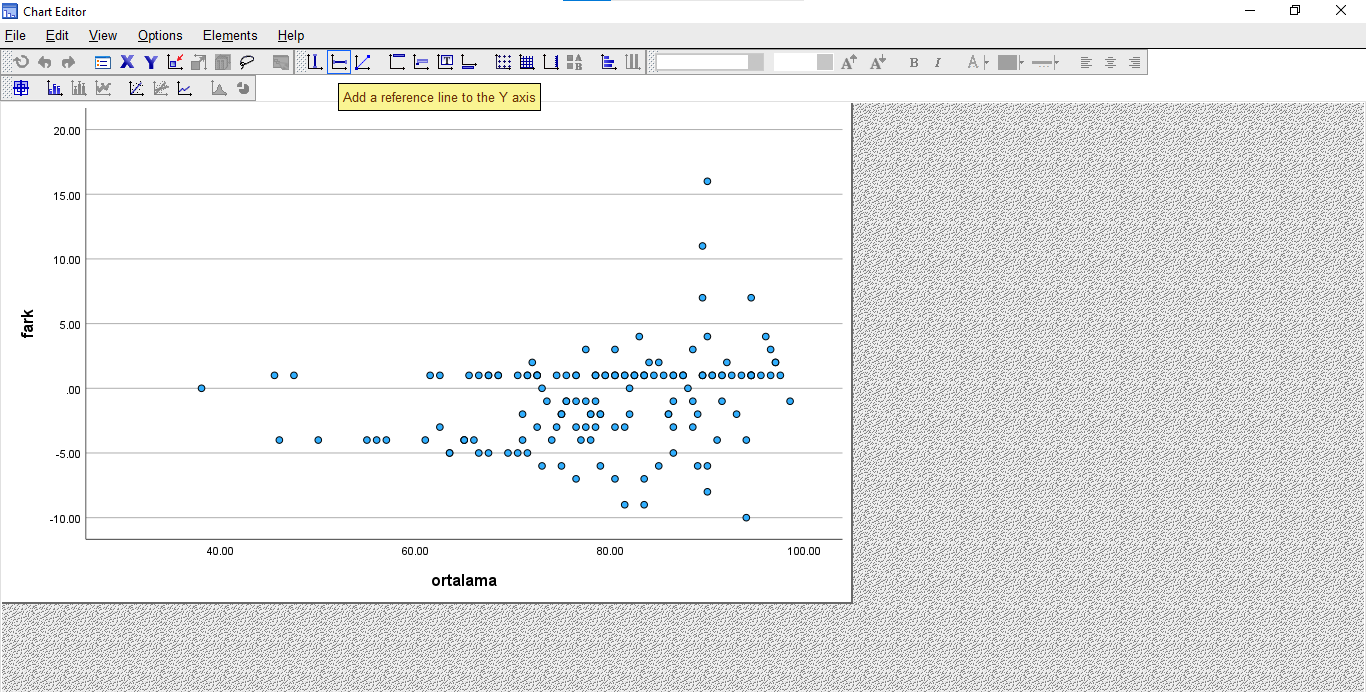
Bastıktan sonra SPSS grafiğe yatay bir çizgi ekleyecek. Bu çizgiyi, iki ölçümün farkının ortalama değeri olan -0.8224 seviyesinden çizmek istiyorum. Bu yüzden Properties penceresinde Position kutusuna bu değeri yazıyorum.

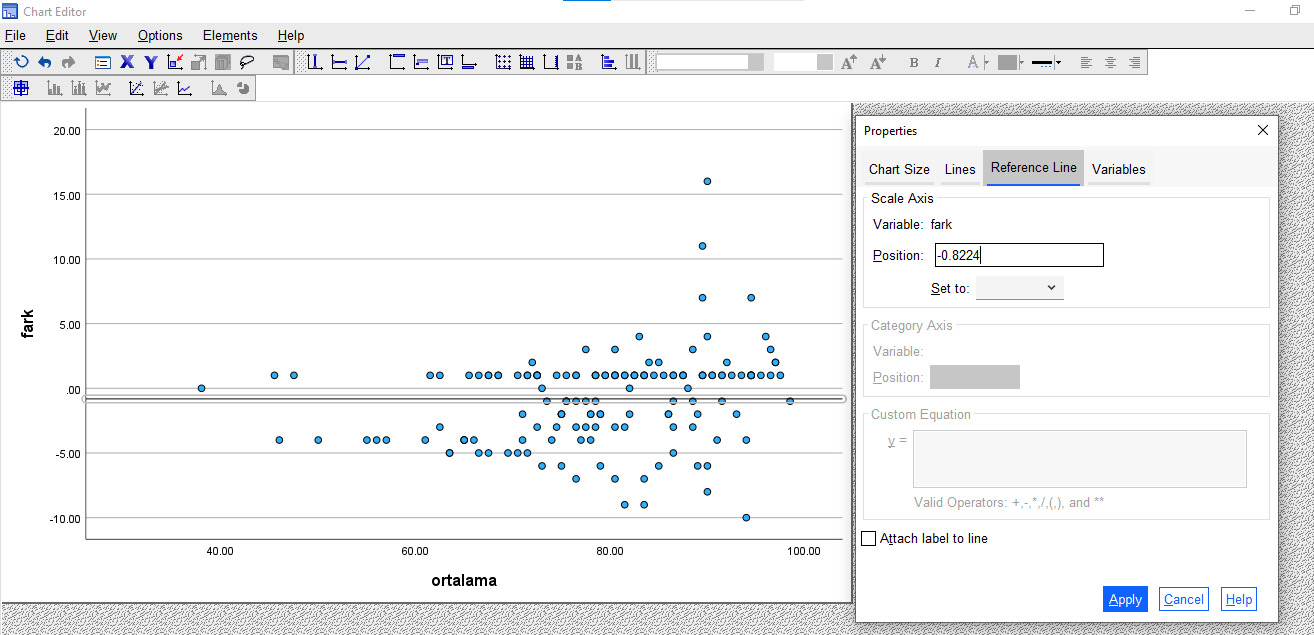
Aynı şekilde, aynı butonlara basarak üst ve alt sınırı olarak 6.01616 ve -7.66096 değerleri için de yatay birer çizgi çekiyorum. Grafik sonunda aşağıdaki gibi görünüyor.

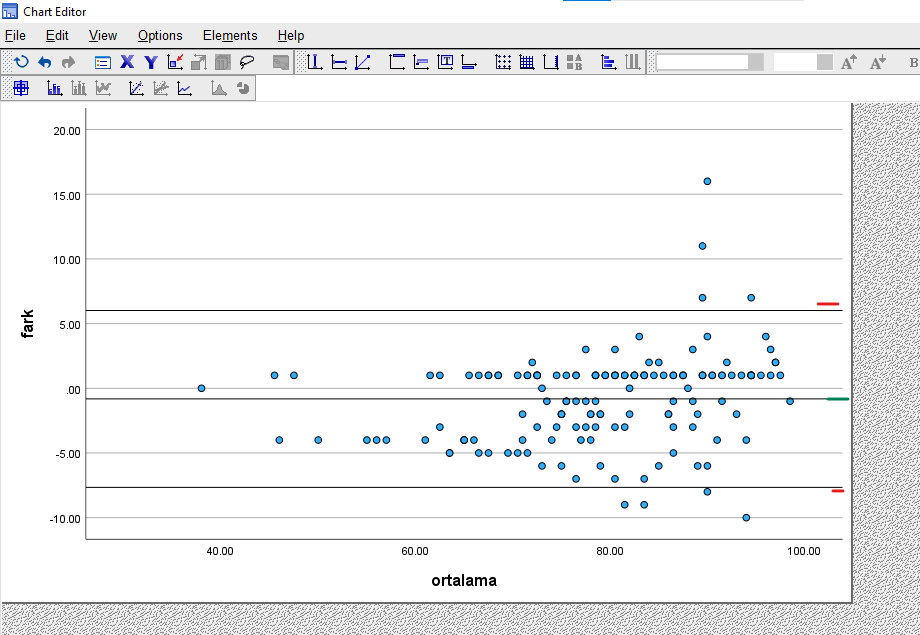
Bland-Altman grafiğimiz yukarıdaki gibidir. Bunun altında ve üstünde çok fazla nokta olmamasını istiyoruz. Aynı zamanda, orta çizginin üstünde ve altında kalan noktaların oranının yatay eksendeki Ortalama değeri arttıkça değişmemesini istiyoruz. Aksi takdirde iki ölçüm aracının ölçümleri Bias yani yanlılık‘a sahip demek olacaktır.

Son adım olarak iki ölçüm aracının ölçümleri Bias’e sahip mi diye bakalım.

Analyze -> Regression -> Linear

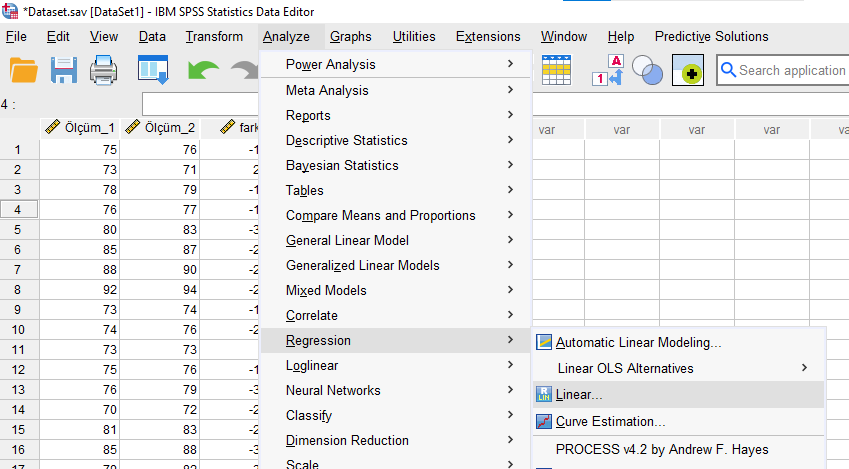
Fark’ı Dependent, Ortalama’yı da Independent kutusuna yerleştirelim ve “OK”a basalım.

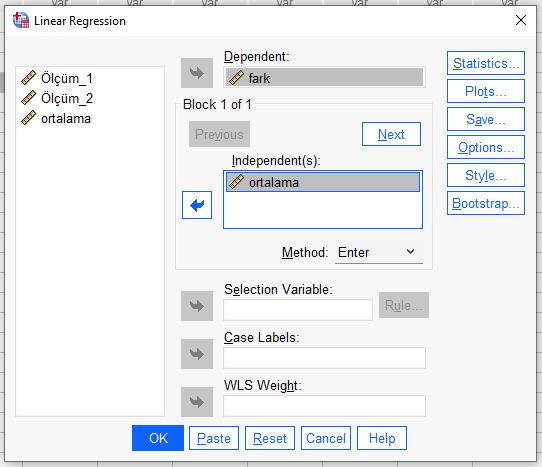
Regresyon analizi sonucunda “Coefficients” tablosundaki Ortalama satırındaki B değerini 0’a olabildiğince yakın istiyoruz ve aynı zamanda bu satırdaki p değerini de non-significant istiyoruz. Bu ikisi de varsa “demek ki iki ölçüm aracı, herhangi bir yanlılığa düşmeden ölçüm yapmışlardır” demek oluyor.

0.05’ten küçük istatistiksel olarak anlamlı bir sonuç, örneğimizde orantısal yanlılık olduğu anlamına gelir. Yani bu örnekte sonuç pozitif olduğu için Ortalama değer büyüdükçe iki ölçüm aracının ölçümleri arasındaki Fark da biraz artmaktadır.

Bu örnekte Sig. p anlamlılık değerinin 0.001’den küçük olması ve B değerinin 0.077 olması şu anlama gelmektedir: “İki ölçümün Ortalama’sının değeri 1 birim artınca, iki ölçümün Fark’ı da 0.077 birim artmaktadır.” Bu normalde istemediğimiz bir durumdur çünkü bir yanlılıktır ve yanlı ölçüm istatistiksel açıdan yanıltıcı sonuçlar verebilir, fakat B değeri 0’a oldukça yakın, 0.077 değerinde. B değeri 0’a çok yakın olduğu için bu örnekte bir sorun yok diyebiliriz fakat normalde Sig. sütunundaki p değerinin de 0.05’ten büyük olmasını tercih ederdik.

SPSS ile Bland-Altman Analizi bu kadardı. İki ölçüm aracının ölçümlerini karşılaştırmak için Fark ve Ortalama değişkenleri oluşturduk, Bland-Altman Grafiği (Bland-Altman Plot) oluşturduk ve son olarak ölçümlerde yanlılık (bias) var mı diye baktık.