SPSS ile ANCOVA Analizi (Resimli)

ANCOVA analizi, birçok araştırmada kullanılan ve değişkenleri kontrol etmek amacıyla kullanılan bir istatistiksel analiz yöntemidir. Bu yöntem, bağımsız değişkenlerin etkisini kontrol etmek ve düz ANOVA’ya göre gruplar arasındaki farkları daha doğru bir şekilde değerlendirmek için kullanılır. Bu blog yazısında, ANCOVA analizinin ne olduğunu, varsayımlarını, SPSS ile nasıl yapılacağını ve analiz sonuçlarının nasıl yorumlanacağını öğreneceksiniz.

ANCOVA Analizi Nedir?

ANCOVA Analizi, normal bir ANOVA analizi sonucuna bir veya daha fazla kovaryantın etkilerini kontrol ederek grup ortalamalarını karşılaştırmak için kullanılan istatistiksel bir tekniktir. Kovaryantlar, asıl araştırılan değişken olmayan ancak bağımlı değişken üzerinde etkisi olduğuna inanılan bağımsız değişkenlerdir. ANCOVA, bu kovaryantları model içine dahil ederek ANOVA’nın prensiplerini genişletir ve araştırmacıların bağımlı değişken üzerinde etkisi olan bağımsız değişkenlerin etkilerini istenmeyen diğer bağımsız değişkenlerden daha iyi izole etmelerini sağlar.

ANCOVA’da temel amaç, kovaryantların etkilerini hesaba katarak grup ortalamaları arasında önemli farklılıklar olup olmadığını belirlemektir. Bu, bağımlı değişken ortalamalarını kovaryantların etkileri için ayarlayarak hata varyansını azaltır ve analizin istatistiksel gücünü ANOVA’ya kıyasla artırabilir.

ANCOVA modeli, kovaryantların etkileri hesaba katıldıktan sonra asıl araştırma konusu olan bağımsız değişken için katsayının sıfırdan önemli ölçüde farklı olup olmadığını test eder.

ANCOVA Örneklemi Nasıl Olmalı?

Temel bir ANCOVA örneklemi, 1 bağımlı değişken, 1 bağımsız değişken, 1 de kovaryant olan 3 farklı değişkenden oluşur. Eğer 2 tane bağımsız değişken olursa o zaman İki Yönlü ANCOVA olmuş olur. Eğer 2 veya daha fazla bağımlı değişken olursa MANCOVA olmuş olur.

ANCOVA Analizi Varsayımları

ANCOVA analizi, istatistiksel çıkarımın geçerliliğini sağlamak için bir dizi varsayıma dayanır. Bu varsayımlar, ANCOVA’nın sonuçlarını yorumlamadan önce değerlendirilip karşılanmalıdır. Eğer karşılanıyorsa ANCOVA analizimizin sonuçlarına güvenebileceğiz demektir. Varsayımlar şunlardır:

1. Kovaryantların Gruplar Arası Eşitliği: Kovaryant, farklı gruplar arasında farklı değere sahip olmamalıdır. Kovaryantın değeri her grup için yaklaşık eşit olmalıdır.
2. Regresyon Eğrilerinin Homojenliği: Bağımlı değişken ve kovaryant, bağımsız değişkenin her grubu içinde aynı korelasyona sahip olmalıdır.
3. Normal dağılım: Normal ANOVA’daki normallik varsayımı şartları sağlanmalıdır.
4. Uç Değer Olmaması: Normal ANOVA gibi, ANCOVA analizi de örneklem büyüklüğü yeterince büyükse veride uç değerler bulunmasına karşı dayanıklıdır. Yine de, analiz edilecek veride mümkün olduğunca uç değer bulunmamalıdır.

SPSS ile ANCOVA Analizi Varsayımları Test Etme

Normal dağılım ve uç değer bulunmama varsayımları, bütün ANOVA analizlerinde geçerli olduğu için, ANCOVA başlığı altında ayrıca anlatmayacağım sayfanın gereksiz uzamaması için. Bunları ANOVA analizi ve uç değer bulma yazılarımı okuyarak halledebilirsiniz. Bu sayfada sadece ANCOVA’ya özel varsayımların SPSS ile nasıl test edildiğini anlatacağım.

SPSS ile ANCOVA analizi öncesinde varsayımları aşağıdaki gibi test edebiliriz. Bu örnekte, 3 cinsiyet grubu (erkek, kadın, diğer) arasındaki depresyon miktarlarının farkının “sosyal destek” değişkeninin kovaryant olarak hesaba katıldığı durumda hâlâ geçerli olup olmadığını test etmek için ANCOVA analizi yapacağız.

Kovaryant’ın Bağımsız Değişken Grupları Arasında Farklı Olmama Varsayımı

Analyze -> General Linear Model -> Univariate

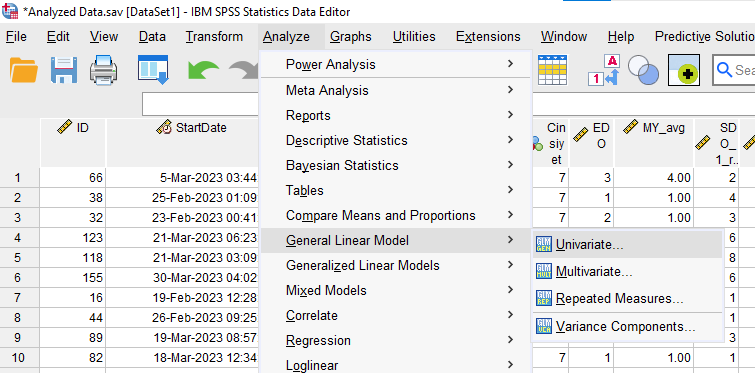
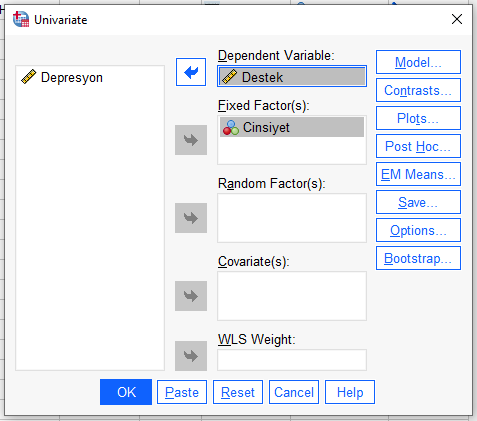
Bağımsız değişkenimizi Fixed Factors kutusuna koyuyoruz. Kovaryant olan değişkeni ise Dependent Variable kutusuna koyuyoruz. Unutmayın, şu an ANCOVA yapmıyoruz, sadece varsayım test ediyoruz.

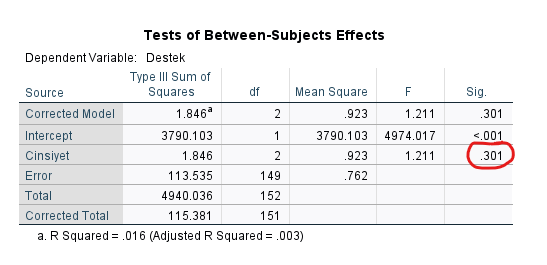
OK’a bastıktan sonra SPSS’in verdiği tablolardan “Tests of Between-Subjects Effects” tablosuna bakmak gerekiyor. Burada, Sig. p değerinin 0.05’ten büyük olmasını istiyoruz. Eğer öyleyse kovaryant, bağımsız değişkenin farklı gruplar arasında farklı değere sahip değil demektir ve bu ANCOVA analizine devam etmemiz için iyi bir işarettir.

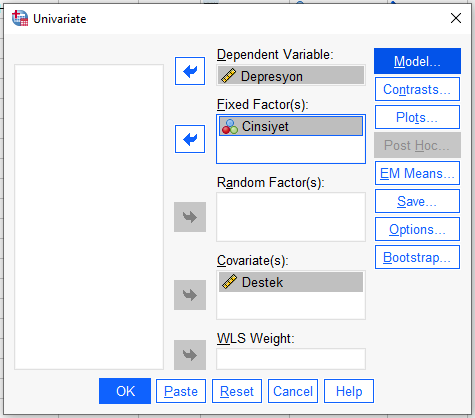
Regresyon Eğrilerinin Homojenliği Varsayımı

Analyze -> General Linear Model -> Univariate

Bağımlı değişkenimizi Dependent Variable, bağımsız değişkenimizi Fixed Factors, kovaryantımızı da Covariate kutusuna atıyoruz. Sonra “Model” butonuna basıyoruz.

Açılacak yeni pencerede Specify Model bölümünde Build Custom Terms seçiyoruz. Sonra soldaki kutudan sırayla önce sadece bir değişkeni, sonra sadece diğer değişkeni, sonra ikisini birlikte seçip sağdaki Model kutusuna atıyoruz. Continue’ya basabiliriz.

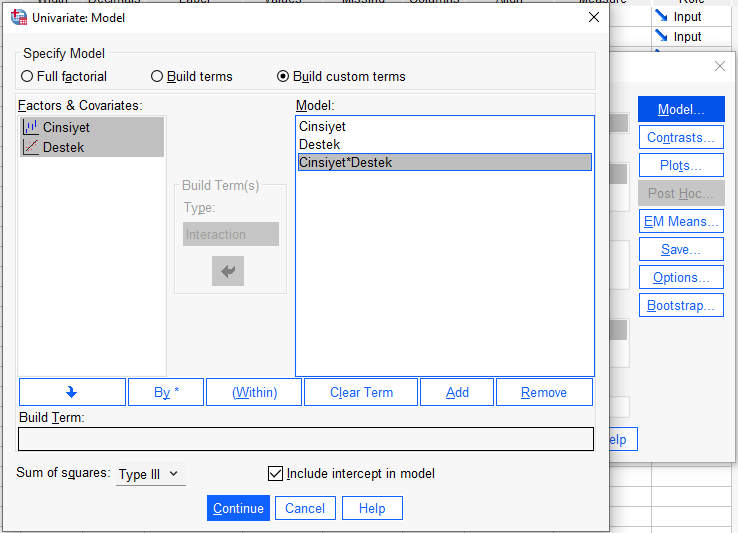
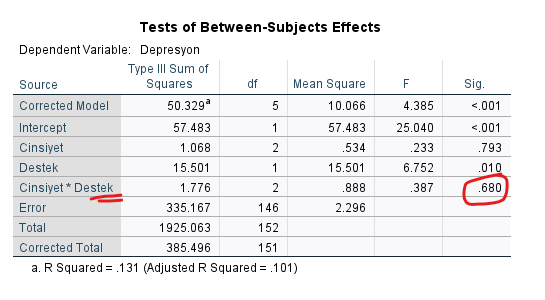
OK’a basınca, SPSS bize aşağıdaki tabloyu sunacak. Burada tek bakmamız gereken yer 2 değişkenin etkileşiminin olduğu satır. Bu satırdaki Sig. p değerinin 0.05’in üzerinde olmasını istiyoruz. Eğer böyleyse regresyon eğrilerinin homojenliği varsayımı doğrulanmış demek oluyor. Güzel, ANCOVA analizimizi yapmaya başlayabiliriz artık.

SPSS ile ANCOVA Analizi Nasıl Yapılır?

Bütün varsayımları doğruladığımıza göre artık ANCOVA analizimize geçebiliriz.

Bu örnekte, düz bir ANOVA yaptığımızda 3 Cinsiyet grubunun (erkek, kadın, diğer) Depresyon miktarları farklı bulunmuş. Bu 3 grubun arasındaki Depresyon miktarlarının farkının “sosyal destek” isimli başka bir değişkenin Kovaryant olarak hesaba katıldığı durumda da hâlâ geçerli olup olmadığını görmek için ANCOVA analizi yapacağız.

Analyze -> General Linear Model -> Univariate

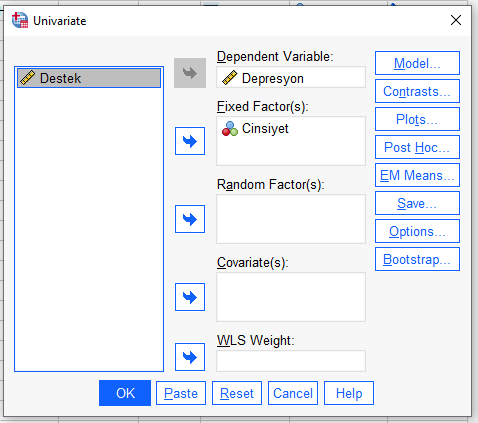
Açılan pencerede “Reset” butonuna basalım. Sonra, en baştan bağımlı değişkenimizi Dependent Variable, bağımsız değişkenimizi Fixed Factors, kovaryantımızı da Covariate kutusuna atıyoruz.

Options’a basıp aşağıdaki üç seçeneği işaretliyoruz.

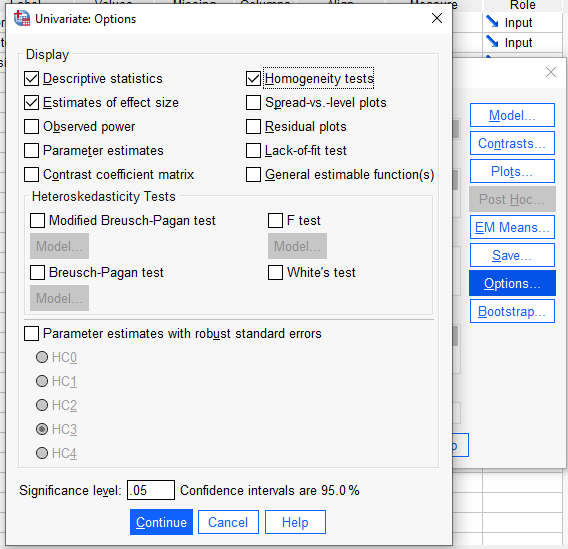
Fark ettiniz mi bilmiyorum ama Univariate ANCOVA penceresinde Covariate kutusuna kovaryantı koyduğunuz zaman penceredeki “Post Hoc” butonu silik görünmeye başladı. Bunun sebebi modelde kovaryant olduğu zaman Post Hoc test uygulanamamasıdır. Bağımsız değişkenimiz 2’den fazla gruba sahipse, eğer istatistiksel olarak anlamlı bir ANCOVA testi çıkması durumunda hangi grupların anlamlı olarak birbirinden farklı olduğunu “EM Means” butonu ile bulabiliyoruz.

EM Means açılır penceresinde bağımsız değişkenimizi sağdaki Display Means kutusuna koyup Compare Main Effects’e basıp Confidence Interval Adjustment’ı da Bonferroni olarak seçmeliyiz.

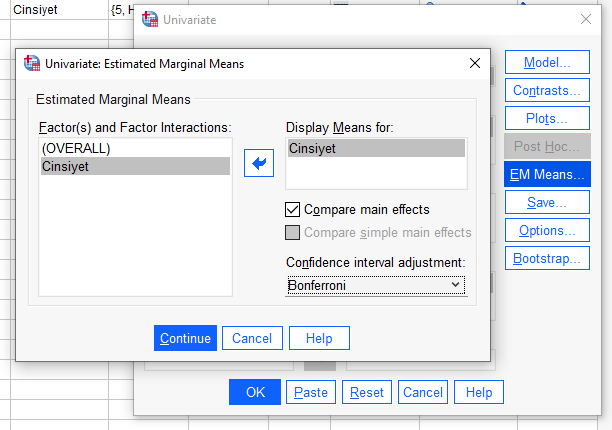
Sonra Continue ve OK’a basarak analizimizi başlatabiliriz.

(Reset yapınca Model kısmında Full Factorial seçili olmaya başladı. Düzgün ANCOVA analizi yapılması için böyle seçili olmalıdır.)

ANCOVA Analizi SPSS Tablo Yorumlama

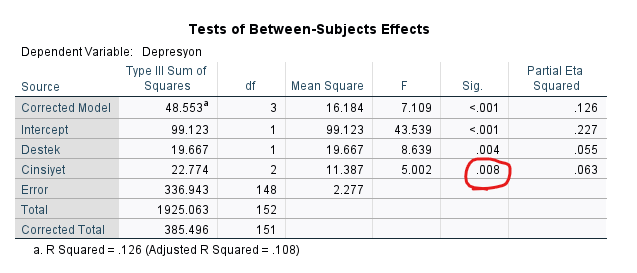
SPSS’in vereceği ANCOVA analizi tablolarında ilk bakmak gereken Cinsiyet satırındaki Sig. p değeridir. Bu değer 0.008 yani istatistiksel olarak anlamlı. O zaman ANCOVA analizinden şöyle bir sonuca varabiliriz: “Cinsiyetler arası Depresyon skorları, Sosyal Destek değişkeni hesaba katıldığı zaman bile farklılık göstermektedir.”

Bu arada Partial Eta Squared değerine de değinelim. Burada Partial Eta Squared’in 0.063 çıkması, bu ANCOVA analizinde orta büyüklükte bir etki görüldüğünü temsil eder.

ANCOVA vs. Düz ANOVA Tabloları Farkı

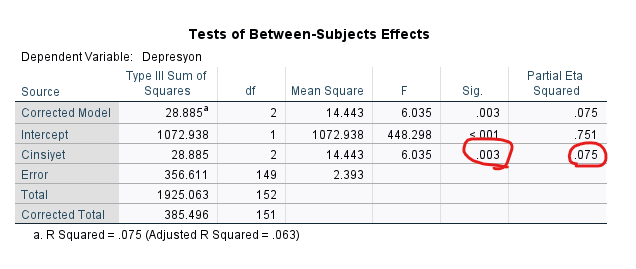
ANCOVA’nın düz ANOVA’dan farkını göstermek için, aynı analizi, kovaryant olmadan yapalım ve ANOVA tablosuna bakalım.

Gördüğünüz gibi, arada Sosyal Destek kovaryantının hesaba katılmadığı durumda, Cinsiyetler arası Depresyon skoru farkının anlamlılık p değeri 0.003 çıktı. Etki büyüklüğü ise 0.075 çıktı yani ANCOVA sonucundan biraz daha yüksek.

Bu durum da şöyle yorumlanabilir: “Sosyal Destek, az da olsa, Cinsiyetler arasındaki Depresyon skoruna etki ediyormuş. Ama Cinsiyetler arası Depresyon skorlarında anlamlı bir farklılık, arada Sosyal Destek kovaryantının kontrol edildiği durumda bile geçerlidir.”

ANCOVA Sonrası Hangi Gruplar Arası Farklılık Olduğunu Bulma

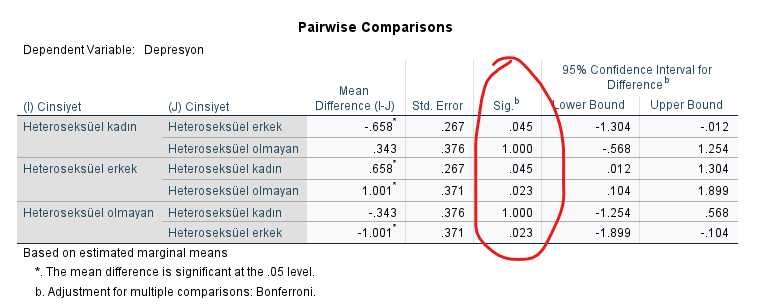
İstatistiksel olarak anlamlı bir ANCOVA sonucu bulduk, fakat hangi Cinsiyetler arasında Sosyal Destek kontrol edildiğinde dahi anlamlı olarak farklı Depresyon skorları görüldüğüne bakmak için SPSS’in ANCOVA analizimiz sonucu diğer tablolarla birlikte vermiş olduğu şu tablolara bakmamız gerekiyor:

“Pairwise Comparisons” başlıklı tabloda, bağımsız değişkenin her grup çiftinin arasındaki Depresyon skoru farkının istatistiksel olarak anlamlı olup olmadığını görebiliyoruz. Bu örneğe göre, Kadın ve Erkek arasında anlamlı bir Depresyon skoru farkı varmış (p=0.045). Erkeklerin ortalama Depresyon skoru Kadınlardan anlamlı bir şekilde 0.658 puan daha yüksekmiş. Erkeklerle Diğer cinsiyettekiler arasında da anlamlı bir ortalama Depresyon skoru farkı varmış (p=0.023). Erkeklerin ortalama Depresyon skoru Diğer cinsiyettekilerden anlamlı bir şekilde 1.001 puan daha yüksekmiş. Kadınlarla Diğer cinsiyetteki katılımcılar arasında ise anlamlı bir Depresyon skoru farkı yokmuş (p=1.000).

ANCOVA analizi ve düz ANOVA analizi ile karşılaştırması ve sonrasında gruplar arasındaki farkları inceleme işlemi bu kadardı. Eğer buraya kadar okuduysanız artık ANCOVA’nın düz ANOVA’dan neden daha faydalı bir analiz olduğunu anlamışsınızdır. Okuduğunuz için teşekkürler.