SPSS ile Çoklu Doğrusal Regresyon (Resimli)

Çoklu doğrusal regresyon analizi, istatistiksel bir yöntemdir ve bir bağımlı değişkenin bir veya daha fazla bağımsız değişkenle ilişkisini incelemek için kullanılır. Bu yöntem, birçok alanda kullanılmakta ve araştırmacıların verileri anlamalarına ve tahmin yapmalarına yardımcı olmaktadır. Ancak, çoklu doğrusal regresyon analizi kullanmadan önce bazı varsayımlar göz önünde bulundurulmalıdır. Bu blog yazısında, çoklu doğrusal regresyonun ne olduğunu, varsayımlarını ve SPSS ile nasıl yapıldığını öğreneceksiniz.

DOĞRUDAN Regresyon Analizi Adımlarına Geçmek İçin TIKLAYIN

Çoklu Doğrusal Regresyon Nedir?

Çoklu doğrusal regresyon, bağımlı bir değişkenin bir veya daha fazla bağımsız değişken tarafından açıklanmaya çalışıldığı bir istatistiksel analiz yöntemidir. Değişkenlerin hepsinin devamlı veri tipinde olması gerekir. Çoklu doğrusal regresyon, bağımsız değişkenlerin bağımlı değişkeni nasıl etkilediğini belirlemek ve bağımsız değişkenlerin farklı olması durumunda bağımlı değişkenin alması gereken değeri tahmin etmek için kullanılır.

Çoklu doğrusal regresyon analizi için bazı varsayımlar vardır. İlk olarak, hata terimlerinin normal dağılıma sahip olması gerekmektedir. İkinci olarak, değişkenler arasında hata terimlerinin (bağımsız değişkenler arasında) homoscedasticity adı verilen sabit varyanslı bir ilişki olmalıdır. Ayrıca, bağımsız değişkenler arasında çoklu doğrusal ilişki olmaması da önemli bir varsayımdır. Bu varsayımların incelenmesi, çoklu doğrusal regresyon analizinin doğru ve güvenilir sonuçlar elde etmesine yardımcı olur.

SPSS ile Çoklu Doğrusal Regresyon Türleri

SPSS’te çoklu doğrusal regresyon analizi yaparken, birden fazla sayıda olan bağımsız değişkenleri regresyon modelinize ne şekilde, hangi sırayla eklediğiniz önemlidir. 3 adet farklı yöntemle bağımsız değişken ekleyebilirsiniz. Bunlar hiyerarşik, forced entry ve stepwise yöntemleridir.

1. Hiyerarşik Regresyon Analizi:

   • Hiyerarşik regresyon analizi, bağımsız değişkenleri modelinize eklemenin belirli bir sırayla yapılmasına dayanır.
   • Adım adım değişken eklenir ve her adımda modelin açıklama gücü (R²) kontrol edilir.
   • Analizin başlangıcında teorik olarak önemli olduğu düşünülen değişkenler eklenir.
   • Her adımda yeni bir değişken eklenir ve modelin performansı değerlendirilir.
   • Deney sonucundan spesifik belli bir beklenti varsa, bu yöntemin kullanılması tavsiye edilir.

2. Forced Entry Regresyon Analizi:

   • Forced entry regresyon analizinde, tüm bağımsız değişkenler aynı anda modele eklenir. Yani, tüm değişkenler aynı adımda zorlanmış bir şekilde modele dahil edilir.
   • Bu yöntemde, değişkenlerin teorik olarak önemli olup olmadığını değerlendirmek için bir ön analiz yapılmalıdır.
   • Deney sonucundan spesifik bir beklenti yoksa ve sadece hangi bağımsız değişkenlerin önemli olduğu keşfedilmek isteniyorsa, bu yöntemin kullanılması tavsiye edilir.

3. Stepwise Regresyon Analizi:

   • Stepwise regresyon analizi, bağımsız değişkenleri teker teker modelde bırakma veya çıkarma kararıyla birlikte gerçekleştirilir.
   • Her adımda modele dahil edilecek, modelde kalacak veya çıkacak değişkenler istatistiksel kriterlere dayanarak belirlenir.
   • Stepwise regresyon, otomatik olarak değişken seçimi yapar, ancak bu yöntemde overfitting (modelde aşırı uyum) riski vardır.
   • Bu yöntem saf olarak matematiğe dayanır. Araştırmalarda kullanılması fazla tavsiye edilmez. Bu yöntem yerine Hiyerarşik veya Forced Entry yöntemlerinin kullanılması daha sağlıklıdır.

Çoklu Doğrusal Regresyon Varsayımları

SPSS’te yapacağımız çoklu doğrusal regresyon analizinde bulduğumuz sonuçlara güvenebilmemiz için, verimizin regresyon analizi öncesinde bazı varsayımları sağlıyor olması gerekir. Bu varsayımlar şunlardır. Varsayımları burada listeleyip, bir sonraki başlığın altında SPSS ile nasıl bakılacağını tarif edeceğim.

1. Bütün bağımsız ve bağımlı değişkenlerin devamlı veri tipinde olması gerekir.
2. Bağımlı değişkenin (ya da daha iyisi Residual’ların) normal dağılım göstermesi gerekir.
3. Veride outlier yani uç değer olmaması gerekir.
4. Her bağımsız değişken, tek başına ele alındığında, eğer bağımlı değişkenle 0.30’dan fazla korelasyon gösteriyorsa, bu korelasyonun şekli doğrusal yani lineer olmalıdır.
5. Bağımsız değişkenlerin herhangi ikisini ele aldığımızda, bu iki değişkenin birbiriyle 0.70’ten fazla korelasyon göstermemesi gerekir. (Çoklu Doğrusallık Varsayımı)

SPSS ile Çoklu Doğrusal Regresyon Varsayımları Test Etme

Normalde istatistiksel testlerde önce varsayımları kontrol edip ondan sonra testi yapmaya başlıyorduk. Çoklu doğrusal regresyon varsayımlarını ise, regresyonu yaptıktan sonra tabloları okuyarak ve üzerine bir-iki ayrı küçük test yaparak kontrol ediyoruz. Bu yüzden hemen aşağıdaki başlığı tamamen takip ederseniz, hem çoklu regresyon yapma adımlarını, hem de varsayım test etme adımlarını birlikte göreceksiniz.

SPSS ile Çoklu Doğrusal Regresyon Nasıl Yapılır?

Bu sayfadaki örnekte, hiyerarşik çoklu regresyon metoduyla çoklu regresyon yapmayı göstereceğim. Eğer forced entry ya da stepwise regresyon metoduyla regresyon yapacaksanız bu sayfa yerine linklerdeki diğer ilgili sayfaları okumanızı öneririz.

SPSS’te çoklu doğrusal regresyon için aşağıdaki adımları takip edebiliriz.

Bu sayfada yapacağımız örnekte, 3 bağımsız, 1 bağımlı değişkenimiz var. Depresyon, dayanıklılık ve stres faktörlerinin, yorgunluk seviyesiyle ilişkisine bakacağız.

Analyze -> Regression -> Linear

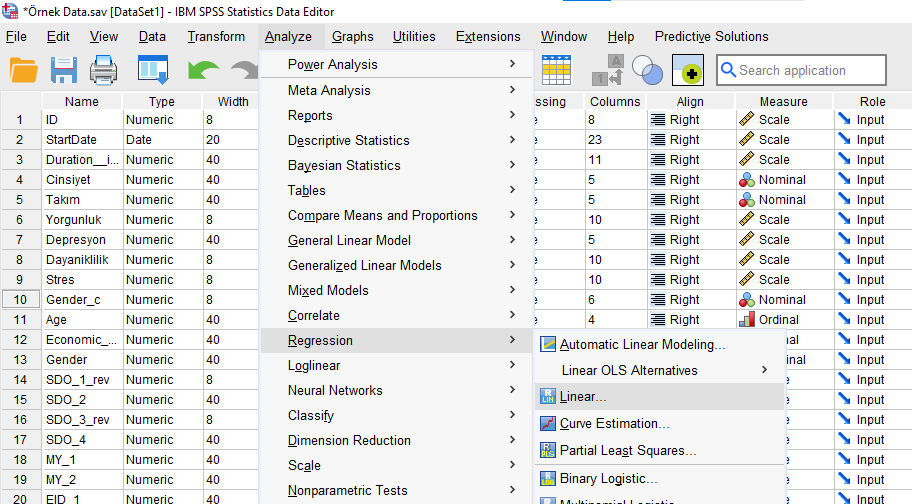
Açılan Linear Regression penceresinde, bağımlı değişkenimizi Dependent kutusuna koyuyoruz. Bağımsız değişkenlerimizden sadece 1 tanesini, Independent(s) kutusuna koyuyoruz. Bu kutunun altındaki “Method” kısmında “Enter” seçili olması lazım.

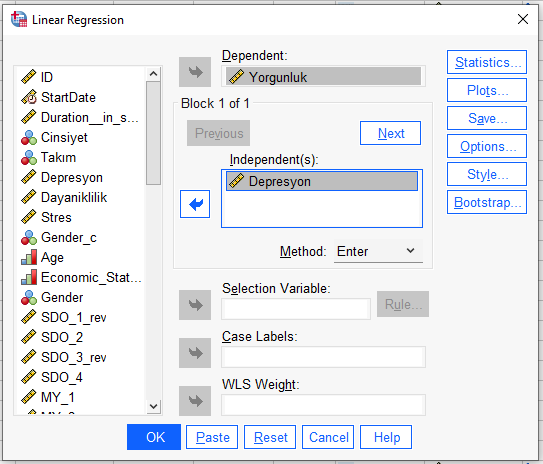
İlk değişkeni koyduktan sonra, “Next” butonuna basıyoruz ve Independent(s) kutusuna ikinci bağımsız değişkeni ekliyoruz.

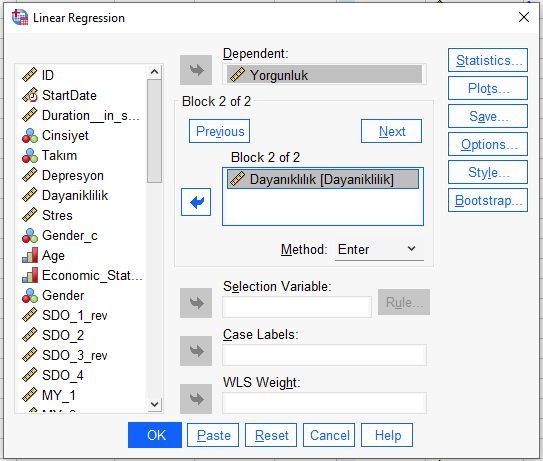
Sonra yine “Next”e basarak, üçüncü bağımsız değişkeni ekliyoruz. Bütün bağımsız değişkenleri eklemiş olana kadar böyle yapın.

Daha sonra, “Statistics” butonuna basarak, açılan yeni pencerede, aşağıdaki kutucukları işaretliyoruz. Sonra “Continue”ya basıyoruz.

“Plots”a basıp, “Produce all partial plots” seçeneğini işaretliyoruz. “Continue”ya basıyoruz.

“Save” butonuna basıp, açılan yeni pencerede Mahalanobis, Cook’s (bu ikisi sadece uç değer bulmamıza yardımcı olacak) ve Standardized Residuals (bunun üzerinden daha sonra normal dağılımı da test edeceğiz) seçeneklerini işaretliyoruz.

“Continue”ya basıyoruz.

Son olarak, “OK” butonuna basarak SPSS’te çoklu doğrusal regresyon analizimizi başlatıyoruz.

Çoklu Doğrusal Regresyon SPSS Tablo Yorumlama

Çoklu doğrusal regresyon analizini başlattıktan sonra, SPSS bize bir sürü tablo verecektir. Bu tabloları nasıl okumamız gerektiğini ve önceki yaptığımız adımların üzerine varsayım testlerini nasıl yapacağımızı aşağıda anlatıyorum.

SPSS’in sonuç tabloları penceresinde önce, en alttaki “Charts” bölümüne bakmalıyız. Burada, teker teker her bağımsız değişkenin bağımlı değişkenle olan korelasyon ilişkisi hakkında tablolar bulunmakta. Bizim 3 bağımsız değişkenimiz olduğu için 3 tablo var.

İlk tablonun üzerine çift tıklıyoruz.

Açılan yeni pencerede sağ alttan beşinci minik ikona basıyoruz.

Bu bize bir korelasyon çizgisi verdi. Tabloyu gözümüzle inceliyoruz. Eğer doğrusal bir durum varsa, korelasyona devam ediyoruz.

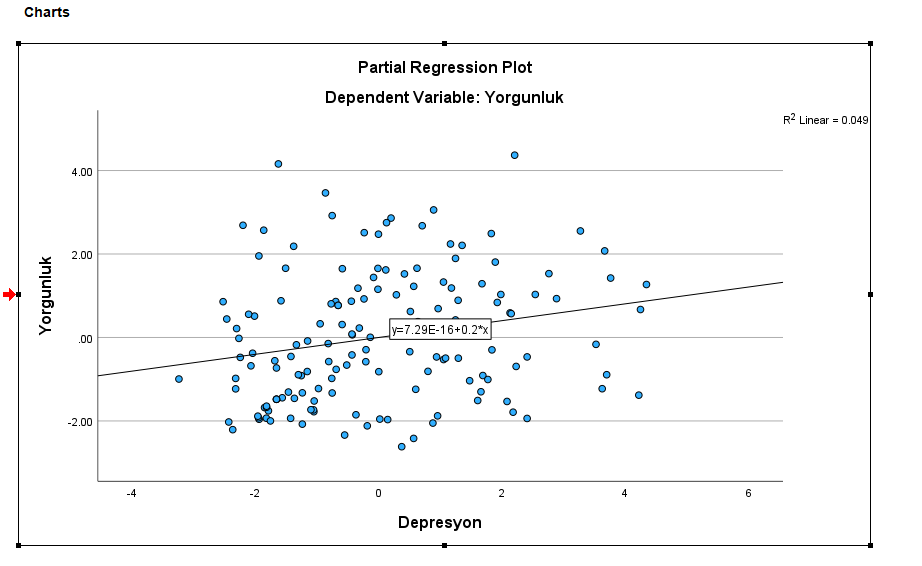
Aynı işlemi diğer iki grafik için de yapıyoruz.

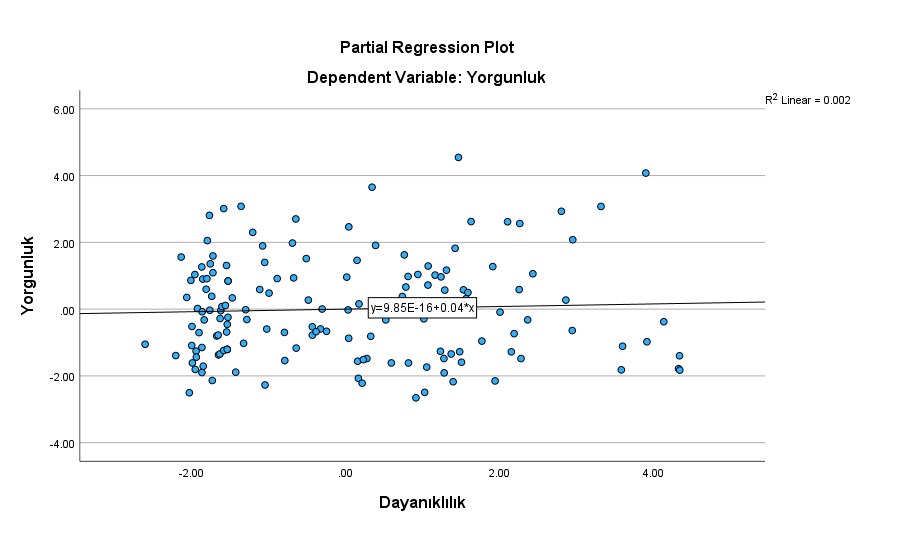
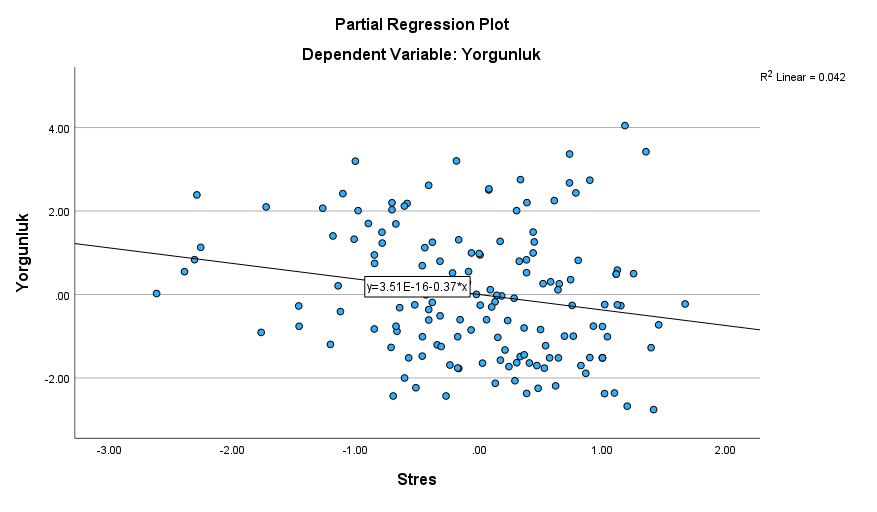
UYARI: Elde ettiğimiz grafiklerden herhangi biri, aşağıdaki resimde kırmızı çarpı işaretli grafiklere benzeseydi, bu, ilgili iki değişken arasında doğrusal ilişki olmadığı anlamına gelirdi.

Bir bağımsız değişkenin bağımlı değişkenle korelasyonu böyle bir grafik verdiyse, o bağımsız değişkeni çoklu regresyon analizinden çıkartıp, analizi aynı şekilde o değişken hariç en baştan yapmak daha doğru olacaktır.

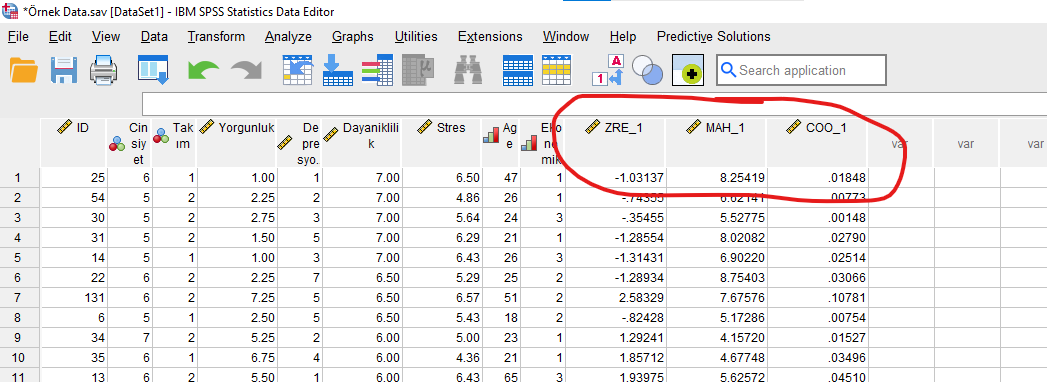
Varsayım Kontrol: Uç Değer Bulma

Varsayımlarımızdan biri, verimizde uç değer olmamasıydı. Şimdi verideki uç değerleri nasıl buluruz onu inceleyeceğiz.

SPSS veri setimizin en sağ tarafında, SPSS’in bize 3 tane yeni değişken oluşturduğunu göreceğiz. Veri setimizdeki her katılımcının hangi değere sahip olduğunu tablodan inceleyebiliriz.

ZRE_1 = Standardized Residual demektir. -3 ve +3 değerleri dışındaki değerler uç değerlerdir. Eğer -3 ve +3 arasında olmayan bir Standardized Residual değerine sahip katılımcı varsa, o katılımcı veriden çıkartılıp, çoklu regresyon analizi aynı şekilde baştan tekrar yapılmalıdır.

MAH_1 = Mahalanobis Uzaklığı demektir. Bir değerin uç bir değer olduğunu gösteren Mahalanobis uzaklığı eşik değeri, veri setinin büyüklüğüne göre değişiyor. Basitçe yuvarlak bir hesap yöntemiyle:

• Örneklem büyüklüğümüz 500, 5 tane bağımsız değişkenimiz var ise => 25’ten büyük değerler problematik
• Örneklem büyüklüğümüz 100, 3 tane bağımsız değişkenimiz var ise => 15’ten büyük değerler problematik
• Örneklem büyüklüğümüz 30, 2 tane bağımsız değişkenimiz var ise => 11’den büyük değerler problematik

Problematik olan veriler, veri setinden çıkartılıp çoklu regresyon analizi en baştan tekrar yapılmalıdır. Veri setiniz yukarıdaki örneklere tam olarak uymuyorsa, bunların arasında göz kararı bir eşik değeri belirlemeye çalışın. Mahalanobis Uzaklığı hakkında daha detaylı bir yazıyı yine bu web sitesinde bulabilirsiniz.

COO_1 = Cook’s Distance demektir. -1 ve +1 değerleri dışındaki değerler uç değerlerdir. Eğer -1 ve +1 arasında olmayan bir Cook’s Distance değerine sahip katılımcı varsa, o katılımcı veriden çıkartılıp, çoklu regresyon analizi aynı şekilde baştan tekrar yapılmalıdır. Cook’s Distance hakkında daha detaylı yazımı okumak için linke tıklayın.

Varsayım Kontrol: Normal Dağılım Bulma

Çoklu doğrusal regresyon varsayımlarımızdan ikincisi, verimizdeki Residual’ların normal dağılım göstermesiydi. Bu önemli bir varsayımdır. Bunu, SPSS’in bize oluşturduğu ZRE_1 yani Standardized Residual üzerinden test edeceğiz.

Analyze -> Descriptive Statistics -> Explore basıyoruz.

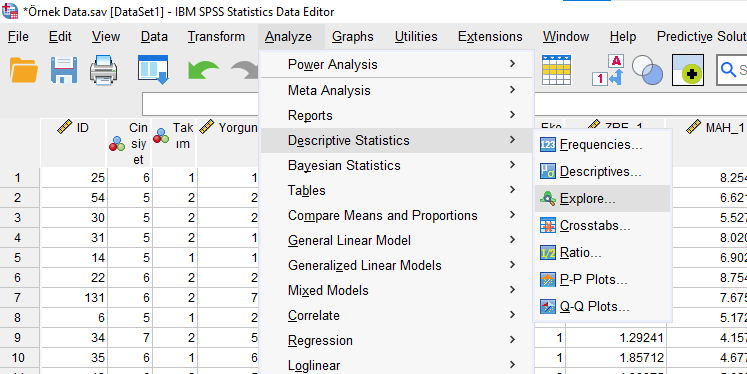
Açılan pencerede, ZRE_1 değişkenimizi Dependent List penceresine atıyoruz.

Plots’a basıp, aşağıdaki seçenekleri seçiyoruz.

Continue ve OK’a basıyoruz. SPSS bize yeni tablolar sunacak.

“Tests of Normality” tablosunda, Sig. değerlerine bakıyoruz. Shapiro-Wilk tarafındaki Sig. değerine bakmak genelde daha iyi. Bu tablodaki Sig. yani p değeri 0.05’ten büyükse, normallik varsayımı doğrulanmıştır diyebiliriz.

Eğer 0.05’ten küçükse ve diğer yöntemlerle de normal dağılım olduğuna yönelik bir işaret bulamıyorsak, çoklu doğrusal regresyon yerine teker teker ikili non-parametrik (veya uygunsa parametrik) korelasyon analizleri yapmamız daha uygun olacaktır.

Eğer 0.05’ten küçük veya yakın bir değer çıktıysa, normallik testi ile normal dağılım olup olmadığına nasıl karar verebileceğimiz hakkında detaylı yazımı okumanızı öneririm.

Bu örnekte Sig. yani p değerlerinin ikisi de 0.05’in üzerinde, sorun yok.

Normal dağılım varsayımı, çoklu doğrusal regresyon varsayımları arasında, ihlal edilmesi en az problem yaratan varsayım olarak görülür. Bu sayfada anlattığım diğer varsayımların ihlal edilmesi, normal dağılımın ihlal edilmesinden daha büyük problem yaratır. O yüzden çoklu doğrusal regresyonda normal dağılıma birazcık bile yakın bir dağılıma sahip isek sorun yok diyebiliriz.

Varsayım Kontrol: Çoklu Doğrusallık Bulma (Multicollinearity)

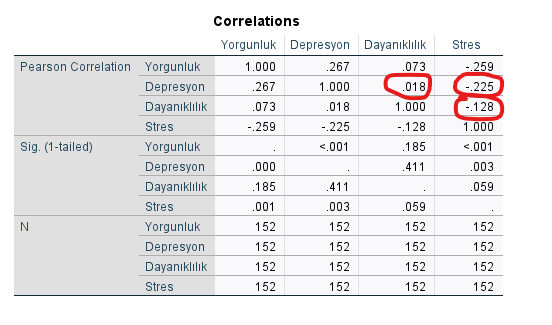
Bağımsız değişkenlerin ikisinin birbiriyle 0.70’ten fazla korelasyon göstermemesi gerekiyor demiştik. Bunu 2 tabloyu ayrı ayrı inceleyerek belirliyoruz.

“Correlations” tablosunda, bağımsız değişken çiftlerinin hepsi için Pearson Correlation miktarına bakıyoruz. Bu örneğimizde “Depresyon & Dayanıklılık”, “Depresyon & Stres” ve “Dayanıklılık & Stres” çiftlerinin Pearson korelasyon miktarlarının 0.70’ten büyük olmaması gerekiyor. Neyse ki hiçbiri büyük değil.

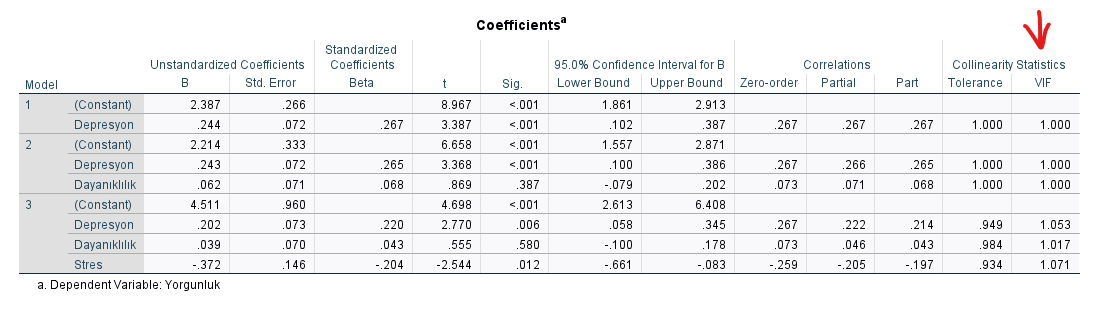
Çoklu doğrusallığı bir de Variance Inflation Factor (VIF) denen bir değer üzerinden test edebiliriz. Bunun için, SPSS tabloları arasından “Coefficients” başlıklı tablonun en sağdaki VIF isimli sütununa bakıyoruz.

Eğer değişkenlerden ikisinin VIF değerinin 10’dan büyük olduğunu görüyorsanız, o iki bağımsız değişken birbiriyle yüksek doğrusal korelasyona sahip demektir. Bu iki değişkenin bir tanesi veri setinden çıkartılıp, çoklu doğrusal regresyon analizi o değişkensiz tekrar baştan yapılmalıdır.

Varsayımların hepsini buraya kadar yaptığımız işlemlerde test etmiş olduk. Buraya kadar yaptığımız varsayım testleri önemliydi, çünkü varsayımları doğrulamış olmamız çoklu doğrusal regresyon analizinin sonuçlarının güvenilir olmasını sağlamaktadır.

Şimdi asıl çoklu doğrusal regresyon sonuçlarını incelemeye başlayalım.

Çoklu doğrusal regresyon SPSS tablolarında birçok tabloda, eğer 3 bağımsız değişken varsa 3 ayrı satırda 3 ayrı model gösterilir. (5 bağımsız değişken varsa 5 model gösterilir). İlk model sadece 1 değişkenin modele sokulmasıyla, ikinci model 2 değişkenin birlikte modele sokulmasıyla, üçüncü model ise 3 değişkenin hep birlikte modele sokulmasıyla elde edilen modeldir.

Bizim örneğimizde:

1. Birinci model sadece Depresyon’un Yorgunluk üzerindeki etkisine bakan model.
2. İkinci model Depresyon ve Dayanıklılık’ın Yorgunluk üzerindeki birlikte etkisine bakan model.
3. Üçüncü model Depresyon, Dayanıklılık ve Stres’in Yorgunluk üzerindeki birlikte etkisine bakan model.

En önemli model üçüncü modeldir ama diğer modellere de bakarak anlamaya çalışmak, çoklu regresyon analiz sonuçlarını anlamamıza yardımcı olur.

ANOVA Tablosu

ANOVA tablosundaki Sig. değeri, p değeridir. Bu değer, SPSS’in kurduğu regresyon modelinin, rastgele bir dağılımdan anlamlı şekilde farklı olup olmadığını belirlemeye yarar. Eğer p değeri 0.05’ten küçükse, bağımsız değişkenlerden en az 1 tanesinin bağımlı değişken ile arasında anlamlı bir korelasyon ilişkisi var demektir.

İlk satırdaki p değeri, tek bağımsız değişkenin modele sokulmasıyla yapılan regresyon analizinin anlamlılık değeridir. Son satırdaki p değeri de bütün bağımsız değişkenlerin birlikte modele sokulmasıyla yapılan regresyon analizinin anlamlılık değeridir. Son satırdaki p değerine bakmamız en önemlisidir. Eğer bu değer 0.05’in altında ise, regresyon modelimiz istatistiksel olarak anlamlı demektir.

Bu örnekte 0.05’in altında bir p değeri bulduk. Şimdi, bağımlı değişken acaba hangi bağımsız değişkenlerle korelasyon gösteriyor ona bakalım.

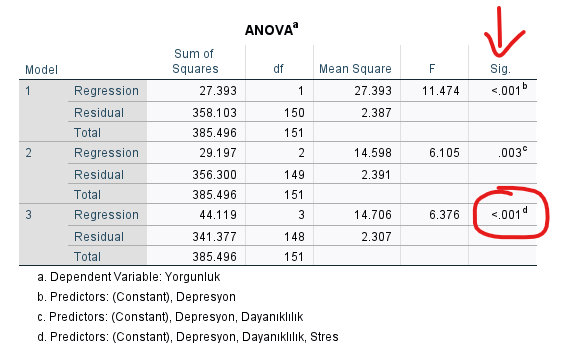
Modellerin Karşılaştırılması

Aşağıdaki “Model Summary” tablosunda kırmızı yuvarlak içine aldığımız yerlere bakalım.

R Square, R Kare demektir ve modelin değişkenler arasındaki ilişkiyi açıklama gücünü ifade eder. R Square Change, modele sokulan her yeni değişkenin modelin açıklama gücünü ne kadar iyileştirdiğini gösterir. Sig F Change ise açıklama gücünün iyileştirilme miktarının istatistiksel olarak anlamlı olup olmadığını belirlemeye yarar.

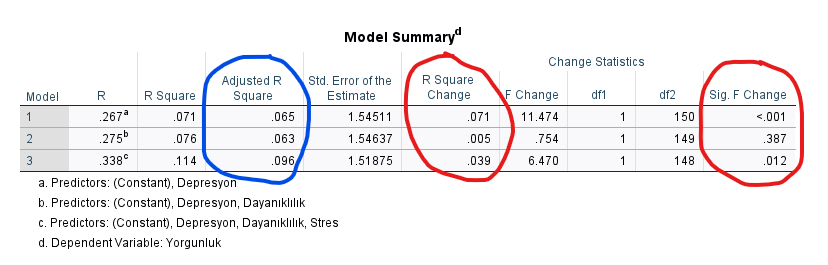
Bu örnekteki tabloyu inceleyecek olursak, Depresyon’un regresyon modeline dahil edilmesi, istatistiksel olarak anlamlı bir şekilde (çünkü 1. satır için p < 0.001) R Kare’yi değiştirmiş. Dayanıklılık’ın regresyon modeline dahil edilmesi, istatistiksel olarak anlamlı bir şekilde (çünkü 2. satır için p = 0.387) R Kare’yi değiştirmemiş. Stres’in regresyon modeline dahil edilmesi, istatistiksel olarak anlamlı bir şekilde (çünkü 1. satır için p = 0.012) R Kare’yi değiştirmiş. Yani buradan, Depresyon ve Stres, bağımlı değişken olan Yorgunluk ile anlamlı bir ilişkiye sahiptir sonucunu çıkartabiliriz. Dayanıklılık’ın ise Yorgunluk ile istatistiksel olarak anlamlı bir ilişkisi yokmuş.

Bunun sağlamasını R Square Change değerlerine bakarak da yapabiliriz. Depresyon, modeldeki R Kare değerini 0.071 miktarında arttırmış. Sonra modele eklediğimiz Dayanıklılık, modeldeki R Kare’yi sadece 0.005 arttırmış. Modele en son eklediğimiz Stres ise, modeldeki R Kare’yi 0.039 arttırmış. Bu tablodaki Sig. değerlerine bakarak da hangi R Kare artışlarının istatistiksel olarak anlamlı olduğunu görmüş olduk.

Mavi yuvarlak içine aldığım Adjusted R Square değeri, modelin, bağımlı değişkenin değişiminin yüzde kaçını açıkladığını bulmamızı sağlar. Örneğin Model 3 için Adjusted R Square 0.096 çıkmış. Bu, Depresyon, Dayanıklılık ve Stres’ten oluşan bağımsız değişkenlerin, Yorgunluk bağımlı değişkeni üzerindeki değişimin %9.6’sını açıkladığı anlamına gelir. Yorgunluk üzerindeki kalan %90.4’lük değişim, bu modelde olmayan bilinmeyen başka faktörlere bağlıdır.

Regresyon Korelasyon Miktarları

Bu tabloda, en çok değişkenin dahil edildiği en son modeldeki bilgileri incelemekte fayda var.

Sig. değeri yani p değeri, her bağımsız değişkenin, bağımlı değişkendeki değişim üzerinde önemli bir etkisi olup olmadığı bilgisini verir. Eğer p değeri 0.05’ten küçük ise anlamlı demektir. Bu örnekte Depresyon ve Stres, bağımlı değişken olan Yorgunluk üzerinde anlamlı bir değişime sebep olmakta (çünkü p değerleri sırayla 0.006 ve 0.012), fakat Dayanıklılık Yorgunluk üzerinde anlamlı bir değişime sebep olmuyor (çünkü p değeri 0.580).

B değeri, her bağımsız değişkenin ölçüldüğü ölçekteki 1 birimlik değişimin, bağımlı değişken üzerinde kaç birimlik değişime sebep olduğunu söylüyor. Örneğin Depresyon’daki 1 birimlik değişim, Yorgunluk’ta 0.202 miktarda bir artışa sebep oluyor. Stres’teki 1 birimlik değişim, Yorgunluk’ta 0.372 miktarda azalışa sebep oluyor. Dayanıklılık’taki değişimin p değeri istatistiksel olarak anlamsız olduğu için (p değeri 0.05’ten büyük diye) bu değişkendeki değişimin Yorgunluk’ta ne kadar değişime sebep olduğunu bakmıyoruz.

Beta ise, farklı değişkenlerin ölçeklerinin standardize edilmesiyle bulunan bir değerdir. Burada, değerlerin kendisi değil de standart sapmaları üzerinden bir yorumlama yapılmaktadır. Beta değerleri şöyle okunur: “Depresyondaki değerde 1 standart sapmalık artış, Yorgunlukta 0.220 standart sapmalık artışa sebep olur; Stresteki 1 standart sapmalık artış, Yorgunlukta 0.204 standart sapmalık azalışa sebep olur”.

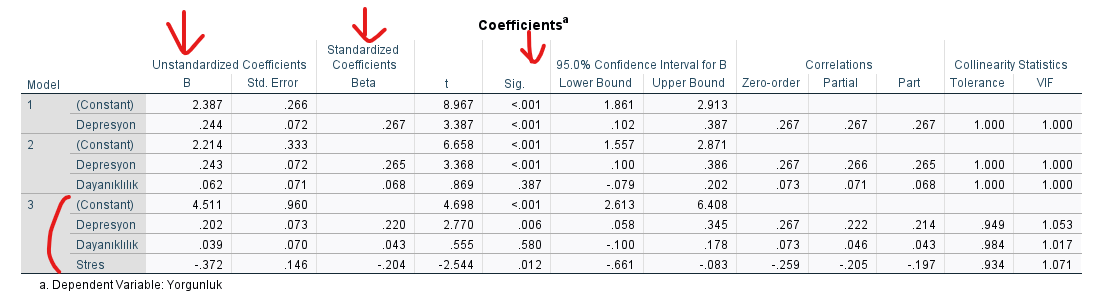
Sonuç olarak, Depresyon, Dayanıklılık ve Stres bağımsız değişkenlerinden Depresyon arttıkça Yorgunluk artarken Stres arttıkça Yorgunluk azalmaktaymış, Dayanıklılık ise Yorgunluk üzerinde bir etkiye sahip değilmiş. Artık bulduğumuz değerleri raporlama aşamasına geçebiliriz.