SPSS ile Kruskal-Wallis Testi (Resimli)

Kruskal-Wallis Testi, ANOVA varsayımlarının sağlanamadığı durumlarda, farklı grupların test skorlarını karşılaştırmak için kullanılan bir istatistiksel testtir. SPSS programıyla Kruskal-Wallis Testi yapmak oldukça kolaydır. Bu yazıda, Kruskal-Wallis Testi’nin ne olduğunu ve SPSS programında nasıl yapıldığını detaylarıyla öğreneceksiniz.

Kruskal-Wallis Testi Nedir?

Kruskal-Wallis testi, 3 veya daha fazla grup arasındaki farklılıkları değerlendirmek için yapılan bir non-parametrik (yani parametrik olmayan) testtir. Kruskal-Wallis testi, 3 veya daha fazla sayıdaki gruplar arasındaki test puanı farkını incelemek için Tek Yönlü ANOVA testinin non-parametrik bir alternatifi olarak kullanılabilir.

Eğer 3+ grubun bir test sonucu ortalama puanları karşılaştırılmak isteniyorsa fakat ANOVA varsayımları karşılanamıyorsa (mesela grupların normal dağılıma sahip olmaması en sık yaşanan ANOVA varsayım ihlalidir), grupları karşılaştırmak için ANOVA yerine Kruskal-Wallis testi uygulamak uygun olacaktır.

Ayrıca Kruskal-Wallis Testi, ANOVA’nın aksine, ordinal veri ile de çalışabilmektedir. Hem ordinal, hem de sürekli veri tipindeki veriler ile Kruskal-Wallis Testi yapmak mümkündür. (ANOVA testi yalnızca sürekli veri ile yapılabilmektedir.)

Mesela, 4 takım taraftarlarının (GS, FB, BJK, TS) maç sırasında bağırma miktarlarını karşılaştırmak istiyorsak ve ANOVA testi varsayımları doğrulanamadıysa o zaman Kruskal-Wallis testini kullanarak hangi takımların taraftarları hangi diğer takım taraftarlarından daha çok bağırıyor bunu öğrenebiliriz.

Kruskal-Wallis Testi Varsayımları

Bir non-parametrik test olması yüzünden, Kruskal-Wallis testi, parametrik testlerin aksine, sonuçların güvenilir olarak doğru yorumlanabilmesi için bağımlı değişkenin normal dağılım göstermesine ihtiyaç duymaz.

Bazı istatistikçilere göre, grupların homojen varyanslara sahip olmadığı durumlarda Kruskal-Wallis testinin kullanılmaması gerekmektedir. Fakat, tek adımda varyans homojenliğini test etmeye yarayan Levene Testi, normal dağılım göstermeyen veriler üzerinde uygulanamaz. Bu durumda normal dağılım göstermeyen (parametrik olmayan) verilerin varyans homojenliğini farklı bir şekilde test etmek gerekir, bu test de maalesef SPSS’te mevcut değildir. Bu yüzden, birçok sosyal bilimci, Kruskal-Wallis Testi’ni, grupların varyansları homojen olsa da olmasa da uygulamaktadır. Fakat, bunun en doğru yöntem olmadığını hatırlatalım. Parametrik olmayan veri için gruplar arası varyans homojenliğinin SPSS’te nasıl test edildiğini görmek için bu linkteki videoyu izleyebilirsiniz.

Eğer bağımsız değişken normal dağılmıyorsa ve gruplar arasında varyans homojenliği de sağlanmıyorsa, o zaman Medyan Testi yapmak Kruskal-Wallis Testi yapmaktan daha doğru bir uygulama olacaktır.

Kruskal-Wallis testi yapabilmek için karşılaştırdığınız 2 grubun üyelerinin tamamının birbirinden farklı kişilerden oluşuyor olması gerekir. Ayrıca Kruskal-Wallis testi uygulamak için verilerin ya sıralı ya da sürekli veri tipine sahip olması gerekir. Grupların birbirine yakın sayıda kişiden oluşuyor olması iyi olur ama kesin şart değildir.

SPSS ile Kruskal-Wallis Testi Nasıl Yapılır?

Bu örnekte 3 tane cinsiyetin (heteroseksüel erkek, heteroseksüel kadın, LGBT+) bir anket sonucu belirlenen stres skorlarını karşılaştırıyoruz. SPSS ile Kruskal-Wallis testi yaparak acaba bazı cinsiyetlerin stres skorları diğerlerinden anlamlı derecede farklı mı bunu öğreneceğiz.

Aşağıdaki adımları uygulayarak SPSS’te Kruskal-Wallis Testi yapılabilir.

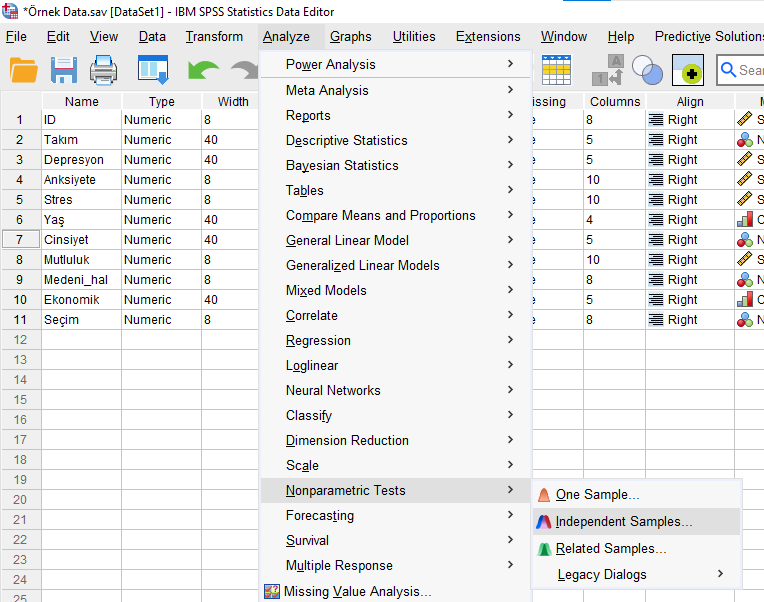
Analyze -> Nonparametric Tests -> Independent Samples

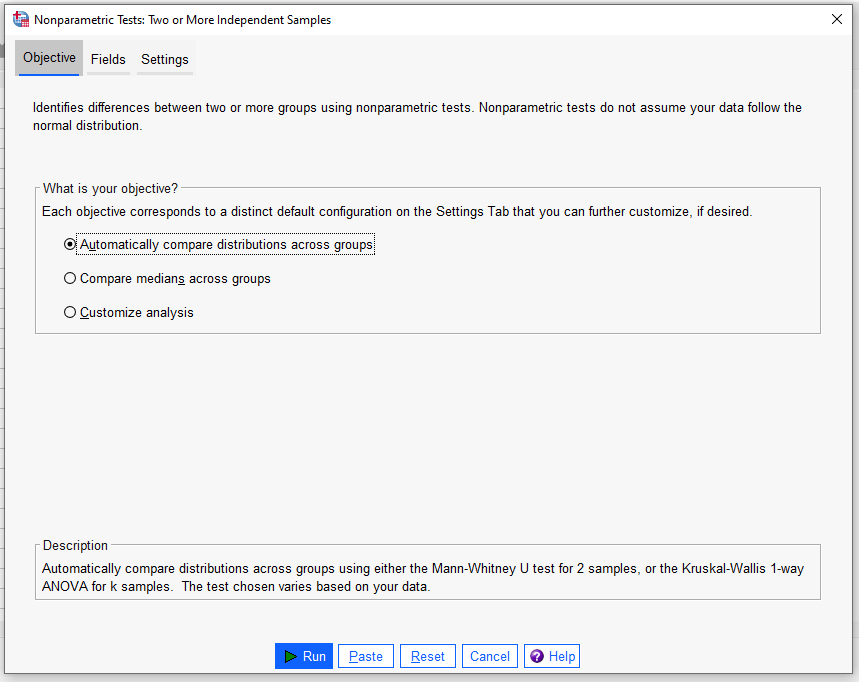
Açılan pencere 3 kısımdan oluşuyor. Objective kısmı bu şekilde görünmeli.

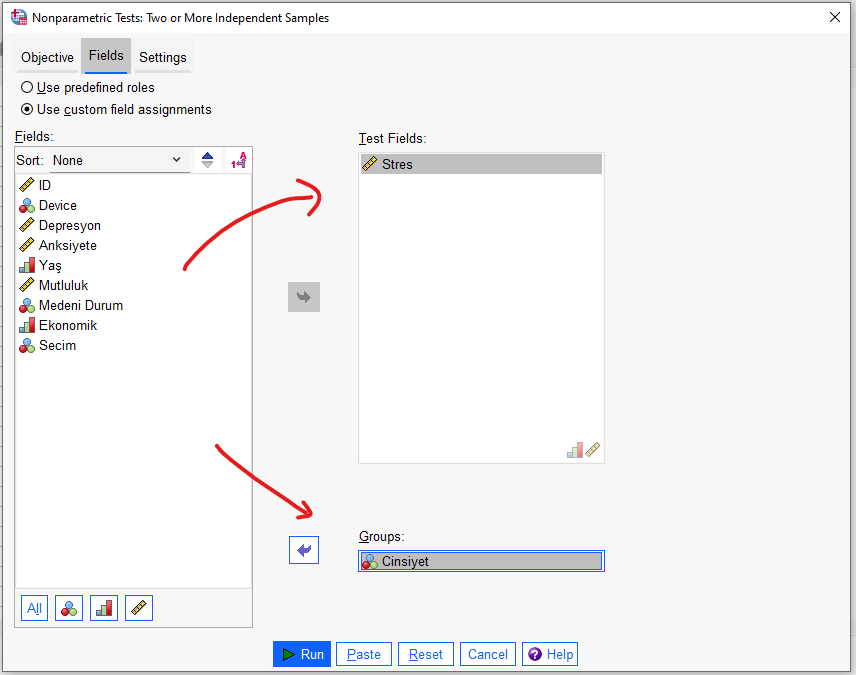
Fields kısmında, bağımlı değişkenimizi Test Fields kutusuna koyuyoruz. Bağımsız değişkenimizi de Groups kısmına koyuyoruz.

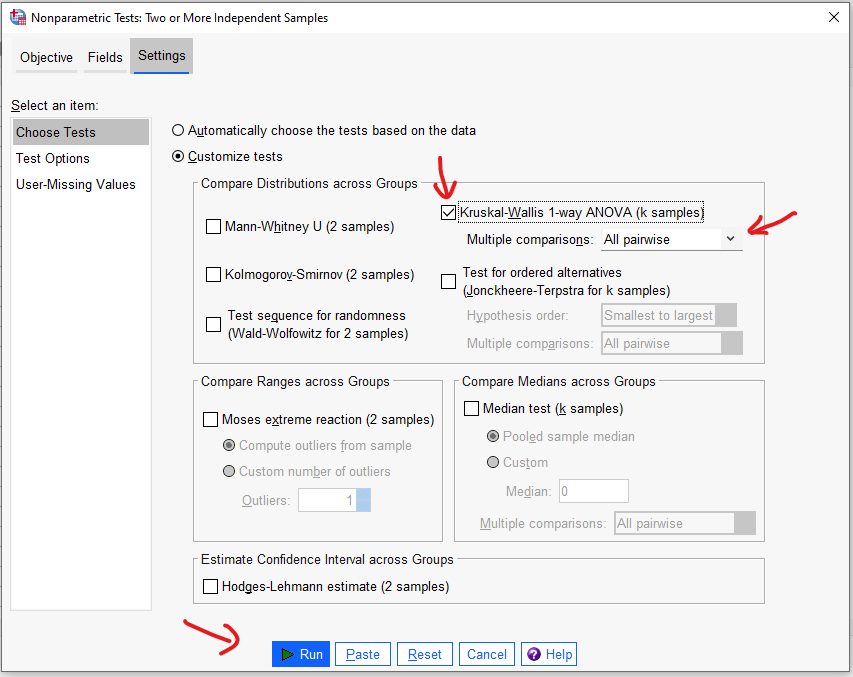
Settings kısmında, “Kruskal-Wallis 1-way ANOVA (k samples)” yazan yere ait kutucuğu işaretliyoruz. Aynı zamanda altındaki alan “Multiple comparisons: All pairwise” olarak seçili olmalıdır.

Sonra “Run” butonuna basarak, analizi başlatabiliriz.

Kruskal-Wallis Testi Yorumlama

SPSS bize birtakım tablolarla grafikler verecek. İlk bakmamız gereken yer, Summary tablosu. Burada kırmızı yuvarlak içine aldığım Sig. değeri Kruskal-Wallis testimizin p anlamlılık değeridir. Bu örnekte p değeri 0.006 çıkmış, yani 0.05’ten küçük olduğu için, “Kruskal-Wallis testimiz istatistiksel olarak anlamlıdır” diyebiliriz. Yani bazı cinsiyetlerin Stres skorları başka cinsiyetlerden anlamlı derecede farklıdır.

Hangi cinsiyetlerin diğer cinsiyetlerden anlamlı bir şekilde farklı Stres skoruna sahip olduğunu bulmak için, bir sonraki Pairwise Comparisons tablosunu incelememiz gerekiyor.

Not olarak düşeyim, yukarıdaki tablodaki Test Statistic değerini deneydeki kişi sayısının 1 eksiğine bölünce, Kruskal-Wallis testinin etki büyüklüğünü buluyoruz. Bu örnekte 10.335/(152-1)=0.06844 yani bağımlı değişkendeki toplam varyansın %6.84’ü bağımsız değişkenlerle açıklanabiliyor demektir.

Pairwise Comparisons tablosunu incelemeden önce, aşağıdaki kutu grafiğinden her cinsiyetin ortalama, en küçük ve en büyük Stres skoru aralıklarını inceleyebiliriz. Erkeklerin Stres skorları, diğer cinsiyetlerden biraz daha yüksek görünüyor. LGBT+ bireylerin ise Stres skorları diğerlerinden biraz düşük duruyor. Cinsiyetler arası bu farkların hangilerinin istatistiksel olarak anlamlı farklar olduğunu grafiğin aşağısında Pairwise Comparisons tablosuna bakarak anlayacağız.

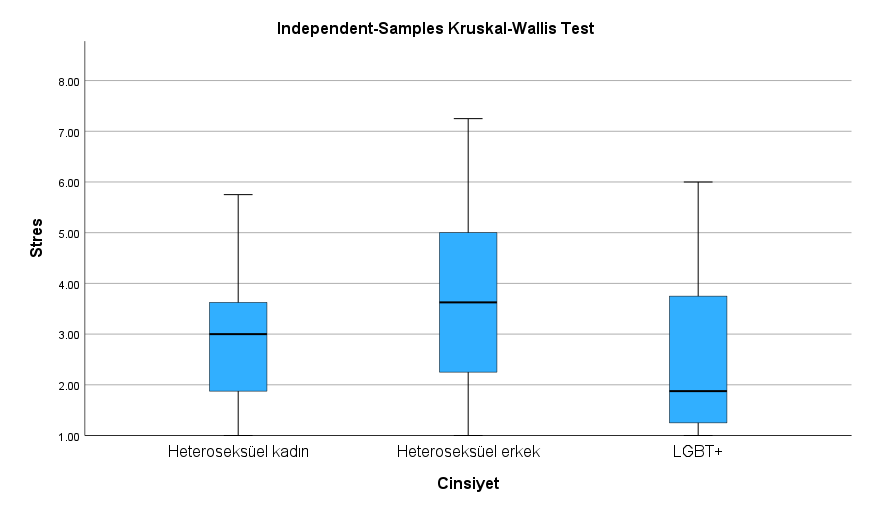
Pairwise Comparisons tablosunda, sırayla her cinsiyetin diğer bir cinsiyetle Stres skoru karşılaştırılıyor ve anlamlı bir fark var mı diye bulunuyor. Bu örnekte 3 cinsiyetimiz olduğu için, SPSS 3 farklı karşılaştırma yaptı.

Bu karşılaştırmaların hangilerinin istatistiksel olarak anlamlı olduğunu bulmak için, düz Sig. yerine en sağ sütundaki Adj. Sig değerine bakarak p değerini incelemek gerekmektedir. Çünkü aynı ikili karşılaştırma istatistiksel testini 3 kere yapınca, Tip I hata oranı artmaktadır (gerçekte var olmayan bir gruplar arası farkı varmış gibi görme ihtimali). Adj Sig. sütununda bir Bonferroni düzeltmesi yapılır ve eşik p anlamlılık değeri 0.05’te tutularak her karşılaştırma için yeni p değerleri hesaplanır.

• Bu örneğimizde, LGBT ve Kadın cinsiyetleri arasında istatistiksel olarak anlamlı bir Stres seviyesi farkı görülmemiş (çünkü p değeri 0.818).
• LGBT ve Erkek cinsiyetleri arasında istatistiksel olarak anlamlı bir Stres seviyesi farkı görülmüş (çünkü p değeri 0.014).
• Kadın ve Erkek cinsiyetleri arasında istatistiksel olarak anlamlı bir Stres seviyesi farkı görülmemiş (çünkü p değeri 0.052).

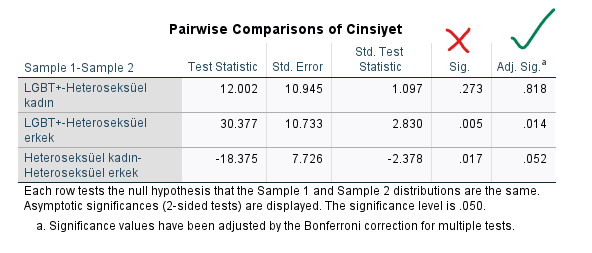
SPSS analizimiz ve tabloları yorumlamamız sonucunda şu sonuca varıyoruz: “Kruskal-Wallis Testi’ne göre Heteroseksüel Erkek katılımcılar, LGBT+ katılımcılardan istatistiksel olarak anlamlı biçimde daha yüksek Stres seviyesine sahiptirler. Diğer cinsiyetler arasında anlamlı bir Stres seviyesi farkı görülmemiştir.”

ÖNEMLİ NOT: Kruskal-Wallis testi sonucu istatistiksel olarak anlamlı yani 0.05’ten küçük bir p değeri bulduktan sonra hangi gruplar arası anlamlı Stres seviyesi farkı olduğunu görmek için karşılaştırma yapmaya post hoc karşılaştırma deniyor. Kruskal-Wallis testi için post hoc karşılaştırma yapmanın birden fazla yolu var.

1. Biz bu örnekte, Dunn’s Test kullanarak ikili karşılaştırmalar yaptık. Dunn’s Test en güvenilir olan Kruskal-Wallis post hoc testidir. Pairwise Comparisons tablosundaki Adj. Sig değerleri Dunn’s Test sonucu Bonferroni düzeltmesi uygulanarak gösterilmektedir, ve en güvenilir olan p değerleridir.
2. İkinci bir Kruskal-Wallis testi post hoc karşılaştırma yolu, Analyze -> Compare Means -> One Way ANOVA penceresinden Post Hoc’u seçip “Equal Variances Not Assumed” başlığı altındaki post hoc testlerinden birini seçmektir. Bunun en iyi yol olmama sebebi, ANOVA testiyle birlikte yapılıyor olmalarıdır. ANOVA yerine Kruskal-Wallis testi yapmamızı gerektirecek bir veri setimiz varsa post hoc testine de ANOVA post hoc testleriyle bakmamalıyız.
3. Üçüncü bir Kruskal-Wallis testi post hoc karşılaştırma yolu, Kruskal-Wallis testini yaptıktan sonra bütün cinsiyetlerin ikili kombinasyonlarının Stres seviyelerini Mann-Whitney U Testi ile test edip p değerlerine bakarak karar vermektir. Burada da, çok sayıda test yapıldığı için Tip I hata oranlarını azaltmak için p değerlerine sonradan hesap makinesiyle Bonferroni düzeltmesi uygulamak gerekmektedir. Bu yöntem yerine Dunn’s Test kullanırsak düzeltilmiş p değerleri otomatik görünecektir bu yüzden Kruskal-Wallis testinin post hoc analizini Mann-Whitney U Testi ile yapmak gereksizdir.