SPSS ile Faktöriyel ANOVA (Resimli)

Faktöriyel ANOVA, istatistiksel bir yöntemdir ve gruplar arasındaki farkların incelenmesi için kullanılan bir analiz yöntemidir. Bu blog yazısında, faktöriyel ANOVA’nın ne olduğunu, varsayımlarını ve SPSS ile nasıl yapıldığını ele alacağız. Yazının devamında, faktöriyel ANOVA sonuçlarının nasıl yorumlanması gerektiğini öğreneceksiniz. Faktöriyel ANOVA hakkında her şey bu rehberde.

Doğrudan ANOVA Yapma Adımlarına Geçmek İçin TIKLAYIN

Faktöriyel ANOVA Nedir?

Faktöriyel ANOVA, bir adet bağımlı değişkenin birden fazla bağımsız değişkenle ilişkisini incelemek için kullanılır. “Faktöriyel” terimi, birden fazla faktörün (bağımsız değişkenin) etkisinin bir arada değerlendirildiği anlamına gelir.

Faktöriyel ANOVA, genellikle iki veya daha fazla faktörün etkileşimini ve her bir faktörün bağımlı değişken üzerindeki etkisini anlamak amacıyla kullanılır. Bu analiz türü, deney tasarımlarında ve araştırmalarda faktörler arasındaki etkileşimleri ve tek başlarına etkilerini anlamak için yaygın olarak kullanılır.

Örneğin, bu sayfada yapacağımız faktöriyel ANOVA örneğinde, 3 adet bağımsız değişkenimiz olacak. Bunlar eğitim (ilkokul-lise-üniversite), şehir (İstanbul-Ankara), ve meslek (doktor-sanatçı-sporcu) olacak. Bağımlı değişkenimiz ise, maaş olacak. Eğitim, şehir ve mesleğin, maaşa ayrı ayrı ve birlikte etkilerini faktöriyel ANOVA analizi yaparak inceleyeceğiz.

Faktöriyel ANOVA Varsayımları Nelerdir?

Faktöriyel ANOVA’nın geçerliliği ve güvenilirliği sağlamak için bazı varsayımları vardır. Bu varsayımlar şunlardır:

1. Normallik Varsayımı:
   • Bağımlı değişkenin her bir grup içinde normal dağılıma sahip olması önemlidir. Bu, her bir faktör düzeyindeki gözlemlerin normal bir şekilde dağıldığı anlamına gelir. Normallik varsayımını test ederken, daha kısa süren fakat kesinliği daha az olan başka bir yöntem de, bağımlı değişkenin bütün veri setini tek grup olarak ele aldığımızda normal dağılım gösterip göstermemesidir. Bu örnekte daha az yer kaplaması açısından bunu uygulayacağız. Eğer normallik varsayımı doğrulanmaz ise, faktöriyel ANOVA yerine Kruskal-Wallis testi yapmak gerekecek.
2. Homojenlik Varsayımı:
   • Grupların varyansları arasında homojenlik olmalıdır. Yani, farklı faktör düzeyleri veya gruplar arasında gözlemlenen varyansların benzer olması gerekmektedir. Levene’nin homojenlik testi gibi istatistiksel testler kullanılarak bu varsayım kontrol edilebilir. Eğer bu varsayım Levene Testi yapılarak doğrulanmazsa bir tane faktöriyel ANOVA yapmak yerine her bağımsız değişken için ayrı ayrı Welch test‘ler yapmak gibi alternatifler tercih edilmelidir.
3. Bağımsızlık Varsayımı:
   • Gözlemlerin birbirinden bağımsız olması gerekmektedir. Bu, bir gözlemin bir grup içindeki diğer gözlemlerden bağımsız olduğu anlamına gelir.

Bu varsayımlar, Faktöriyel ANOVA sonuçlarının doğru ve güvenilir olmasını sağlamak için önemlidir. Varsayımların ihlali durumunda, analizin sonuçları güvenilir olmayabilir ve analizin yapıldığı veri setinin özelliklerine bağlı olarak düzeltici önlemler alınması gerekebilir. Varsayımların kontrol edilmesi, istatistiksel test sonuçlarının doğru bir şekilde yorumlanmasına yardımcı olur.

SPSS ile Faktöriyel ANOVA Normallik Varsayımı Nasıl Test Edilir?

Faktöriyel ANOVA normallik varsayımının doğruluğuna bakarken, bağımlı değişkenin normal dağılıp dağılmadığına bakmamız gerekiyor. Bunu, veri setinin tümünü tek bir grup olarak ele alarak yapabiliriz.

Eğer normal dağılım hakkında aklınızda soru işareti varsa, bu sayfaya devam etmeden önce sitemizdeki Normal Dağılımı Test Etmek başlıklı yazımıza bakıp bu sayfayı okumaya ondan sonra devam etmenizi öneririz.

Normallik Varsayımı Adım 1:

İlk önce SPSS’te Analyze -> Descriptive Statistics -> Explore butonlarına basıyoruz.

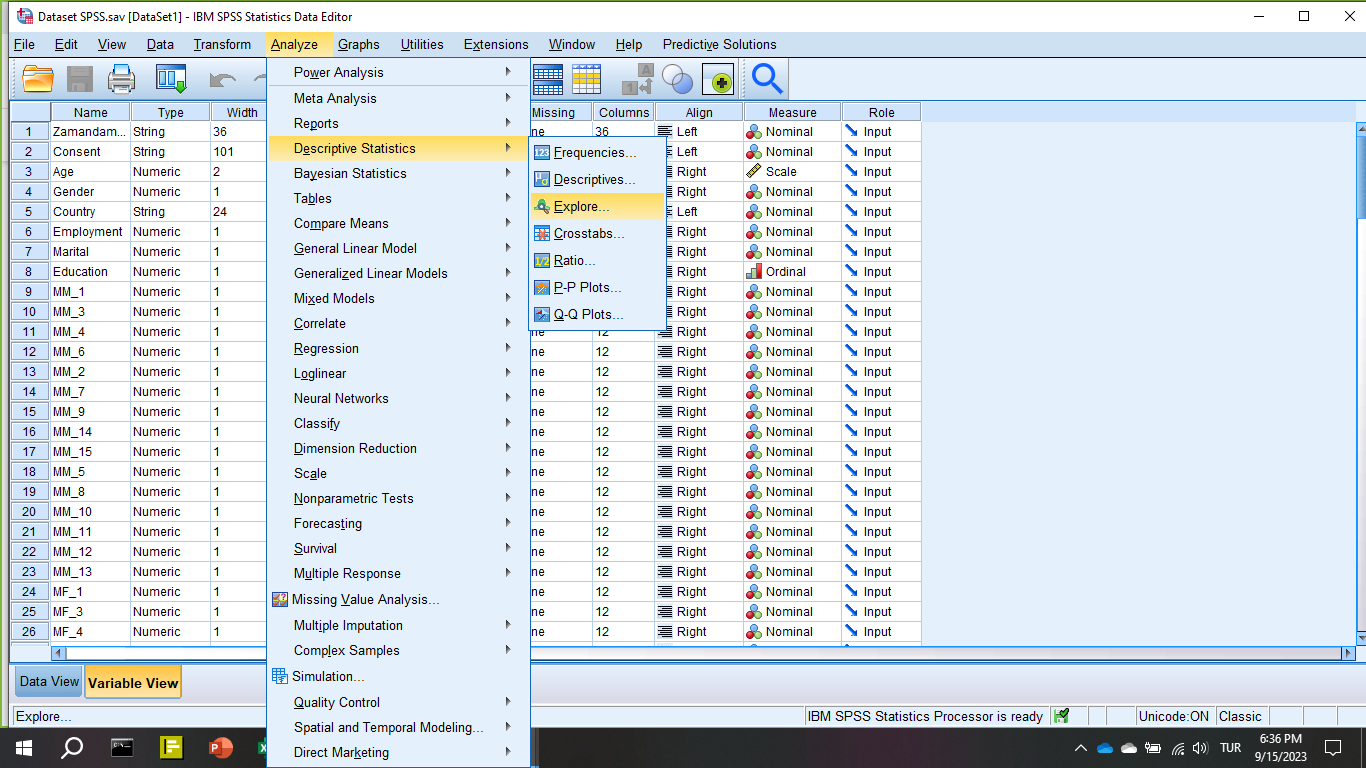
Normallik Varsayımı Adım 2:

Açılan yeni pencerede soldaki bölümden bağımlı değişkenimizi bulup sağ taraftaki Dependent List bölümüne atıyoruz. Sonra Plots butonuna basıyoruz.

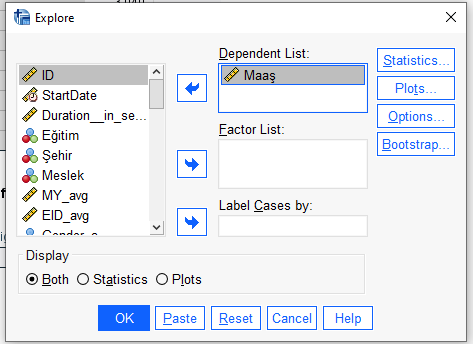
Normallik Varsayımı Adım 3:

Aşağıdaki resimde görüldüğü gibi, “Histogram” ve “Normality plots with tests” seçeneklerini işaretliyoruz. Continue’ya basıyoruz. Sonra OK tuşuna basıyoruz.

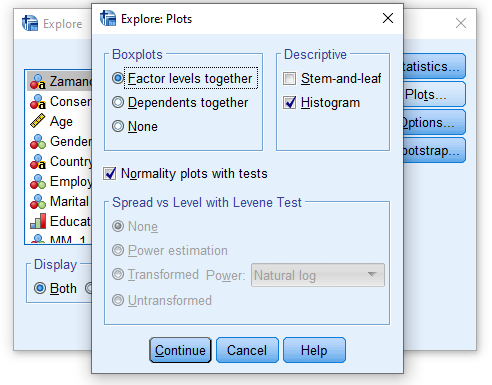
Normallik Varsayımı Adım 4:

SPSS yeni bir pencerede bize sonucu gösterecektir. Bu pencerenin adına Output deniyor. Output penceresinde “Tests of Normality” tablosuna bakmamız gerekiyor. Burada, Kolmogorov-Smirnov kısmındaki Sig. değerine veya Shapiro-Wilk kısmındaki Sig. değerine bakıyoruz. Bu değerler bize p değerini verir. Hangi kısımdaki değere baktığımız önemli. Eğer hangi kısımdaki değere bakacağınızdan emin değilseniz Normal Dağılımı Test Etmek konulu yazımıza bakabilirsiniz. Eğer Sig. değeri (yani p değeri) 0.05 değerinden büyük ise, normallik varsayımı doğrulanmış diyebiliyoruz.

Bu örnekte, normallik varsayımı doğrulandı, çünkü “Sig.” değerlerinin ikisi de 0.05’in üstünde.

SPSS ile Faktöriyel ANOVA Nasıl Yapılır?

Faktöriyel ANOVA’nın normallik varsayımını doğruladıktan sonra, SPSS ile faktöriyel ANOVA analizine başlayabiliriz.

Adım 1:

Analyze -> General Linear Model -> Univariate butonlarına tıklıyoruz.

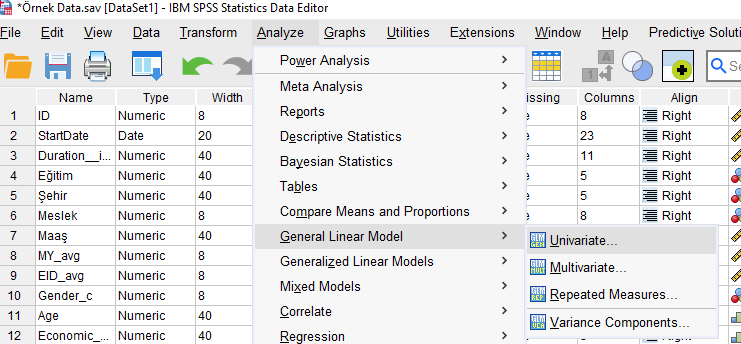
Adım 2:

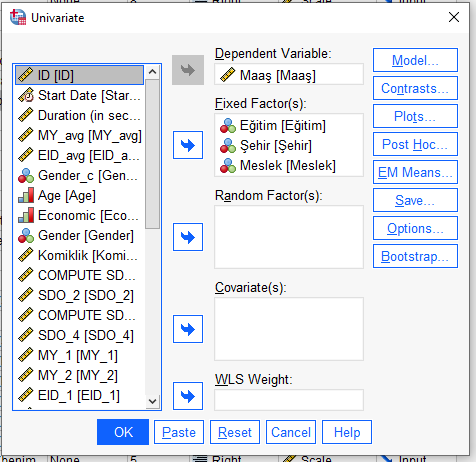
Bağımsız değişkenlerimizi (cinsiyet, şehir, meslek) soldaki kutudan alıp sağdaki “Fixed Factors” kutusuna yerleştiriyoruz.

Bağımlı değişkenimizi (maaş) soldaki kutudan alıp sağdaki “Dependent Variable” kutusuna yerleştiriyoruz.

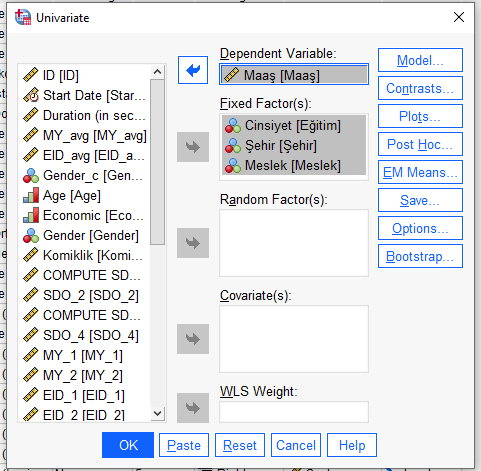
Adım 3:

“Post Hoc” butonuna basıyoruz. Bu test, bize 2’den fazla gruba ayrılan faktörlerin (mesela eğitim faktörü ilkokul, lise, üniversite olarak 3 gruba ayrılıyor) hangilerinin arasında anlamlı bir fark olduğunun tespitini yapmamız konusunda fayda sağlayacak.

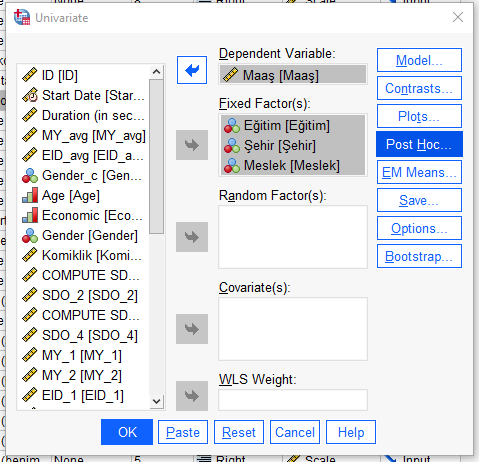
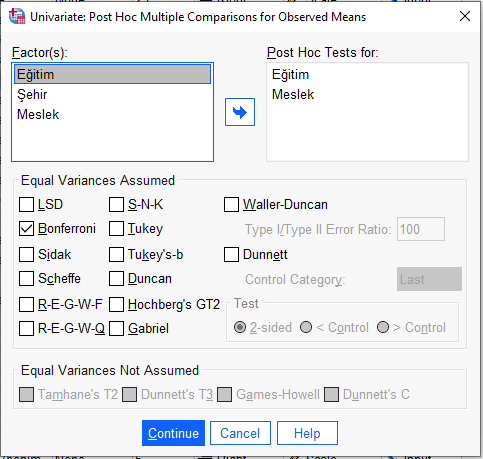
Eğitim ve Meslek değişkenlerini soldaki kutudan sağdaki kutuya alıyoruz. Şehir değişkenini almıyoruz çünkü bu değişkenin sadece 2 seviyesi var. Yani değişkenler arasında fark çıkarsa, hangi değişkenler arasında fark olduğu bariz. Fakat Eğitim ve Meslek değişkenlerinin 3’er seviyesi var (ilkokul, ortaokul, lise) ve (doktor, sanatçı, sporcu). Eğer bu gruplar arasında anlamlı bir fark çıkarsa, hangi gruplar arasında bu farkın olduğunu işte bu post hoc testi ile göreceğiz.

Daha sonra, ekranda görünen çok sayıda Post Hoc testinin arasından, bizim yapacağımız Post Hoc testini seçiyoruz. Farklı Post Hoc testlerinin avantajları ve dezavantajları birbirinden farklıdır, detaylı bilgi için Post Hoc testlerin karşılaştırılması hakkındaki yazımızı okuyabilirsiniz. Biz bu örnekte, araştırmalarda en çok kullanılan Post Hoc test olan Bonferroni testini seçtik ve onu işaretledik.

“Continue”ya basıyoruz.

Adım 4:

“EM Means” butonuna basıyoruz. Burası, bize farklı değişkenlerin birbiriyle etkileşime girdiğinde bağımlı değişkeni nasıl etkilediğini gösterecek.

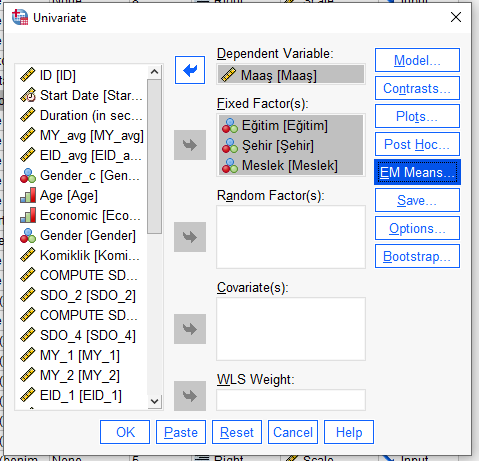
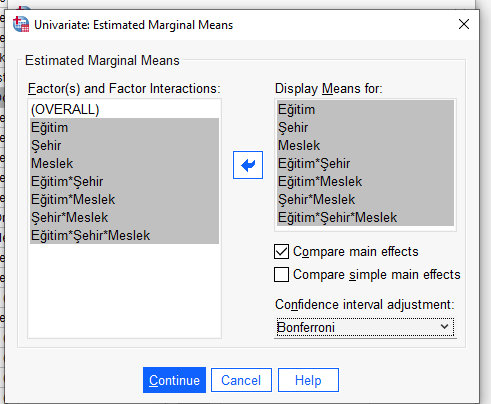
Soldan bütün değişkenleri alıp sağdaki kutuya atıyoruz.

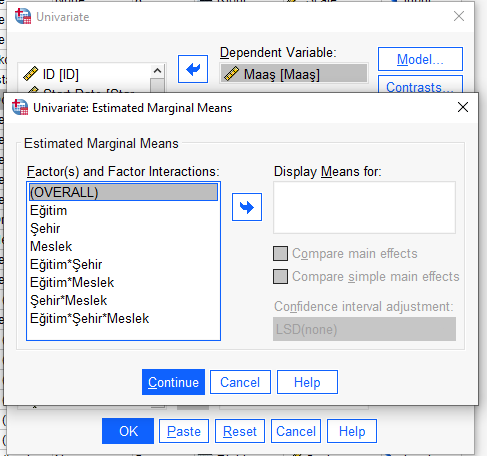
Attıktan sonra, “Compare main effects” seçeneğini işaretliyoruz. “Confidence interval adjustment” menüsünde, Bonferroni’yi seçiyoruz.

“Continue”ya basıyoruz.

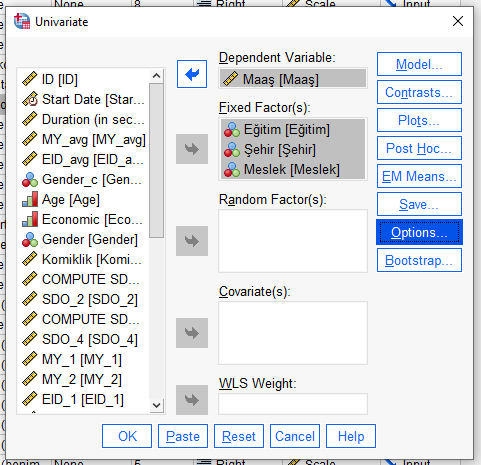
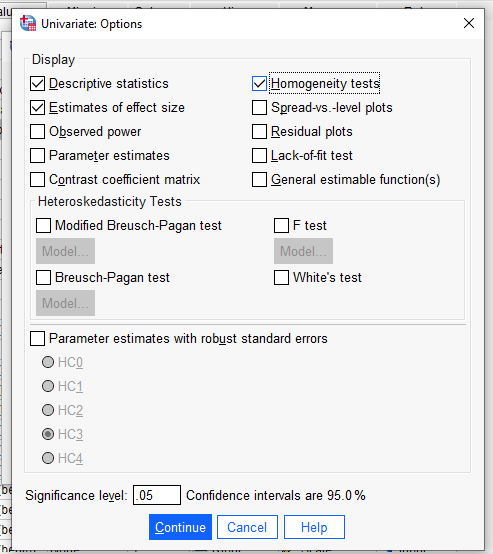
Adım 5:

“Options” butonuna tıklayıp, açılan menüden “Descriptive statistics”, “Estimates of effect size” ve “Homogeneity tests” seçeneklerini seçiyoruz. “Continue”ya basıyoruz.

Son Adım:

“Univariate” penceresinde, “OK” butonuna basıyor ve faktöriyel ANOVA analizimizi başlatıyoruz.

Faktöriyel ANOVA Tablo Yorumlama

SPSS’te faktöriyel ANOVA analizimizi yukarıdaki işlemleri yapıp başlattıktan sonra, karşımıza çeşitli tablolar ve grafikler gelecek. Bunların nasıl yorumlanacağına beraber bakalım.

Adım 1: Levene’s Test

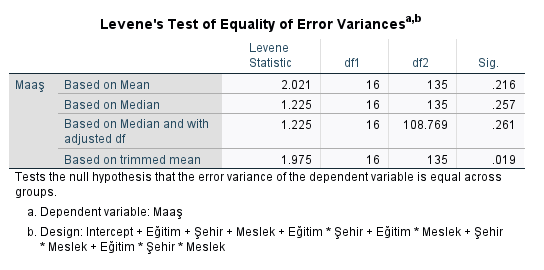
Her şeyden önce, Levene’s Test ile, grupların (eğitim, meslek, şehir) maaşları arasındaki varyansların homojen (yani birbirine benzer dağılıma sahip) olup olmadığına bakmamız gerekiyor. Buna, Levene’s Test tablosundan bakıyoruz.

Aşağıdaki tabloda, “Based on Mean” satırındaki “Sig.” değeri 0.05’ten büyük olmalı. Eğer büyük ise, ANOVA yorumlamaya normal bir şekilde devam edebiliriz. Bu örnekte, 0.216 çıktı yani 0.05’ten büyük. O zaman, ANOVA yapmaya güzelce devam edebiliriz.

Eğer Levene’s Test sonucu p değeri 0.05’ten küçük çıksaydı, ANOVA yapmak yerine, non-parametrik testler olan Kruskal-Wallis, Welch ya da Brown-Forsythe testlerinden bir tanesini yapmamız gerekecekti.

Adım 2: ANOVA p değeri yorumlama

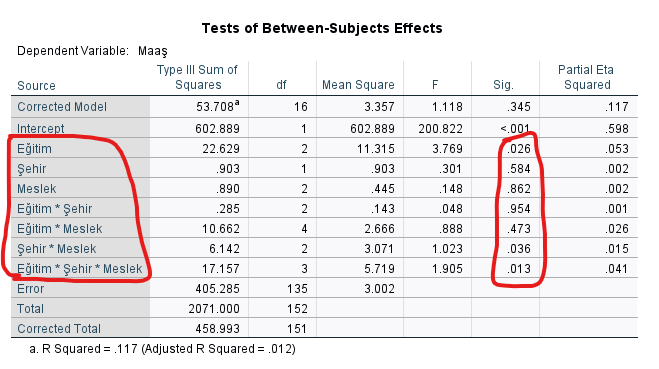
Hangi bağımsız değişkenlerin, bağımlı değişken olan maaş üzerinde etkisi olduğunu görmek için, “Tests of Between-Subjects” tablosuna bakıyoruz. Burada, kırmızı kutu içine alınan yerlerdeki “Sig.” yani p değerlerine bakmak lazım.

Örneğin Eğitim satırına bakarak, eğitimin tek başına ele alındığında maaşı etkilediğini görebiliyoruz, p = 0.026 çıkmış. Hangi eğitim seviyeleri arasında fark olduğunu görmek için post hoc testi sonuçlarına bakmalıyız.

Şehir * Meslek satırına bakarsak, şehir ve mesleğin birlikte etkisi maaşı etkilemiş sonucuna varıyoruz, çünkü p değeri 0.036 çıkmış.

Eğitim Şehir * Meslek satırına bakarsak, eğitim şehir ve mesleğin üçünün birlikte etkisi maaşı etkilemiş sonucuna varıyoruz, çünkü p değeri 0.012 çıkmış.

Bu değişkenlerin içindeki hangi gruplardan oluşan kombinasyonların maaşı etkilediğini görmek içinse, ilgili Pairwise Comparisons tablolarına bakmalıyız.

Faktöriyel ANOVA Post-Hoc Yorumlama

Faktöriyel ANOVA sonuçlarında, 1 adet değişkenin grupları arasında anlamlı bir fark tespit edildiyse, bu farkın hangi gruplar arasında olduğunu belirlemek için post-hoc testlere ihtiyaç duyulur. Post-hoc testler, özellikle gruplar arasındaki spesifik farkları incelemek amacıyla kullanılır ve ANOVA sonuçlarından elde edilen genel anlamlılığı daha ayrıntılı bir şekilde anlamamıza yardımcı olur.

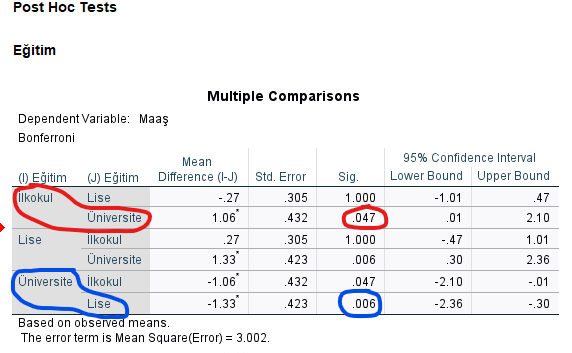
ANOVA testi sonucunda, Eğitim değişkeninin grupları arasında anlamlı bir maaş farkı bulunmuş.

SPSS’in bize verdiği tablolarda, “Post Hoc Tests” başlıklı bölümü buluyoruz ve “Eğitim” başlıklı tabloya bakıyoruz. Burada, kırmızı yuvarlak içinde ilkokul-üniversite arasındaki maaş farkının p değeri 0.047 yani istatistiksel olarak anlamlı bir fark. Aynı zamanda, mavi yuvarlak içinde lise-üniversite arasındaki maaş farkının p değeri de 0.006, bu da istatistiksel olarak anlamlı bir fark.

Not: SPSS tablolarında, eğitimin maaşa tek başına etkisini gösteren, post hoc tablosundan başka, “Pairwise Comparisons” başlıklı bir tablo daha var. Yalnızca tek değişkenin grupları arasındaki farka bakacağımız zaman, bu Pairwise Comparisons tablosuna bakmamamız gerekiyor. Post Hoc testi, tek bağımsız değişkenden oluşan gruplar arasındaki farkı algılamada Pairwise Comparisons tablosuna göre daha güçlüdür ve tercih edilmelidir.

Aşağıdaki tabloya bakmamamız gerekiyor, dikkat.

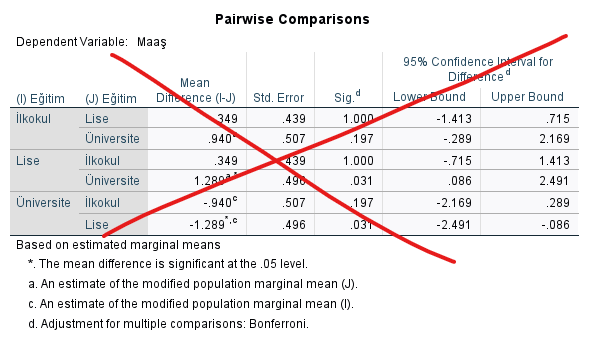
Faktöriyel ANOVA Etkileşim Yorumlama (SME Analysis)

Eğer 2 veya daha fazla bağımsız değişkenin birbirleriyle etkileşimi daha derinlemesine incelenmek isteniyorsa, işte o zaman post hoc yerine başka tablolara bakmak gerekir. Bu şekilde, iki faktörün etkileşiminin gruplar arasında bir fark yaratıp yaratmadığını görmek için ise SME analysis (yani “basit temel etki analizi”) yapmamız gerekiyor.

SME analysis yapmak için, SPSS’te yeniden Analyze -> General Linear Model -> Univariate tuşlarına basıp Univariate penceresinde, “EM Means” butonuna basmamız gerekiyor.

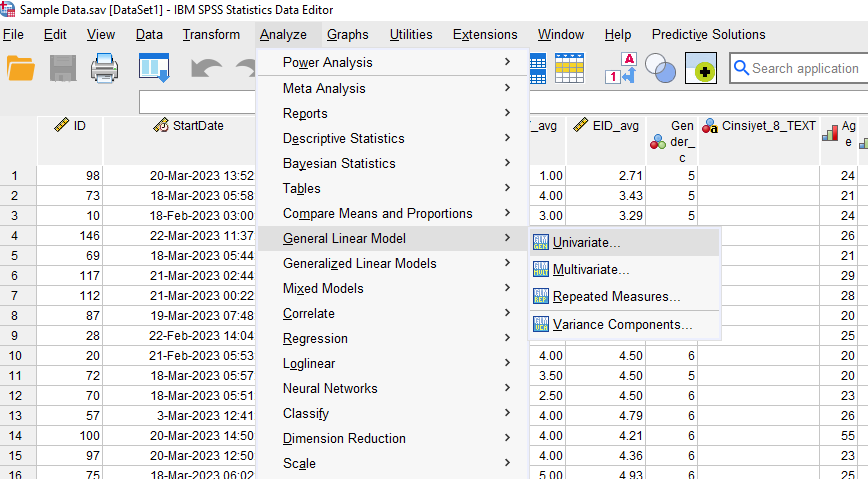
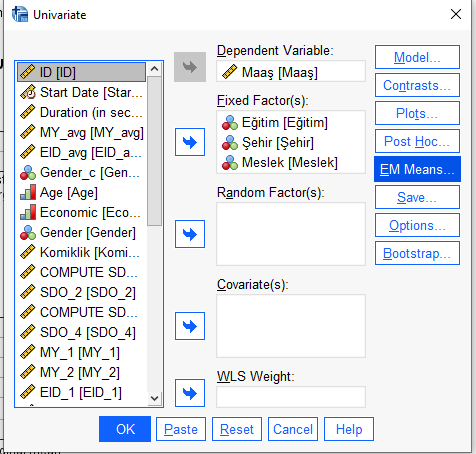
Bizim bu örneğimizde, yukarıda Şehir * Meslek ve Eğitim * Şehir * Meslek değişkenlerinin grupları arasında anlamlı bir fark bulunmuştu. Bu yüzden açılan pencerede, Şehir * Meslek ve Eğitim * Şehir * Meslek etkileşimlerini, sol kutudan alıp sağ kutuya şekildeki gibi taşımak gerekiyor. Sonra “Continue”ya basacağız.

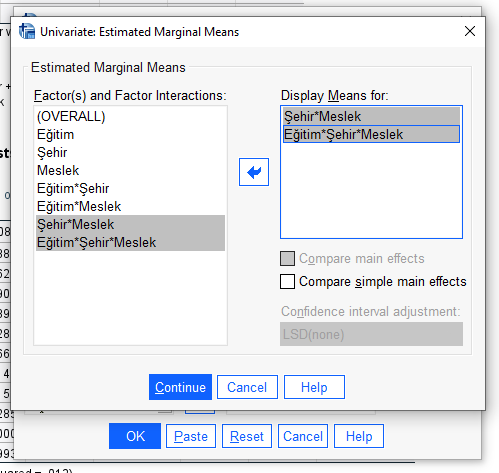
Şimdi, “Univariate” penceresinde, “Paste” butonuna basacağız.

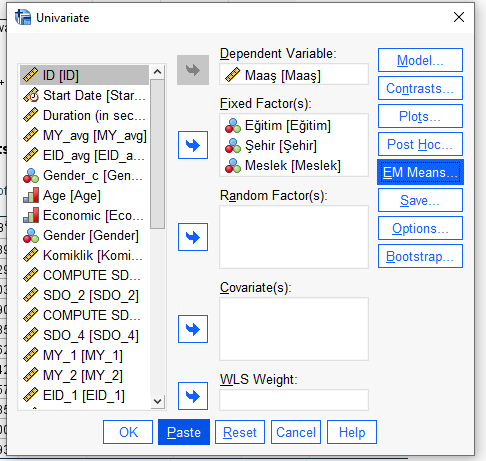
Böyle bir Syntax penceresi açılacak. İçinde kod olması sizi korkutmasın, çok kolay işlemler yapacağız.

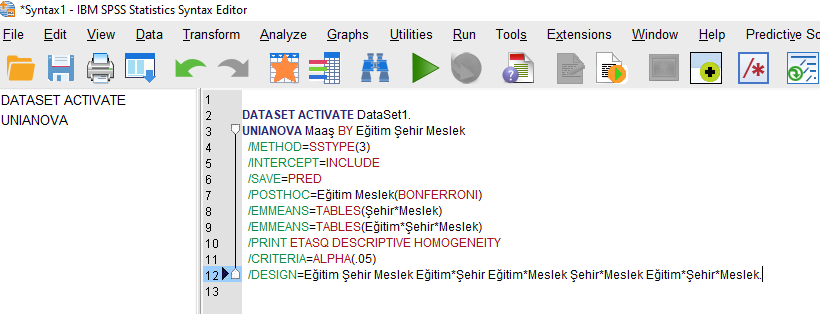
Bu Syntax dosyasında, küçük değişiklikler yapacağız. /EMMEANS ile başlayan 8. ve 9. numaralı satırdaki yazıyı siliyoruz ve onun yerine şu satırları ekliyoruz:

/EMMEANS = TABLES (Şehir * Meslek) compare (Şehir) ADJ (BONFERRONI)

/EMMEANS = TABLES (Şehir * Meslek) compare (Meslek) ADJ (BONFERRONI)

/EMMEANS = TABLES (Eğitim * Şehir * Meslek) compare (Eğitim) ADJ (BONFERRONI)

/EMMEANS = TABLES (Eğitim * Şehir * Meslek) compare (Şehir) ADJ (BONFERRONI)

/EMMEANS = TABLES (Eğitim * Şehir * Meslek) compare (Meslek) ADJ (BONFERRONI)

Siz kendi bağımsız değişkenlerinizin adı neyse buraya onları yazarsınız.

Yazdıktan sonra, ekran aşağıdaki gibi görünecek. Kırmızı ok ile gösterilen butona basarak analizi başlatıyoruz.

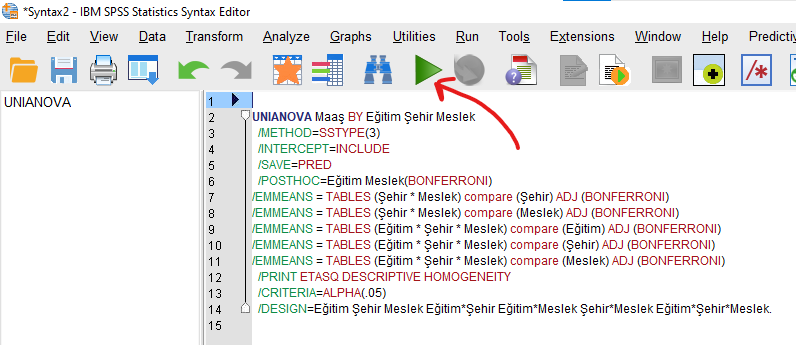
SPSS analizi yapacak ve bize tabloları verecek.

En önemli tablo, “Pairwise Comparisons” tablosudur. Hatırlarsanız, yukarıdaki “Tests of Between-Subjects Effects” tablosunda, şehir ve mesleğin birlikte birlikte değerlendirildiğinde ise maaşa anlamlı etkisi olduğunu bulmuştuk. Aynı zamanda, eğitim şehir ve mesleğin üçü birlikte birlikte değerlendirildiğinde yine maaşa anlamlı etkisi olduğunu bulmuştuk. Aşağıdaki “Pairwise Comparisons” tablolarında bu etkileri daha detaylı inceleyebileceğiz.

Aşağıdaki tabloya göre, katılımcılar önce meslek sonra şehire göre gruplandığı zaman, maaş üzerinde anlamlı hiçbir etki bulunmamış. Bütün “Sig.” yani p değerleri 0.05’ten yüksek.

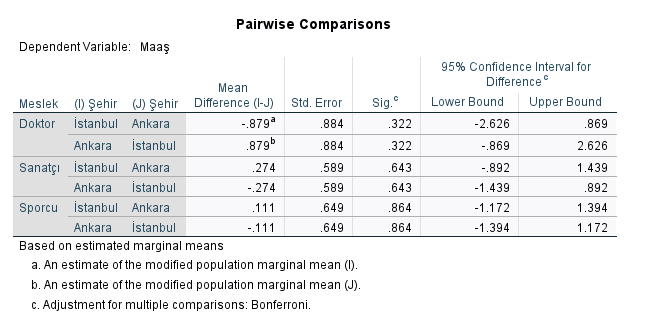
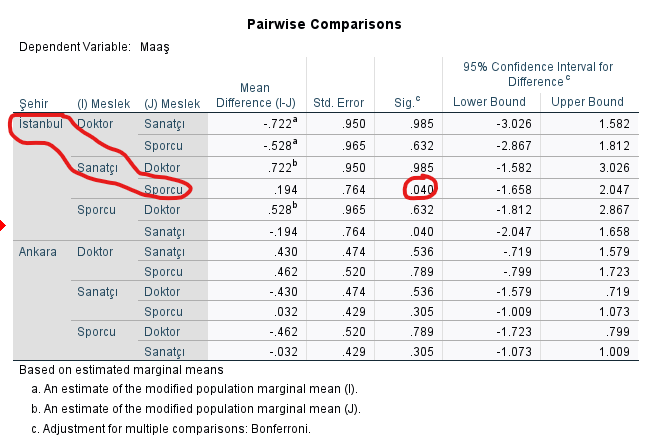
Aşağıdaki tabloya göre, katılımcılar önce şehir sonra mesleğe göre gruplandığı zaman, İstanbul’da yaşayan sanatçıların maaşıyla İstanbul’da yaşayan sporcuların maaşı arasında anlamlı bir fark bulunmuş. Çünkü “Sig.” yani p değeri 0.040 çıkmış, 0.05’ten küçük.

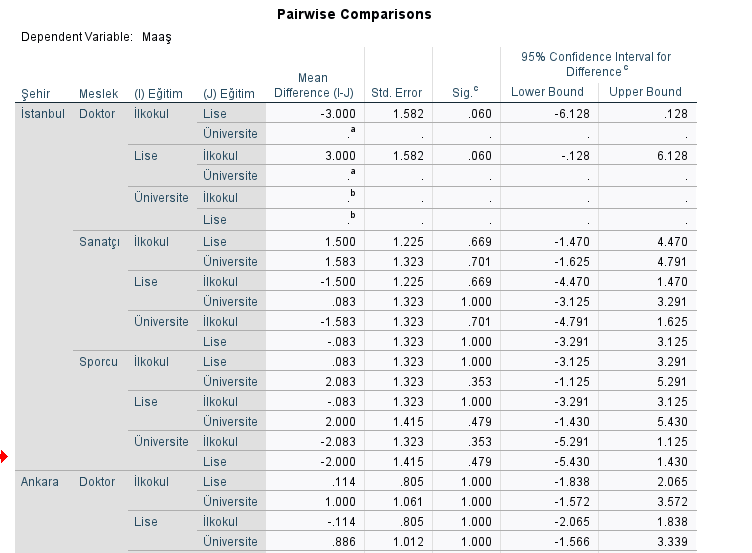
Aşağıdaki tabloya göre, katılımcılar önce şehir sonra meslek sonra eğitime göre gruplandığı zaman, maaş üzerinde anlamlı hiçbir etki bulunmamış. Çünkü bütün “Sig.” yani p değerleri 0.05’ten yüksek.

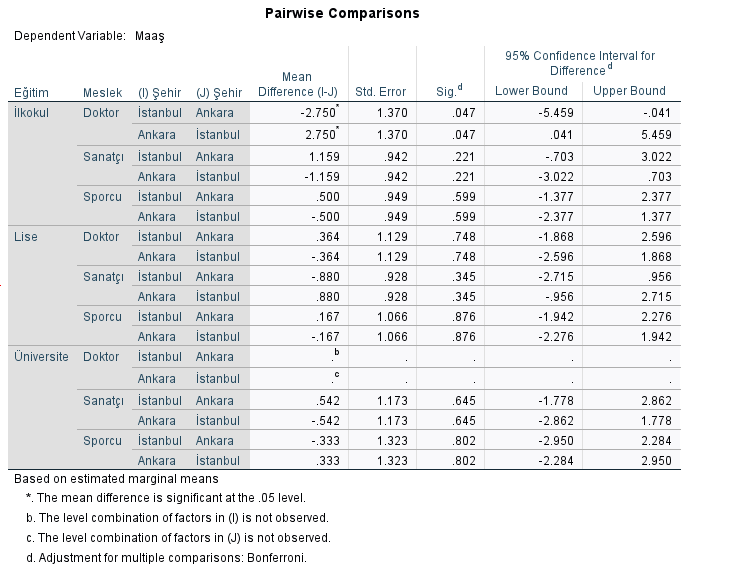
Aşağıdaki tabloya göre, katılımcılar önce eğitim sonra meslek sonra şehire göre gruplandığı zaman, (ilk iki satırda) ilkokul mezunu doktorların maaşları, Ankara’da ve İstanbul’da birbirinden anlamlı şekilde farklı, çünkü “Sig.” yani p değeri 0.047 çıkmış, 0.05’ten küçük.

(Elbette ilkokul mezunu doktor diye bir şey yok fakat bu örnekte başta rastgele değişkenler verdim ve ortaya böyle mantıksız bir şey çıktı, sabahtan beri bu yazı üzerinde uğraşıyorum artık yeni değişken yazıp yeniden başlamak için çok geç)

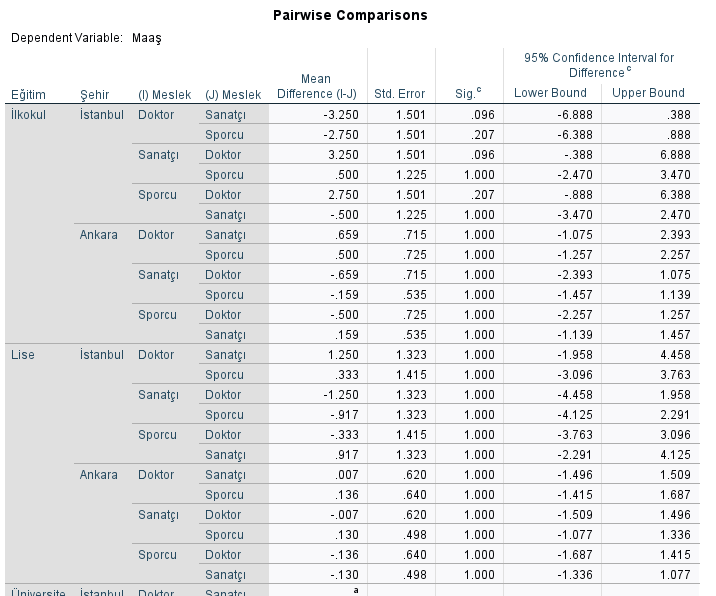
Katılımcılar önce eğitime sonra şehire sonra mesleğe göre gruplandığı zaman, maaş üzerinde anlamlı hiçbir etki bulunmamış. Bütün “Sig.” yani p değerleri 0.05’ten yüksek.

Yani bu testlere bakarak görmüş olduk ki, katılımcılarımızı farklı farklı kombinasyonlarla gruplandırırsak, bağımsız değişkenlerin birbirleriyle spesifik kombinasyonlarda etkileşiminin (eğitim, meslek, şehir) bağımlı değişkeni (maaş) etkileyebileceğini bulabiliyoruz.

Siz kendi araştırmanızdaki grupların hangi kombinasyonlarda etkileşimini merak ediyorsanız buradaki gibi Syntax kullanarak istediğiniz kombinasyondaki etkileşiminin istatistiksel olarak anlamlı olmadığını inceleyebilirsiniz.

Faktöriyel ANOVA Etki Büyüklüğü Yorumlama

Kısmi eta-kare (partial eta-squared), faktöriyel ANOVA analizinizi yaptıktan sonra eğer istatistiksel olarak anlamlı bir sonuç bulmanız durumunda, bulduğunuz sonucun ne kadar büyük bir etki büyüklüğüne sahip olduğunu anlamanız için kullanabileceğiniz bir etki büyüklüğü yorumlama ölçüsüdür.

Etki büyüklüğü değerine, ANOVA sonucu bulduğumuz “Tests of Between-Subjects Effects” tablosundan bakabiliriz. Bu tabloda, etki büyüklüğünü ilgili satırın “Partial Eta Squared” değerinden okumamız gerekiyor.

İstatistiksel olarak anlamlı yani p değeri 0.05’ten küçük olan satırların etki büyüklüğünü bilsek yeterli.

Eğitim’in “Partial Eta Squared” değeri 0.053 çıkmış, yani eğitim, maaştaki değişimi %5.3 oranında etkiliyor diyebiliriz.

Şehir * Meslek etkileşiminin “Partial Eta Squared” değeri 0.015 çıkmış, yani şehir ve meslek birlikte ele alındıklarında, maaştaki değişimi %1.5 oranında etkiliyor diyebiliriz.

Eğitim * Şehir * Meslek etkileşiminin “Partial Eta Squared” değeri 0.041 çıkmış, yani eğitim şehir ve meslek birlikte ele alındıklarında, maaştaki değişimi %4.1 oranında etkiliyor diyebiliriz.

Faktöriyel ANOVA hakkında her şey bu kadardı. İlk olarak ANOVA analizimizi yaptık, daha sonra post hoc testleri ile hangi grupların maaşları arasında fark olduğuna ve SME analysis ile grupların etkileşiminin maaşa nasıl etki ettiğine baktık. Son olarak da, bulduğumuz istatistiksel olarak anlamlı sonuçların ne kadarlık bir etki büyüklüğüne işaret ettiğini inceledik. Artık, faktöriyel ANOVA analizimizi raporlama aşamasına geçebiliriz.

Faktöriyel ANOVA Sonucu Raporlama (APA)

Aşağıda, örnek bir faktöriyel ANOVA raporu görebilirsiniz. Bu rapordaki değişkenleri ve sayıları kendi deneyinize uydurarak aynı formatta bir ANOVA raporu yazabilirsiniz.

İlk olarak, şehir eğitim ve meslek değişkenlerinin maaş üzerindeki etkilerini değerlendirmek amacıyla faktöriyel ANOVA analizi gerçekleştirildi. Bulgularımıza göre, eğitim faktörü açısından istatistiksel olarak anlamlı bir fark tespit edildi (F(2, 135) = 3.769, p = .026). Post hoc testleri uyguladığımızda, üniversite mezunlarının hem ilkokul, hem de lise mezunlarından daha yüksek maaş aldığını gözlemledik (p = .047, p = .006).

Daha sonra, eğitim şehir ve meslek faktörlerinin birlikte değerlendirildiği SME analizi gerçekleştirildi. Bu analizde, ilkokul mezunu doktorların maaşları, Ankara’da ve İstanbul’da birbirinden anlamlı şekilde farklı (p = .047) olarak bulundu.

Son olarak, elde edilen istatistiksel anlamlılıkların etki büyüklüğünü değerlendirdik. Maaş üzerinde eğitimin tek başına anlamlı etkisi %5.3 iken, şehir ve meslek etkileşiminin anlamlı etkisi %1.5, üç değişkenin hep birlikte etkileşimi ise %4.1 oranında anlamlı etkiye sahip sonucuna vardık.