SPSS ile Normallik Testi (Normal Dağılım Testi)

Bu yazımızda, “normal dağılım”ın ne demek olduğunu kısaca açıklayıp, bir değişkenin normal dağılım gösterip göstermediğini SPSS progamını kullanarak nasıl anlayabileceğimize bakacağız. SPSS ile normal dağılım test etmek için 3 farklı yöntem kullanacağız. Bu yöntemlerin hepsini birlikte göz önünde bulundurarak, bir değişkenin normal dağılım gösterip göstermediğine artık güvenle karar verebileceksiniz. SPSS ile normal dağılım testi hakkında ihtiyacınız olan bütün bilgileri bu sayfada bulacağınıza eminim.

Normal Dağılım Nedir?

Normal dağılım, istatistikte sıkça kullanılan bir olasılık dağılımı türüdür. Normal dağılım, belirli bir değişkenin değerlerinin belirli bir şekilde dağıldığı bir olasılık dağılımını ifade eder. Bir örnek vermek gerekirse, zeka testi skorları gibi bir değişkeni ele alalım.

Zeka testi skorları normal dağılıma yakın bir dağılım gösterir. Bu, zeka testi skorlarının çoğunlukla ortalamaya yakın değerlerde bulunduğu ve düşük veya yüksek skorların daha az sıklıkla görüldüğü anlamına gelir.

Aşağıda, zeka testi skorlarının normal dağılımını ifade eden bir grafik göreceksiniz:

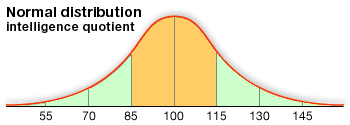
Normal Dağılım Özellikleri Nelerdir?

Normal dağılımın temel özellikleri şunlardır:

1. Ortalama: Zeka testi skorlarının ortalaması belirli bir değere yakın olur. Örneğin, ortalama zeka testi skoru 100 olabilir.
2. Simetri: Normal dağılım, eğri şeklinde simetrik bir dağılıma sahiptir. Ortalamaya yakın skorlar, eğrinin en yüksek olduğu yerdedir ve düşük veya yüksek skorlar eğrinin her iki tarafında daha az sıklıkla bulunur.
3. Çarpıklık ve Basıklık Olmaması: Normal dağılım, çarpıklık (skewness) veya basıklık (kurtosis) gibi aykırı özelliklere sahip değildir. Yani dağılımın ortasında ve uçlarında aşırı değerler nadiren görülür.

Bu normal dağılım özellikleri psikoloji, sosyal bilimler ve doğa bilimleri gibi birçok alanda birçok değişken için geçerli olabilir. Örneğin, bir araştırma, bir grup öğrencinin zeka testi skorlarını incelediğinde, bu skorların normal dağılıma sahip olması, istatistiksel analizlerin daha güvenilir ve etkili bir şekilde yapılabilmesine olanak tanır.

Normal Dağılım Neden Önemlidir?

Korelasyon, regresyon, ANOVA, t testi gibi testler parametrik testlerdir. SPSS programında bu testleri yapıp güvenilir bir sonuca ulaşmak istiyorsak öncelikle test edeceğimiz değişkenlerin skorlarının dağılımının normal dağılım gösterdiğinden emin olmamız gerekiyor. Eğer analiz edeceğimiz değişkenler arasında normal dağılım göstermeyen en az bir değişken varsa yolumuza farklı testlerle devam etmemiz gerekecektir.

SPSS ile Normal Dağılım Test Etme Yöntemleri

Bir değişkenin değerlerinin normal dağılıma sahip olup olmadığını anlamanın çeşitli yolları vardır. Tek bir yolla anlamak yerine, farklı farklı yöntemlerle normal dağılımın olup olmadığına bakmak ve varılan sonuçları birlikte değerlendirmek en sağlıklı şekilde karar vermemizi sağlar.

SPSS ile yapılan analizlerde, 3 temel yöntemle normal dağılım varlığı test edilir. Bunlar şu şekilde listelenebilir:

1. Kolmogorov-Smirnov veya Shapiro-Wilk gibi normallik testleri uygulayıp p değerlerine bakmak
2. Çarplıklık & Basıklık (Skewness & Kurtosis) değerlerine bakmak
3. Gözümüz ile dağılımın grafiğine bakmak

1) SPSS Normallik Testi ile Normal Dağılım Testi

SPSS’te bir normallik testi kullanarak test edeceğimiz değişkenlerin normal dağılım gösterip göstermediğini öğrenmek için, SPSS’te aşağıdaki adımları izlememiz gerekiyor.

Adım 1:

İlk önce SPSS’te Analyze -> Descriptive Statistics -> Explore butonlarına basıyoruz.

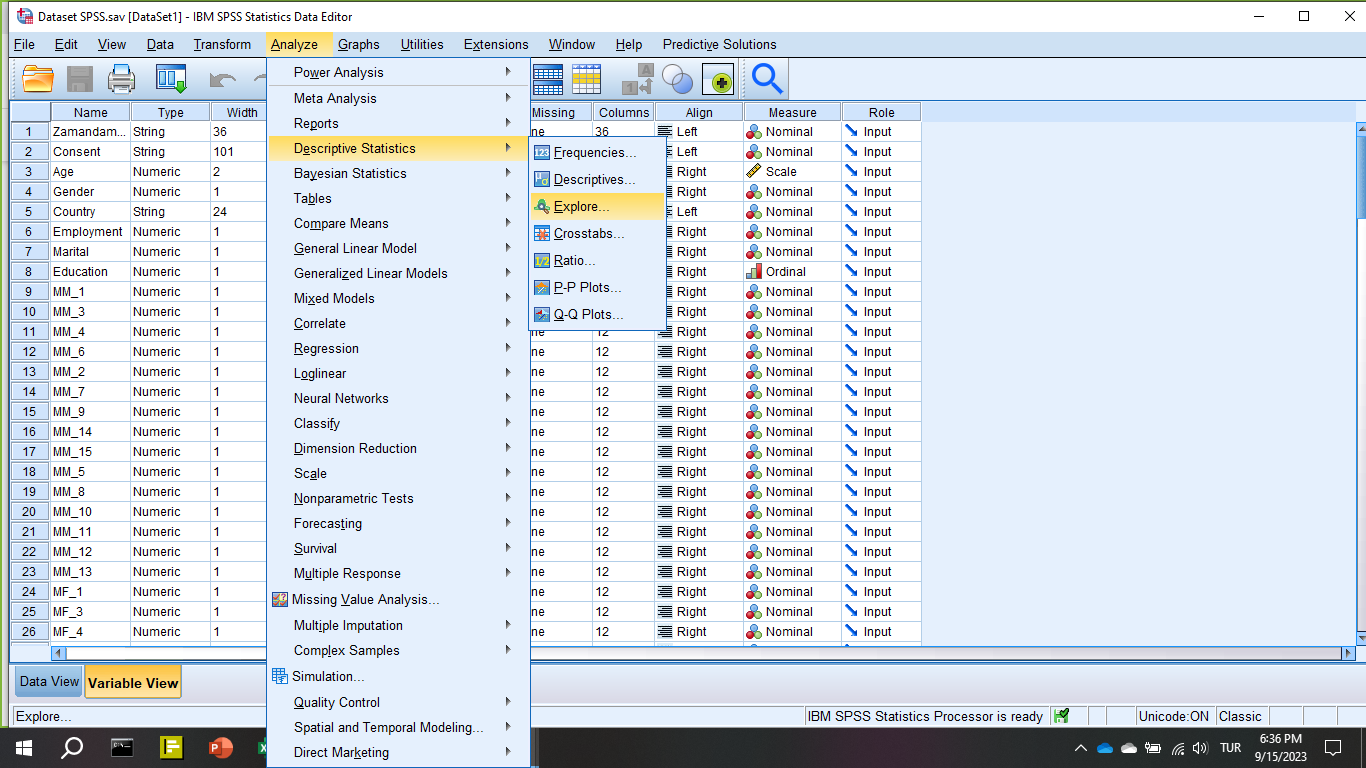
Adım 2:

Açılacak olan yeni pencerede, test etmek istediğimiz bütün değişkenleri (1 ya da birden fazla olabilir) sol taraftaki kısımdan alıp sağ taraftaki Dependent List bölümüne koyuyoruz. Sonra Plots butonuna basıyoruz.

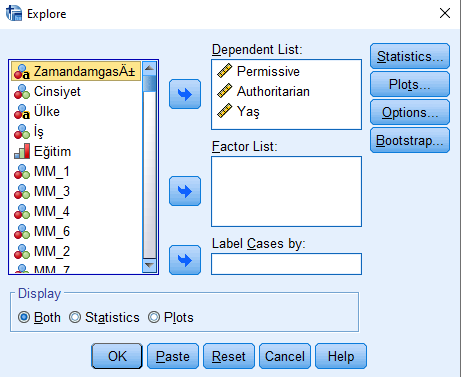
Adım 3:

Aşağıdaki resimde görüldüğü gibi, “Histogram” ve “Normality plots with tests” seçeneklerini işaretliyoruz. Continue’ya basıyoruz. Sonra OK tuşuna basıyoruz.

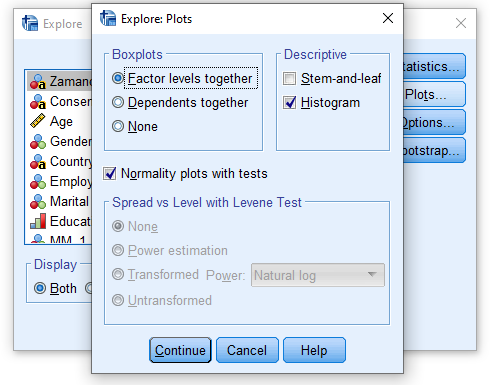
Adım 4:

SPSS, bize yeni bir sayfada sonuçları gösterecektir. Sonuçların gösterildiği sayfada Tests Of Normality tablosuna bakmamız gerekiyor. Kolmogorov-Smirnov veya Shapiro-Wilk’ten bir tanesini seçip, Sig. (significance=anlamlılık yani p değeri) değerine bakmamız gerekiyor. Her satır için ayrı ayrı bakmamız gerekiyor. Eğer bir satırdaki değişkenin Sig. değeri 0.05’ten büyükse o değişken normal dağılıma sahip, 0.05’ten küçükse o değişken normal dağılıma sahip değil sonucunu çıkarabiliriz. Kolmogorov-Smirnov veya Shapiro-Wilk’ten hangisini seçmemiz gerektiği hakkında emin değilseniz, cevabı aşağıda, resmin altında bulabilirsiniz.

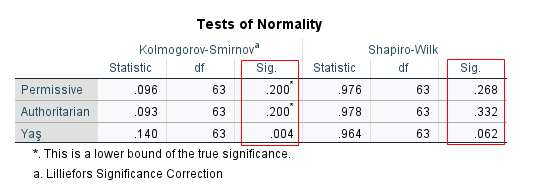
Kolmogorov-Smirnov Testi vs. Shapiro-Wilk Testi

Normallik analizi yaptığımızda, SPSS bize 2 tane farklı normallik testi sonucu gösteriyor. Testlerin birinin adı Kolmogorov-Smirnov ve diğerinin adı Shapiro-Wilk testi. Bunların arasından birini seçip, tabloda onun olduğu bölümü okumamız gerekiyor. Hangi normallik testini seçmek gerektiği konusunda kesin kurallar yok. Bazı okullarda, katılımcı sayısı 50 kişinin üstünde olduğu zaman Kolmogorov-Smirnov testini seçmek gerektiği öğretilirken, bazı okullarda katılımcı sayısı 100 kişinin altında olduğu zaman Shapiro-Wilk testini yapmak gerektiği öğretiliyor. İnternette hangi kaynaktan okuduğunuza göre hangi testi yapmanız gerektiğiniz hakkında farklı tavsiyeler alabiliyorsunuz. Bu da kafa karışıklığına sebep olabiliyor.

Kolmogorov-Smirnov Testi mi yoksa Shapiro-Wilk Testi mi seçmeliyim?

Dünya çapında birçok üniversitede okutulan Andy Field’ın istatistik kitabında, her durumda Shapiro-Wilk testini tercih etmek gerektiği yazıyor. Kitapta yazanlara göre, Kolmogorov-Smirnov testi, 0.05’in altında değerler vermeye daha çok yatkın. Bu da, aslında normal dağılıma yakın dağılım gösteren değişkenlerin normal dağılıma sahip değilmiş gibi görünmesine yol açıyor. Bu hatanın önüne geçmek için Shapiro-Wilk testini yapmanın daha mantıklı bir yol olduğu yazıyor.

Yukarıdaki resimdeki tablonun üçüncü satırında da görebileceğiniz üzere, bu verideki Yaş değişkeninin Sig. (yani p) değeri Kolmogorov-Smirnov testine göre 0.004 iken, Shapiro-Wilk testine göre 0.062 olarak bulunmuş. Yani, Yaş değişkenini Kolmogorov-Smirnov testine göre normal olarak kabul edemiyorken, Shapiro-Wilk testine göre normal olarak kabul edebiliyoruz. Bu örnekte, Andy Field’ın tavsiyesine uyup, Kolmogorov-Smirnov testi yerine Shapiro-Wilk testine bakarsak, Yaş değişkeni normal dağılım gösteriyor şeklinde bir sonuca ulaşabiliriz.

Not: Eğer hocanız Shapiro-Wilk yerine Kolmogorov-Smirnov testini tercih etmeniz gerektiği konusunda ısrar ediyorsa, hocanızın suyuna gitmek daha mantıklı bir seçim olacaktır.

2) SPSS Çarpıklık & Basıklık Değeri ile Normal Dağılım Testi

Çarpıklık ve basıklık, bir dağılımın normal dağılımdan ne kadar uzaklaşmış olduğunu gösteren iki ölçüm değeridir. Önce çarpıklık ve basıklık terimlerinin ne anlama geldiğini açıklayıp sonra bu değerlere bakarak normal dağılım olup olmadığına nasıl karar veririz ona bakalım.

UYARI: Çarpıklık – Basıklık değerine bakarak normal dağılıma karar vermek, birkaç yüz kişiye kadar olan büyüklükte örneklemler için geçerli bir yöntemdir. Birkaç yüzden fazla kişiden oluşan çok büyük örneklemlerde, normal dağılıma karar vermek için çarpıklık – basıklık değerlerine bakılması uygun değildir. Diğer yöntemler tercih edilmelidir.

Çarpıklık Nedir

Çarpıklık, bir veri setinin ortalama değerinin grafiğin sağına ya da soluna ne kadar kaydığını gösterir. Aşağıdaki resimde inceleyebilirsiniz.

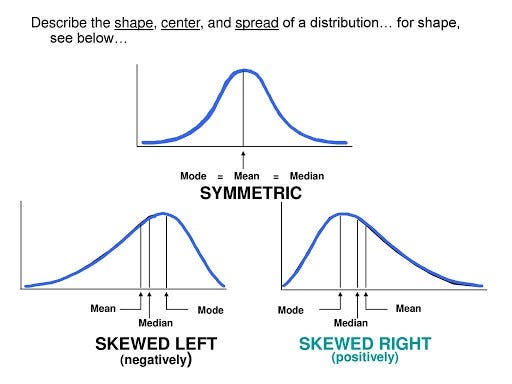
Basıklık Nedir

Basıklık, bir veri setinin ortalama değerine sahip değerlerin veri setinde ne kadar yoğun olarak geçtiğini gösterir. Aşağıdaki resimde inceleyebilirsiniz.

SPSS’te Çarpıklık & Basıklık Değerine Göre Normal Dağılıma Karar Vermek

SPSS bize yukarıdaki gibi normallik testi tablolarından başka, çarpıklık & basıklık değerlerinin olduğu “Descriptives” başlıklı bir tablo daha verecek. Bu tabloda, kırmızı yuvarlak içine aldığım skewness ve kurtosis satırları, çarpıklık ve basıklık değerlerini verir.

Çok da istatistiksel olarak tutarlı olmayan bir kısa yol olarak, bu SPSS tablolarındaki çarpıklık ve basıklık değerleri eğer -1 ile +1 arasında ise, normal dağılım vardır demeyi tercih edebiliriz.

İstatistiksel olarak daha tutarlı ama daha ileri bir seviye yöntemi, tabloların altında “z-skoru” başlığı ile açıklıyorum.

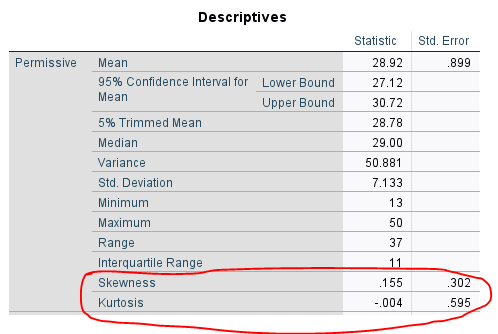
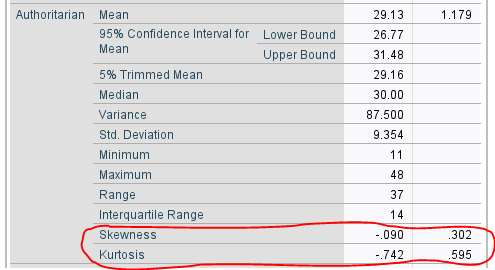
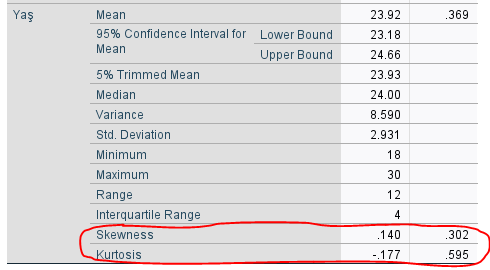
Yukarıdaki tablolara göre, bütün değişkenlerin skewness – kurtosis skorları -1 ile +1 arasında. Yani çarpıklık – basıklık değerlerine kısa yoldan bakarak normal dağılım var mı diye karar verecek olursak, normal dağılım var diyebiliriz.

Normallik Testi ve Çarpıklık & Basıklık Değeri Karşılaştırma

Şimdi aşağıdaki tabloya bakalım. Deminki Kolmogorov-Smirnov ve Shapiro-Wilk testlerindeki p değerlerini hatırlayacak olursak, Permissive ve Authoritarian değişkenlerinin p değerlerinin bu testlerde de 0.05’in üstünde çıktığını yani normal dağılım var yönünde bir sinyal verdiğini görebiliriz. Yeni bulduğumuz Çarpıklık – Basıklık değerleri de bununla tutarlıdır.

Fakat Yaş değişkenine bakacak olursak, normallik testlerindeki p değerlerinin bir tanesi 0.05’ten küçük, bir tanesi de 0.05’ten çok az büyüktür. Bu belirsizliğe sebep olmaktadır. İşte burada ek olarak Çarpıklık – Basıklık değerine de bakmak, normallik konusunda karar vermemize yardımcı oluyor. Yaş değişkeninin Çarpıklık – Basıklık değeri, -1 ile +1 arasında olduğu için, “Yaş değişkeni normal dağılıma sahiptir” şeklinde bir yorumlama yapabilmekteyiz.

Çarpıklık & Basıklık Z-Skoru’na Göre Normal Dağılım Hesaplamak

Ghasemi & Zahediasl’ın 2012’de yayınladıkları makale, çarpıklık ve basıklık değerlerine göre normal dağılım var olup olmadığına karar verme konusunda daha yüksek kalite standartları belirlemiştir. Bu alt başlıkta bu yöntemi açıklayacağım. Makalenin referansını sayfanın en altında Referanslar bölümüne ekledim, bakabilirsiniz.

Bu makaleye göre, normal dağılıma karar verirken çarpıklık ve basıklık değerlerini yorumlamak için, bunları standardize etmek gerekmektedir. Yani z-skoru denen standart skor türüne dönüştürülmelidir. Bu oldukça basittir. Aşağıdaki formül ile çarpıklık (skewness) ve basıklık (kurtosis) değerleri z-skoruna dönüştürülebilir.

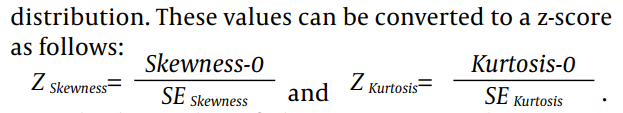
Bu formül şu anlama gelmektedir: Çarpıklık değerinin, Çarpıklık Standart Hata değerine bölümü, “çarpıklık z-skoru”nu verir. Basıklık değerinin, Basıklık Standart Hata değerine bölümü, “basıklık z-skoru”nu verir.

Pratik olacak olursak: Yukarıdaki SPSS tablosunda soldaki sütun Statistic, sağdaki sütun da Standard Error değerini gösteriyor.

Yani skewness satırında soldaki değeri sağdaki değere bölersek, çarpıklık (skewness) değerine ait z-skorunu bulmuş olacağız.

Aynı şekilde kurtosis satırında soldaki değeri sağdaki değere bölersek, basıklık (kurtosis) değerine ait z-skorunu bulmuş olacağız.

Çarpıklık & Basıklık Z-Skoru Değerleri Ne Anlama Geliyor?

Pratik olarak, eğer bulduğumuz Çarpıklık ve Basıklık z-skoru değerleri, +1.96’dan küçük veya -1.96’dan büyük ise, güvenle normal dağılım var diyebiliriz.

Ghasemi & Zahediasl’ın (2012) makalesine göre, Çarpıklık & Basıklık z-skoru değeri, eğer ±1.96’dan büyük ise, p<0.05 istatistiksel anlamlılık seviyesinde “normal dağılım yok” diyebiliriz. Daha küçük z-skoru değeri var ise “normal dağılım var” diyebiliriz. Küçük örneklem büyüklüklerinde normal dağılım var mı diye bakarken bu değerlere bakarak güvenle yorum yapabiliriz.

Eğer Çarpıklık & Basıklık z-skoru değeri, ±2.58’den büyük ise, p<0.01 istatistiksel anlamlılık seviyesinde “normal dağılım yok” diyebiliriz. Daha küçük z-skoru değeri var ise “normal dağılım var” diyebiliriz. 200’den büyük bir örneklem büyüklüğüne sahipsek normal dağılım var mı diye bakarken bu yöntemi kullanabiliriz.

Eğer Çarpıklık & Basıklık z-skoru değeri, ±3.29’dan büyük ise, p<0.001 istatistiksel anlamlılık seviyesinde “normal dağılım yok” diyebiliriz. Bu eşik değerini kullanmak pek tavsiye edilmemektedir, ±2.58’den büyük z-skoru değerleri normal dağılımdan çok fazla uzaklaşmış kabul edilir.

3) SPSS Grafiğe Gözümüz ile Bakarak Normal Dağılım Testi

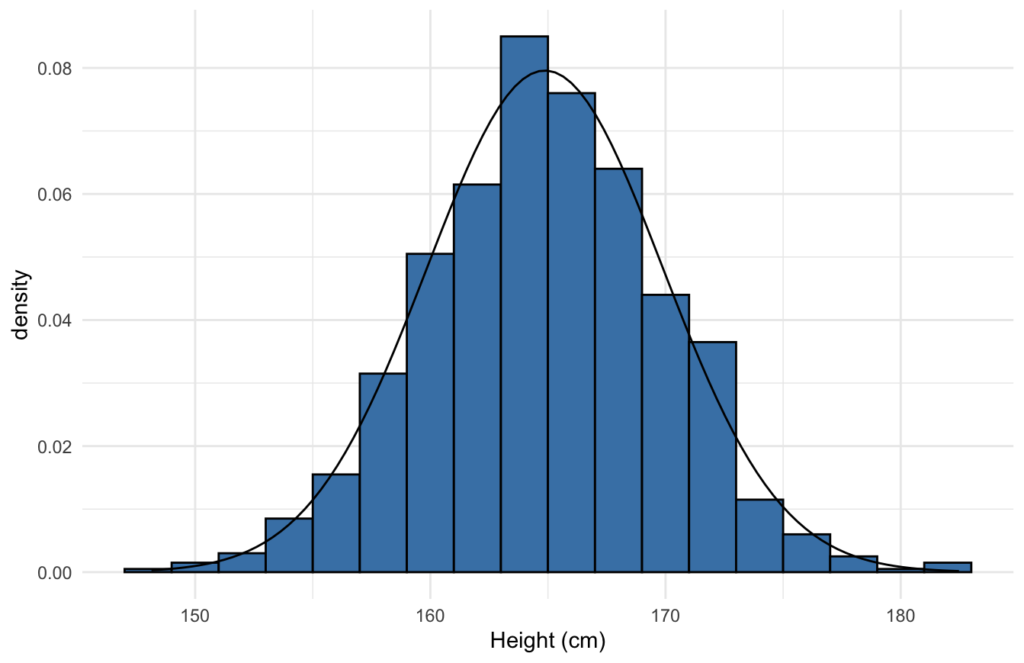
Andy Field’ın tavsiyelerinden biri de normal dağılıma karar verirken grafiklere bakmaktır. Sadece Shapiro-Wilk testi veya Kolmogorov-Smirnov testi sonucuna ve skewness-kurtosis değerlerine değil, gerçek grafiğe de gözümüzle bakıp normal dağılım sayıp sayamayacağımızı belirlemeliyiz. Normal dağılım gösteren bir grafik aşağıdaki gibi görünür:

Bu sayfada yaptığımız örnekte SPSS’in bize verdiği sonuçlar arasında grafikler de bulunuyor. SPSS sonuç sayfamızda, tablolarla beraber aşağıdaki gibi grafikler de görebiliriz. Burada Yaş değişkenine ait Histogram grafiğini bulmamız gerekiyor. Grafiğe bakacak olursak, bu değişkenin dağılım şeklinin birebir normal dağılım olmasa da, normal dağılıma yakın bir dağılım olduğunu görebiliriz.

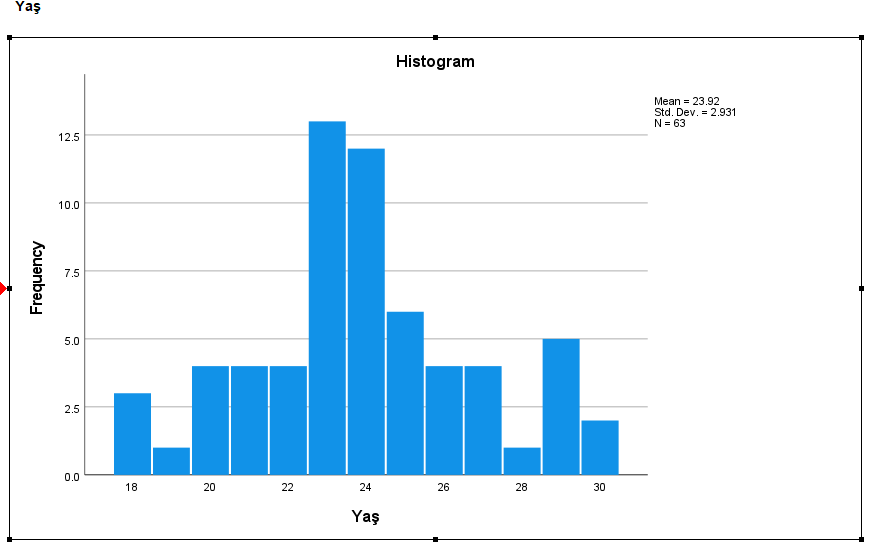
Bu değişkenin Kolmogorov-Smirnov testine göre normal dağılım görünmediğini ama Shapiro-Wilk testine göre normal dağılım göründüğünü biliyoruz. Grafiğin de normal dağılıma yakın bir dağılım olmasından destek alarak, Yaş değişkeninin normal dağılım gösterdiğini güvenle söyleyebiliriz.

Sonuç

Sonuç olarak, incelediğimiz değişkenimizin normal dağılıma sahip olup olmadığını 3 farklı yoldan SPSS ile normallik testleri uygulayarak kontrol ettik. Önce Kolmogorov-Smirnov veya Shapiro-Wilk normallik testleriyle, sonra çarpıklık ve basıklık değerlerini kontrol ederek, sonra da grafiği gözümüzle inceleyerek, değişkenlerimizin üçünün de normal dağılıma sahip olduğu sonucuna vardık.

Kaynak:

Bu sayfadaki yazıları yazarken Andy Field’ın istatistik kitabını ve başka çok sık atıfta bulunulan başka bir makaleyi kullandım. Siz de analizinizi yaptıktan sonra referans olarak bu kitabı ve makaleyi gösterebilirsiniz. Kaynakların APA stili referansı şu şekilde:

Field, A. (2018). Discovering statistics using IBM SPSS statistics: North American edition. SAGE.

Ghasemi, A., & Zahediasl, S. (2012). Normality Tests for Statistical Analysis: A Guide for Non-Statisticians. International Journal of Endocrinology and Metabolism, 10(2), 486–489. doi:10.5812/ijem.3505