SPSS ile Basit Doğrusal (Lineer) Regresyon — Resimli

Basit doğrusal (lineer) regresyon, istatistiksel analizlerde sıkça kullanılan bir tahmin yöntemidir. Bu yöntem, iki devamlı veri tipindeki değişken arasındaki ilişkiyi incelemek ve bir değişkenin aldığı değere bakarak diğer değişkenin alabileceği değeri tahmin etmek amacıyla kullanılır. Bu blog yazısında, basit doğrusal regresyonun ne olduğunu ve SPSS ile nasıl yapıldığını detaylı bir şekilde göreceksiniz.

DOĞRUDAN Regresyon Analizi Adımlarına Geçmek İçin TIKLAYIN

Basit Doğrusal (Lineer) Regresyon Nedir?

Basit doğrusal yani lineer regresyon, istatistiksel bir analiz yöntemidir ve bir bağımlı değişken ile bir veya daha fazla bağımsız değişken arasındaki ilişkiyi incelemek için kullanılır. Bu regresyon yöntemi, bağımlı değişkenin, bir veya daha fazla bağımsız değişkene bağlı olduğunu ve bu ilişkinin doğrusal olduğunu varsayar. Yani, bağımlı değişkenin değeri, bağımsız değişkenlerin değerlerine göre doğrusal olarak tahmin edilebilir.

Doğrusal regresyon analizi yapılabilmesi için, değişkenlerin ikisinin de devamlı (sürekli) veri tipinde olması gerekmektedir.

Basit doğrusal regresyon, y = mx + c formülüyle ifade edilir, burada y bağımlı değişkeni, x bağımsız değişkeni, m eğimi ve c ise kesme noktasıdır. Bu formül, doğrusal bir ilişkinin var olduğunu varsayar ve eğim (m) ve kesme noktası (c) parametrelerini bulmak için kullanılır.

Basit doğrusal regresyon, istatistiksel analizde ve tahmin yapma süreçlerinde yaygın olarak kullanılır. Örneğin, bir pazarlama uzmanı, bir ürün için yapılan reklam harcamaları ve ürünün satış miktarı arasındaki ilişkiyi anlamak için basit doğrusal regresyonu kullanabilir. Bu analiz sayesinde, reklam harcamalarını artırmak veya azaltmak için doğru stratejiler belirlenebilir.

Basit Doğrusal Regresyon Varsayımları

Basit doğrusal regresyon analizi yapabilmemiz için iki değişkenimizin de sürekli veri tipinde olması şarttır. Bunun dışında SPSS ile test edilmesi gereken iki önemli varsayım vardır.

1. Doğrusallık Varsayımı: Model, bağımlı değişken ile bağımsız değişken arasındaki ilişkinin doğrusal olduğunu varsayar. Bu, regresyon çizgisinin bir doğru olduğu anlamına gelir. Eğer ilişki doğrusal değilse, başka bir regresyon yöntemi kullanmanız gerekebilir.
2. Normallik Varsayımı: Basit doğrusal regresyonda, normal dağılım varsayımı, Residual’ların (artıkların = gözlemlenen değerler ile regresyon çizgisi tarafından tahmin edilen değerler arasındaki farklar) normal dağılıma sahip olma gereksinimini ifade eder. Bu varsayım, genellikle büyük örneklem boyutlarında göz ardı edilebilir. Ancak, küçük örneklem boyutlarında bu varsayımın sağlanması önemlidir.
3. Homoskedastisite Varsayımı: Bu varsayım, regresyon analizinde varyansların bağımsız değişkenlerin büyüklüğüne göre değişkenlik göstermemesi anlamına gelmektedir. Lisans ve yüksek lisans seviyesinde bu varsayım genellikle test edilmez, bu yüzden bu varsayımın nasıl test edileceğini bu sayfada anlatmak yerine ayrı bir sayfada anlatıyorum, merak ederseniz bu linke tıklayarak o sayfayı okuyabilirsiniz.

Bu varsayımlar, basit doğrusal regresyon analizi sonuçlarının güvenilir ve geçerli olmasını sağlamak için önemlidir. Varsayımlara uygunluk test edilmeli ve uygunluk sorunları tespit edilirse, analizin sonuçlarına dikkatli bir şekilde yaklaşılmalı ve alternatif analiz yöntemleri düşünülmelidir.

SPSS ile Basit Doğrusal (Lineer) Regresyon Varsayımları Test Etme

Varsayım 1: Doğrusallık Test Etme

Basit doğrusal regresyon analizi için gerekli olan varsayımlardan biri, iki değişkenin doğrusal ilişkiye sahip olmasıdır. SPSS ile bu varsayım şöyle test edilir:

Graphs -> Scatter/Dot butonlarına basıyoruz.

Simple Scatter seçiyoruz. Define’a basıyoruz.

Bağımsız değişkenimizi soldan alıp X Axis bölümüne, bağımlı değişkenimizi Y Axis bölümüne taşıyoruz. OK butonuna basıyoruz.

SPSS bize bir nokta grafiği verecek. Burada, doğrusallık olup olmadığını anlamak için, grafiğin üzerine çift tıklıyoruz.

Açılan yeni pencerede sağdan beşinci Add Fit Line at Total ikonuna basıyoruz.

Nokta grafiğimizin üzerine aşağıdaki gibi bir doğrusal ilişki çizgisi geliyor. Şimdi bu doğrusal ilişkinin istatistiksel olarak anlamlı bir ilişki olup olmadığını anlamak için regresyon analizi yapacağız.

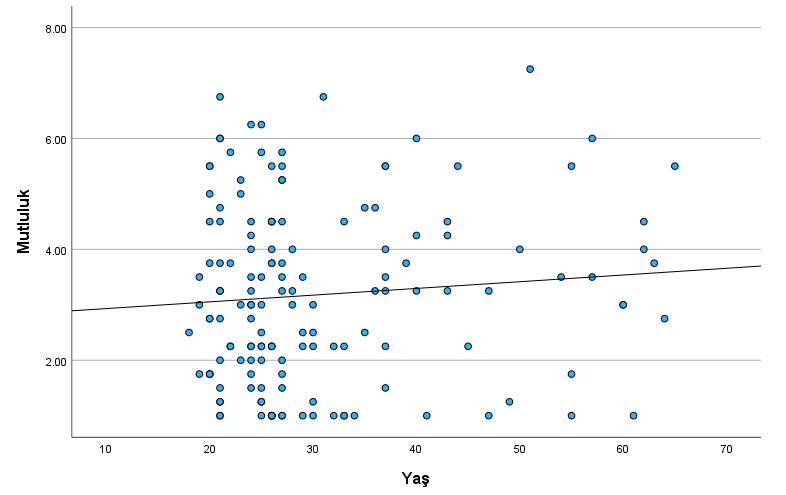
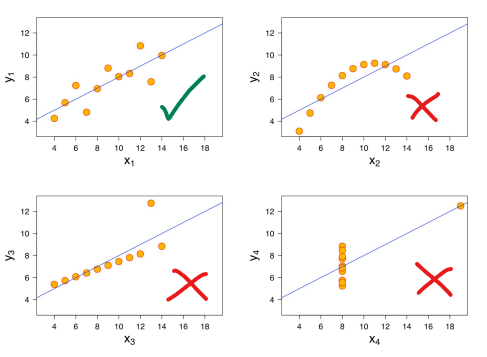
UYARI: Elde ettiğimiz grafik, aşağıdaki resimde kırmızı çarpı işaretli grafiklere benzeseydi, bu, doğrusal ilişki olmadığı anlamına gelirdi. Öyle bir durumda doğrusal regresyon analizi yapamazdık.

Varsayım 2: Normallik Test Etme

Verimizdeki değişkenlerin Residual’larının normal dağılım göstermesi, SPSS’in regresyon analizi sırasında kuracağı regresyon modelinin güvenilir olması için önemlidir. Lineer regresyon için normallik varsayımına SPSS’te şu şekilde bakılır:

Analyze -> Regression -> Linear

Değişkenlerin biri Dependent bölümüne, diğeri Dependent’ın altındaki kutuya konmalı. “Save” butonuna basıyoruz.

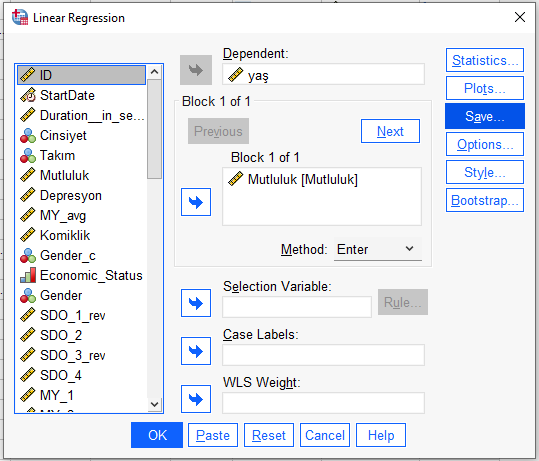
Açılan pencerede Residuals başlığındaki Unstandardized kutucuğunu işaretliyoruz. Aslında Standardized’ı işaretlesek de fark etmez normallik testi analizi sonucu aynı olacak.

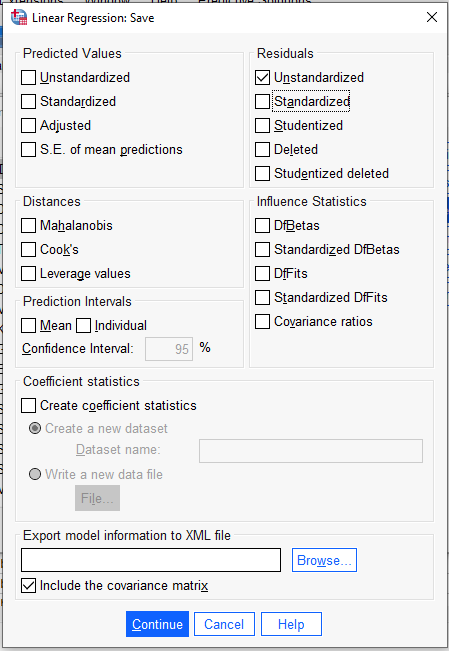
Continue ve OK butonlarına basıyoruz.

Bunu yapınca SPSS bize yeni bir değişken oluşturdu. Bu değişken, verimizdeki her kişi için bir Residual değeri gösteriyor. Bu yeni değişkeni SPSS veri setimizde Variable View’a giderek görebiliriz.

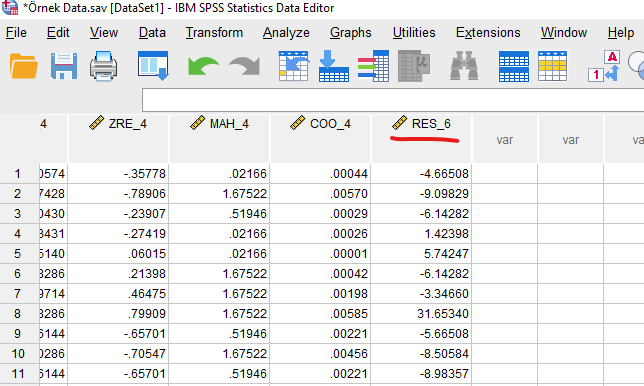
Şimdi bu yeni oluşturduğumuz Residual değerlerinin, normal dağılıma sahip olup olmadığını SPSS ile test edeceğiz.

Analyze -> Descriptive Statistics -> Explore

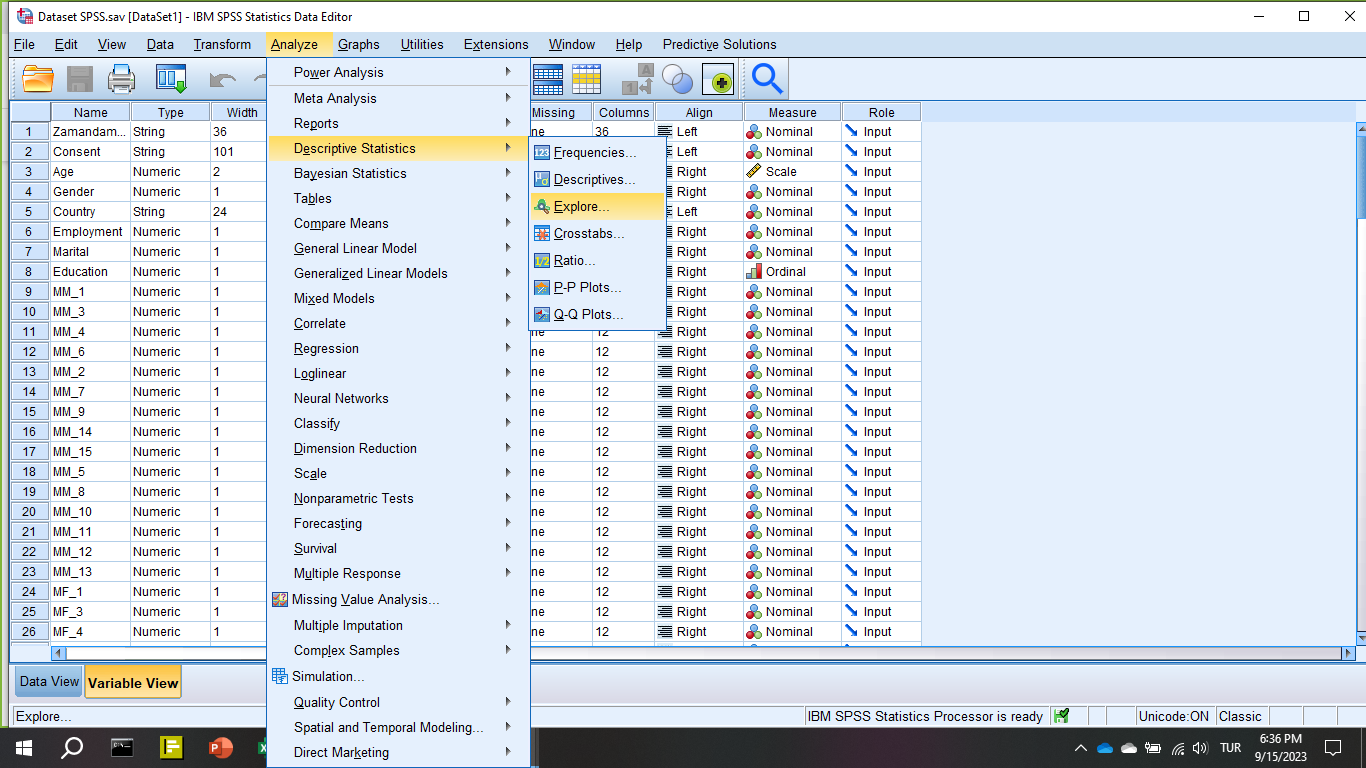
Yeni oluşturduğumuz değişkeni soldaki kutudan bulup Dependent List bölümüne atıyoruz. Sonra “Plots”a basıyoruz.

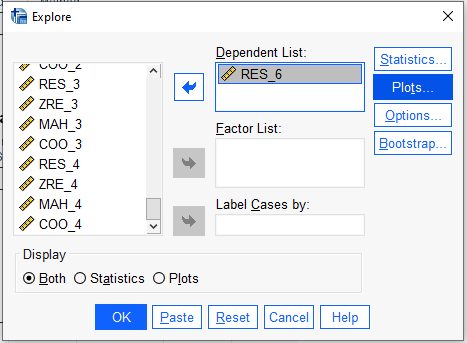
“Histogram” ve “Normality plots with tests” seçeneklerini işaretliyoruz.

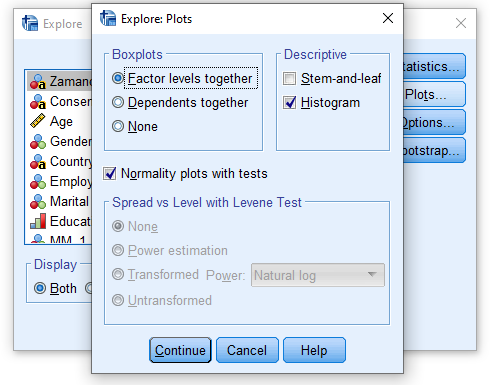
Continue ve OK’a basarsak SPSS bize normallik testi sonucunu verecek.

SPSS’in bize vereceği “Tests of Normality” başlıklı tabloda, “Sig.” değerlerine bakarak normal dağılım olup olmadığına karar verebiliriz. Sig. değeri yani p değeri, 0.05’ten büyük ise, normallik varsayımı sağlanmıştır diyebiliriz. Kolmogorov-Smirnov Sig. değerine mi yoksa Shapiro-Wilk Sig. değerine mi bakmak gerektiği hakkında detaylı yazımı linke tıklayarak okuyabilirsiniz. Shapiro-Wilk seçmek genelde daha güvenilir sonuçlar almamızı sağlar.

Bu örnekte, iki Sig. değeri de 0.05’ten büyük, o yüzden “regresyon analizi yapacağımız değişkenlerin Residual değerleri normal dağılıma sahiptir” diyebiliyoruz.

İki önemli varsayımı da doğruladığımıza göre artık doğrusal regresyon analizimize başlayabiliriz.

SPSS ile Basit Doğrusal (Lineer) Regresyon Nasıl Yapılır?

Aşağıdaki adımları izleyerek SPSS’te kolay bir şekilde lineer regresyon analizi başlatabilirsiniz.

Analyze -> Regression -> Linear

Bağımsız değişkeni “Independent(s)” kutusuna atıp bağımlı değişkeni “Dependent” kutusuna koyuyoruz.

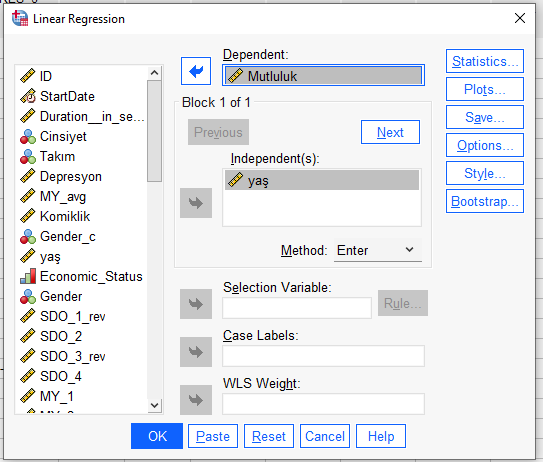
Başka bir işlem yapmamıza gerek yok.

“OK” butonuna basarak analizi başlatıyoruz.

Basit Doğrusal Regresyon SPSS Tablo Yorumlama

Basit doğrusal regresyon analizimizi başlattıktan sonra, SPSS bize bir sürü tablo verecektir. Bu tablolarda nerelere bakmak gerektiğini ve değerleri nasıl yorumlamak gerektiğini aşağıda anlatıyorum.

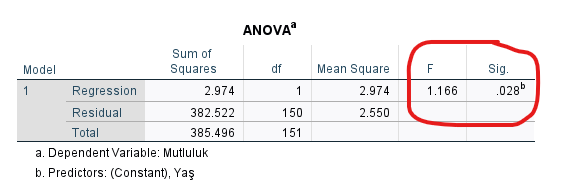
ANOVA tablosundaki “Sig.” değerine bakarak, yaptığımız regresyon analizi sonucunda, iki değişken arasında istatistiksel olarak anlamlı bir ilişki olup olmadığını öğreniyoruz. Eğer 0.05’ten küçük çıkarsa, anlamlı bir ilişki vardır.

Bizim örneğimizde, ANOVA sonucu 0.028 çıktığı için yaş ile mutluluk arasında anlamlı bir lineer ilişki olduğu sonucuna varıyoruz.

Yukarıda hatırlarsanız, basit doğrusal regresyon denklemi y = mx + c olarak ifade ediliyordu. “Coefficients” tablosuna bakarak, analiz ettiğimiz verinin regresyon denklemini kuracağız.

Regresyon denkleminde y bağımlı değişkeni, x bağımsız değişkeni, m eğimi ve c ise sabit değeri ifade ediyor. Bunları şimdi yerlerine yerleştirelim.

(Constant) satırı B sütunu, sabit değeri ifade eder. Yaş satırı B değeri ise eğimi ifade eder. Bu değerler ile kuracağımız regresyon denklemi şöyle oluyor:

Y = 2.810 + (0.012 * X)

Yani, 0 yaşındaki birinin mutluluk değeri (mutluluk ölçeğine göre), 2.810 oluyor. Yaştaki her 1 yaş artış, mutluluk değerinin 0.012 artmasına sebep oluyor.

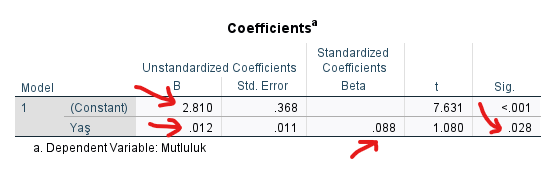
Yine “Coefficients” tablosundaki Beta değeri, regresyon katsayısını ifade eder. Bunu, regresyon analizi raporlama yapılırken raporda p değeriyle birlikte β = 0.088 şeklinde göstermek gerekir.

Basit doğrusal regresyonda, bu Beta değeri aynı zamanda iki değişken arasındaki Pearson’s r korelasyon katsayısını ifade eder. Eğer yaş ile mutluluk arasında bir Pearson korelasyon analizi yaparsak, bulacağımız Pearson’s r korelasyon değeri bu Beta değeri ile aynı olacaktır.

Bu örnekte, yaş ile mutluluk arasında 0.088 (yaklaşık 0.09) büyüklüğünde istatistiksel olarak anlamlı bir korelasyon varmış. Korelasyon büyüklüğü tablosuna bakacak olursak, bu, çok zayıf bir korelasyonu ifade etmektedir.

Dikkat ederseniz “Coefficients” tablosundaki Sig. değeri, “ANOVA” tablosundaki Sig. değeri ile aynı değere sahip.

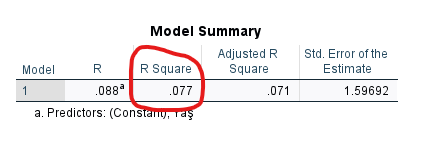
Son olarak “Model Summary” tablosunda, regresyon analizi sonucunda bulduğumuz, yaş ile mutluluk arasındaki istatistiksel olarak anlamlı ilişkinin etki büyüklüğüne bakacağız. Buna “R Square” değerinden bakıyoruz.

R Square değeri, her zaman “Model Summary” tablosundaki R değerinin karesine eşittir. Bu R değeri de, “Coefficients” tablosundaki Beta değerine eşittir.

Bu örnekte R Square yani R Kare değeri 0.077 çıktı. Bu, bir insanın kaç yaşında olduğunun, o insanın mutluluk seviyesini %7.7 oranında açıkladığını gösteriyor. Diğer %92.3 farklı sebeplerle açıklanıyor. R Kare değeri yorumlama hakkında daha detaylı bilgi öğrenmek için R Kare hakkında özel olarak yazdığım yazıyı okuyabilirsiniz.

SPSS ile doğrusal (lineer) regresyon analizi yapma adımları bu kadardı. Önce varsayımları test ettik, sonra SPSS ile analizi yaptık, en son olarak da SPSS’in bize verdiği tabloları yorumladık. Artık regresyon analizini raporlama aşamasına geçebiliriz.