SPSS ile Fisher’s Exact Test (Resimli)

Fisher’s Exact Test, küçük örneklemlerde, iki kategorik değişken arasındaki ilişkiyi değerlendirmek için etkili bir araçtır. Bu blog yazısında Fisher’s Exact Test’in ne olduğunu, testin varsayımlarını, SPSS ile nasıl yapılacağını ve analiz sonuçlarının nasıl yorumlanması gerektiğini ele alacağız. Ayrıca, ki kare testi ile Fisher’s Exact Test’in arasındaki farklara değineceğiz.

Fisher’s Exact Test Nedir?

Fisher’s Exact Test, adını Ronald Fisher’dan almıştır ve ilk kez 1922 yılında yayınlanmıştır. Bu test, kategorik veriye sahip iki grup arasındaki ilişkiyi değerlendirmek için bir analiz yöntemidir. Bu açıdan Ki Kare Testi’ne benzemektedir. Fisher’s Exact Test, küçük örneklemlerde kullanılmak üzere tasarlanmıştır ve özellikle 2×2 tablo analizi için en uygundur.

Fisher’s Exact Test, parametrik olmayan bir testtir ve verilerin dağılımının herhangi bir özel dağılıma uyması gerekmeksizin kullanılabilir.

Bir Fisher’s Exact Test yaparken, sıfır hipotezi H0 olarak tanımlanır. H0 hipotezi, iki değişken arasında bir ilişkinin olmadığını ifade eder. Alternatif hipotez H1 olarak adlandırılır ve iki değişken arasında bir ilişkinin olduğunu iddia eder. Test istatistiği, verilerinizin gözlemlenen değerleri ile beklenen değerleri arasındaki farklar dikkate alınarak hesaplanır.

Fisher’s Exact Test vs. Ki Kare Testi Farkları

Fisher’s Exact Test de, aynı Ki Kare Testi gibi kategorik verilerin analizinde kullanılmaktadır. Peki ama neden kategorik verilerin karşılaştırılması için 2 farklı test var? Fisher’s Exact Test’in Ki Kare Testi’nden en büyük ayırt edici özelliği, küçük örneklemden oluşan veri setlerinde kullanılmasının daha uygun olmasıdır. Aşağıda Fisher’s Exact Test’in Ki Kare Testi’ne göre avantajları ve dezavantajlarından bahsediyorum.

Fisher’s Exact Test’in Ki Kare Testi’ne göre bazı avantajları vardır:

• Hesaplama yöntemi kesin olduğu için, küçük örneklemlerde kullanılabilir ve sonuçlar güvenilirdir.
• Ki Kare Testi’nin varsayımlarından biri olan, her hücredeki gözlem sayısının en az 5 olma gerekliliği, Fisher’s Exact Test için geçerli değildir. Bu yüzden verideki kategorilerin kesişim tablosundaki bazı kategorilerin kesişim hücrelerindeki kişi sayıları 0 olsa bile kullanılması uygundur (Ki Kare Testi’ni bu durumda kullanamazdık).
• İstenilen düzeyde anlamlılık elde etmek için daha az gözlem sayısı gerektirir.

Tabii ki, Fisher’s Exact Test’in bazı dezavantajları da vardır:

• Büyük örneklemlerde hesaplama süresi uzun olabilir. Örneklemdeki kişi sayısı arttıkça Ki Kare Testi, daha efektif olarak hesaplama yapar.
• The Fisher’s Exact Test, en iyi 2×2 tablolar için uygundur. 3×2, 3×3 veya daha büyük tablolarla çalışırken Ki Kare Testi, yeterince isabetli sonuçları Fisher’s Exact Test’ten daha efektif bir şekilde verebilmektedir.
• Kategori sayısı büyüdükçe, Fisher’s Exact Test sonuç tablolarını yorumlamak zorlaşır.

SPSS ile Fisher’s Exact Test Nasıl Yapılır?

Bu örneğimizde, 20 kişiden oluşan bir grubun, medeni durumlarıyla (evli – bekar) cinsiyetleri (kadın – erkek) arasında bir ilişki var mı diye bakacağız.

SPSS’te Fisher’s Exact Test yapma adımları, Ki Kare Analizi gibidir. Analyze -> Descriptive Statistics -> Crosstabs butonlarına basıyoruz.

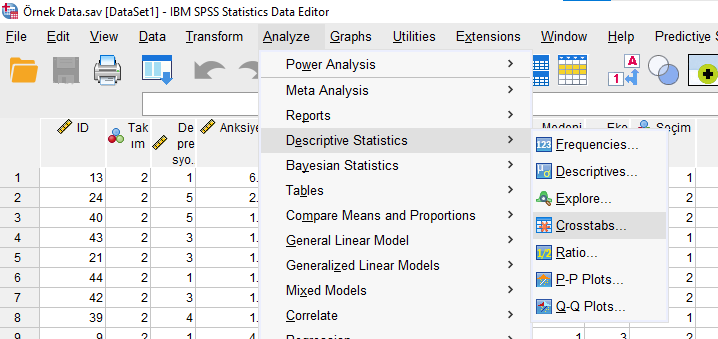
Bir kategorik değişkenimizi Rows, diğerini Columns’a atıyoruz. Hangisini nereye attığımız fark etmez. “Statistics”e basıp “Chi-Square”i işaretliyoruz. Ki Kare testi yapmayacağız ama Fisher’s Exact Test sonucunu SPSS’in bize göstermesini sağlamak için bunu işaretlemek gerekiyor.

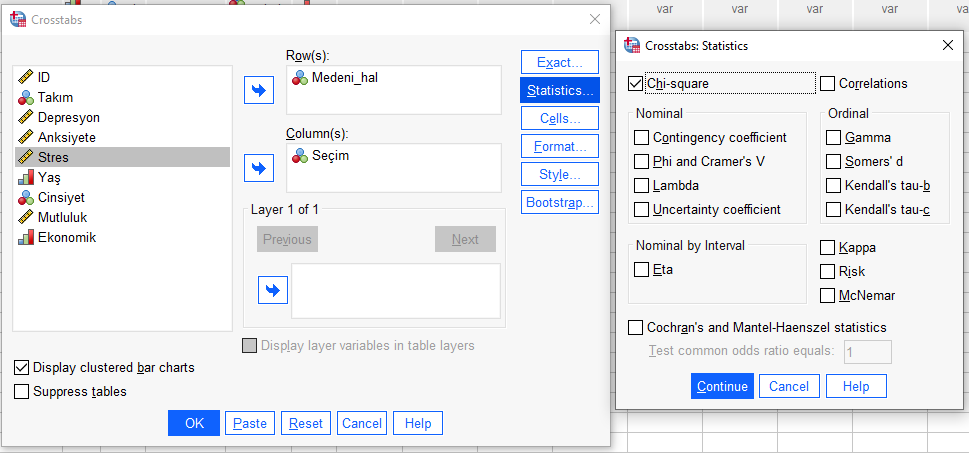
Fisher’s Exact Test Yorumlama

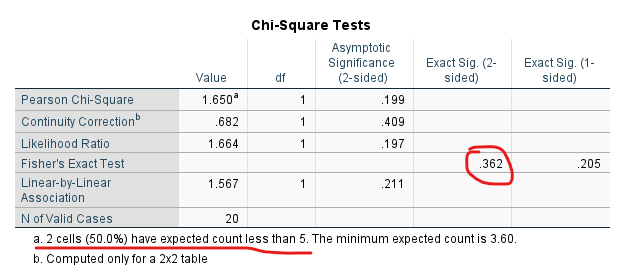
SPSS’in bize göstereceği tablolardan Chi-Square Tests başlıklı tabloda, Fisher’s Exact Test satırındaki Exact. Sig (2-sided) sütunundaki değer, Fisher’s Exact Test’imizin p istatistiksel anlamlılık değerini göstermektedir. Bu örnekte p = 0.362 olduğu yani 0.05’ten büyük olduğu için, gruplar arasında istatistiksel olarak anlamlı bir ilişki bulunmamaktadır sonucuna varıyoruz.

Tablonun altında dikkat ederseniz “a. 2 cells (50%) have expected count less than 5” yazıyor. Fisher’s Exact Test değil de Ki Kare Testi sonucuna güvenmek için, 5’ten aşağı kişi içeren hiç hücre olmaması gerekmektedir. Eğer bu örnekte yazan yerine “0 cells have expected count less than 5” yazsaydı, o zaman analiz sonucunu ilk satırdaki Pearson Chi-Square satırının Asymptotic Significance sütunundan okuyacaktık. Fakat bu örneğimizde 5’ten az kişiye sahip olan 2 hücre olduğu için Ki Kare yerine Fisher’s Exact Test sonucunu okuduk.

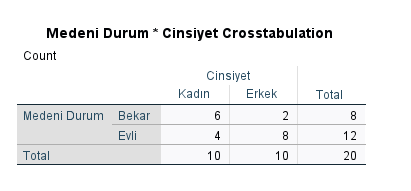
Hangi cinsiyette ve medeni durumda kaçar kişi varmış görmek için de Crosstabulation tablosuna bakabiliriz. Bu tabloya göre, Bekar 6 Kadın, Bekar 2 Erkek, Evli 4 Kadın, Evli 8 Erkek varmış. Bekar Kadın olmak ve Evli Erkek olmanın daha yaygın olduğu görülüyor, fakat Fisher’s Exact Test’imizin sonucu 0.05’ten büyük yani istatistiksel olarak anlamsız çıktığı için, “Medeni Durum ve Cinsiyet arasında bir ilişki saptanmamıştır. Görülen bütün farklılıklar, şans eseri oluşuyor gibi görünmektedir.” şeklinde bir sonuca varıyoruz.