Polinom (Eğrisel) Regresyon — SPSS (Resimli)

Polinom (eğrisel) regresyon, SPSS gibi istatistiksel analiz araçlarıyla veri setlerindeki ilişkileri incelemek ve tahminler yapmak için sıkça kullanılan bir tekniktir. Bu yöntem, doğrusal regresyonun sınırlı kaldığı durumlarda daha esnek bir model oluşturmak için kullanılır. Genellikle, bir bağımsız değişken ile bağımlı değişken arasındaki ilişki, doğrusal olmayan bir şekilde modellenebilir. Polinom regresyon, bu tür ilişkileri modellemek için kullanılan etkili bir yaklaşımdır. Bu yazıda, SPSS kullanarak polinom regresyonun temel prensiplerini, uygulanmasını ve sonuçlarının yorumlanmasını ele alacağız.

Polinom (Eğrisel) Regresyon Nedir?

Polinom regresyon yani eğrisel regresyon, doğrusal regresyonun genişletilmiş versiyonu olarak düşünülebilir ve değişkenler arasında basit bir doğrusal ilişkiden daha karmaşık ilişkiler olduğu durumları modellemek için kullanılır. Veriler arasındaki ilişkinin doğrusal olmadığı durumlarda kullanılır. Bu yöntem, veriler arasındaki korelasyonu temsil etmek için bir polinom kullanır. Bu polinom, veri noktalarının dağılımına en iyi şekilde uyan eğriyi bulmak için kullanılır.

Türkçe’de “polinom regresyon”, “polinomal regresyon”, “eğrisel regresyon” terimleri kullanılırken İngilizce’de “polynomial regression” ve “curvilinear regression” terimleri kullanılmaktadır. İkinci dereceden bir polinomal fonksiyon modeli için “quadratic model” terimi kullanılıyor.

Doğrusal regresyon ile karşılaştırıldığında, polinomal regresyon daha karmaşık ilişkileri modelleyebilir. Doğrusal regresyon, yalnızca veriler arasındaki ilişkinin doğrusal olduğu durumlarda etkilidir; yani, bir bağımsız değişkenin artması veya azalması, bağımlı değişken üzerinde doğrusal bir etkiye sahiptir. Ancak, polinomal regresyon, veriler arasındaki ilişkinin doğrusal olmadığı durumlar için daha uygundur. Örneğin, veriler arasında ikinci dereceden veya daha yüksek dereceden bir ilişki varsa, polinomal regresyon kullanılabilir.

Matematiksel olarak, doğrusal (lineer) regresyon modeli genellikle şu şekilde ifade edilir:

y = a + bx

Polinomal (eğrisel) regresyon ise genellikle aşağıdaki gibi ifade edilir:

y = a + bx + cx² + dx³ + …

Burada, x’in üzerindeki en büyük sayı polinomun derecesini temsil eder ve x’in önündekiler katsayılarıdır. Bu model, doğrusal regresyon modelinin genellemesidir ve daha karmaşık ilişkileri temsil edebilir.

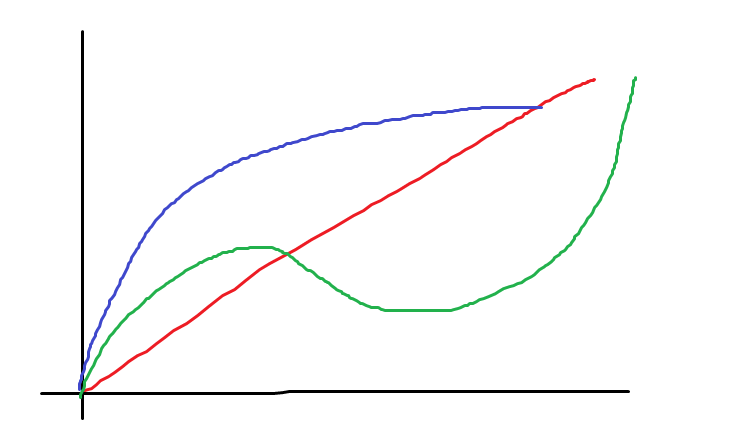
Aşağıdaki örnekte, kırmızı çizgi 1. dereceden bir polinomu yani doğrusal bir ilişkiyi temsil eder. Mavi çizgi, 2. dereceden bir polinomu yani eğrisel bir ilişkiyi temsil eder. Yeşil çizgi de 3. dereceden bir polinomu temsil eder. Mavi çizgide bir tane dönüm noktası, yeşil çizgide ise iki tane dönüm noktası olduğuna dikkat edin. Bu yüzden biri 2. derece diğeri 3. derece polinom olduğunu ayırt edebildik.

SPSS ile Polinom (Eğrisel) Regresyon Analizi Nasıl Yapılır?

Bu örnekte, bir gruptaki insanların zeka skoru ile dersteki başarı seviyeleri arasındaki ilişkiyi SPSS ile polinom regresyon analizi uygulayarak değerlendireceğiz. Basit olması adına bu sayfada yalnızca 2. dereceden (ve en son çok kısa 3. dereceden) polinomların regresyon modelini inceleyeceğiz, fakat bu sayfada öğrendiğiniz metodu daha yüksek dereceli polinomlarla da uygulayabilirsiniz. Ayrıca, sosyal bilimlerde ve doğada bir ilişki eğer doğrusal değilse genelde en fazla 2. dereceden polinom oluyor, daha büyük dereceli polinom olmuyor. Bu yüzden 2. dereceden polinom ile eğrisel regresyon analizi yapmayı öğrenmeniz genellikle yeterli olacaktır.

Önce, analiz edeceğimiz iki değişken arasındaki ilişkinin grafiğine bakalım. Doğrusal bir ilişki mi var yoksa eğrisel bir ilişki mi var bunu görelim ki analize öyle başlayalım.

Graphs -> Scatter/Dot

Simple Scatter

Bağımlı değişkeni Y Axis, bağımsız değişkeni X Axis’e koyuyoruz.

Zeka seviyesi ile Başarı’nın ilişkisi bu şekilde. Noktaların dağılımına bakarsanız, doğrusal bir ilişkiden ziyade, zeka seviyesi azdan ortaya yaklaştıkça arttığını, ama çok yüksek zeka seviyesine sahip insanların da genellikle başarısının azalmaya başladığını görebiliriz. Yani bu eğrisel ilişki grafiği 2. dereceden bir polinom fonksiyona benziyor.

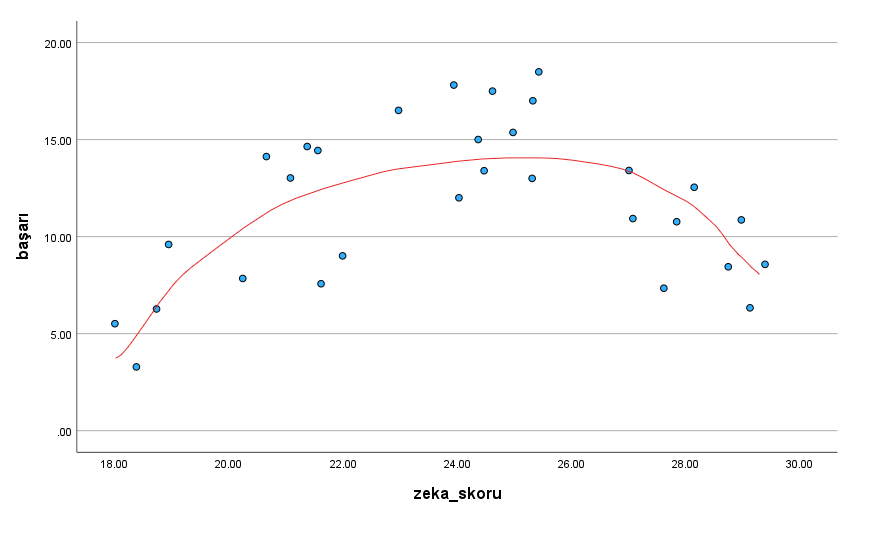
Şimdi 2. dereceden bir fonksiyon ile regresyon analizi yapmak istediğimiz için, bağımsız değişkenimizin 2. dereceden üssünü almamız gerekiyor.

Transform -> Compute Variable

Compute Variable penceresinde Target Variable bölümüne “değişkenin karesi” anlamına gelen yeni bir değişken ismi yazalım. Sonra, Numeric Expression bölümünde, “bağımsız değişken * bağımsız değişken” şeklinde bir formül kuralım. OK’a basalım.

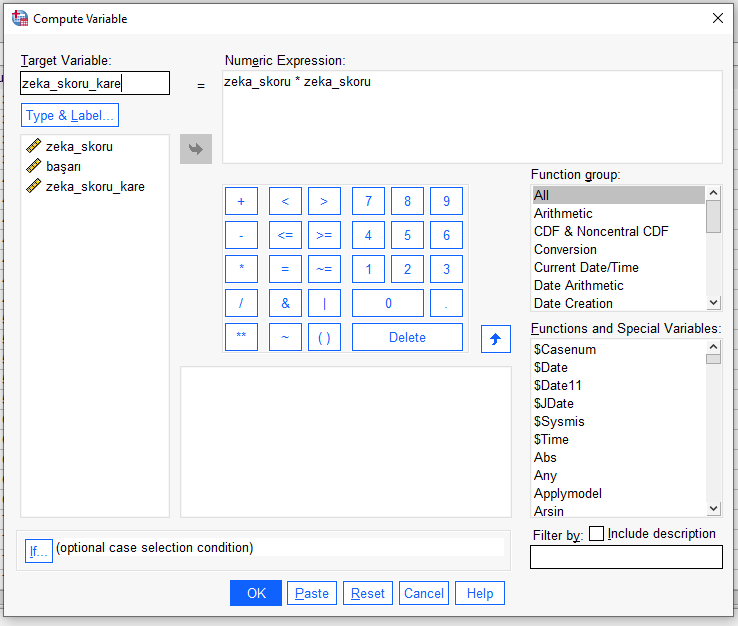
SPSS veri setimizin Data View kısmına gelirsek, en sağ sütunda yeni bir değişken açıldığını görebiliriz. Bu değişken, orijinal bağımsız değişkenin karesinin değerlerini gösterir.

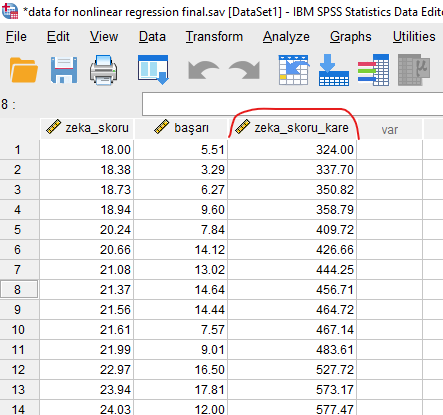
Şimdi, regresyon analizine başlayacağız.

Analyze -> Regression -> Linear

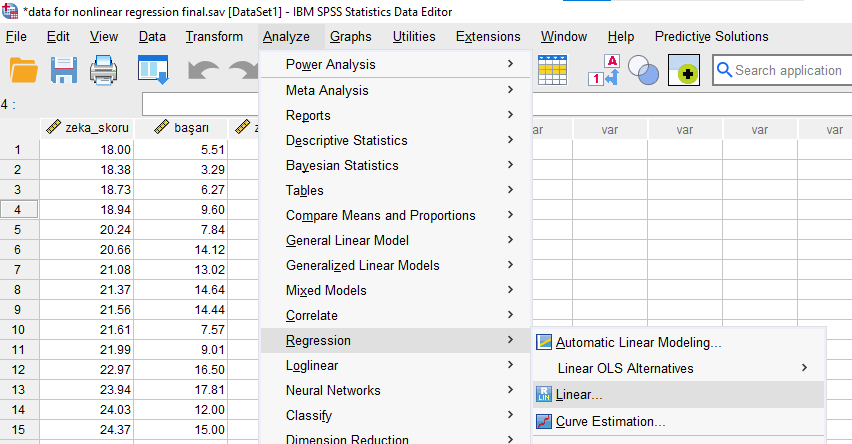
Önce, Dependent kutusuna bağımlı değişkeni, Independent kutusuna da orijinal bağımsız değişkeni yerleştirelim.

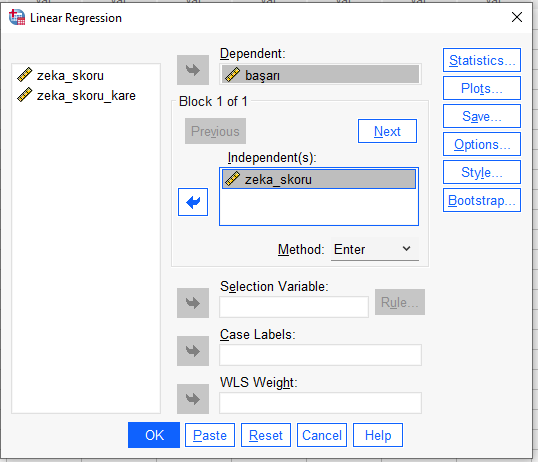
Sonra, “Next” butonuna basarak, bağımsız değişken kutusuna yeni oluşturmuş olduğumuz “zeka skorunun karesi” değişkenini de ekleyelim.

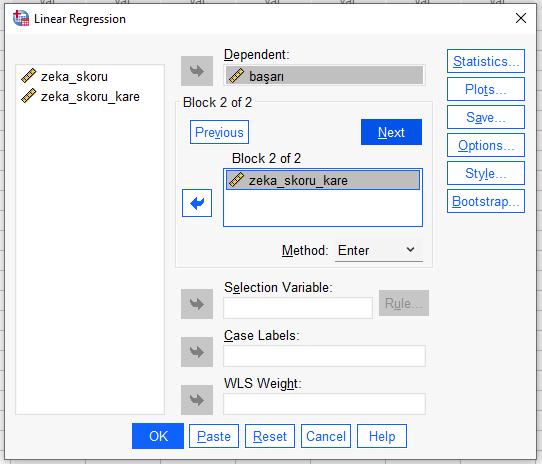
“Statistics” butonuna basarak “Estimates”, “Model fit” ve “R squared change”i işaretleyelim ve analizi başlatalım.

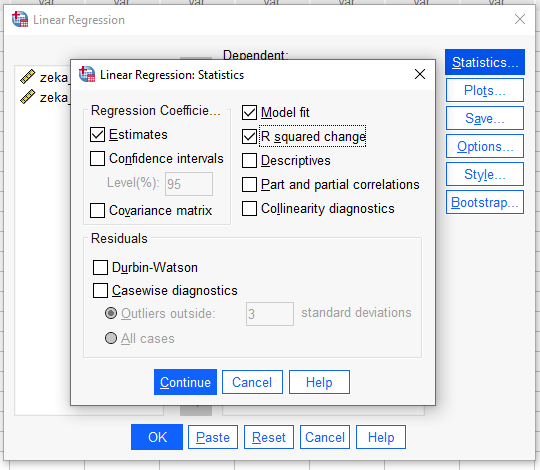
Polinom regresyon tablolarının yorumlanması, aynı hiyerarşik regresyon tablo yorumlamaya benzer.

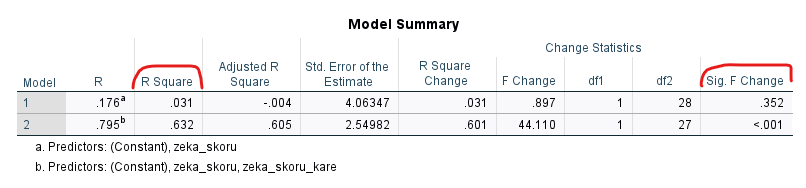
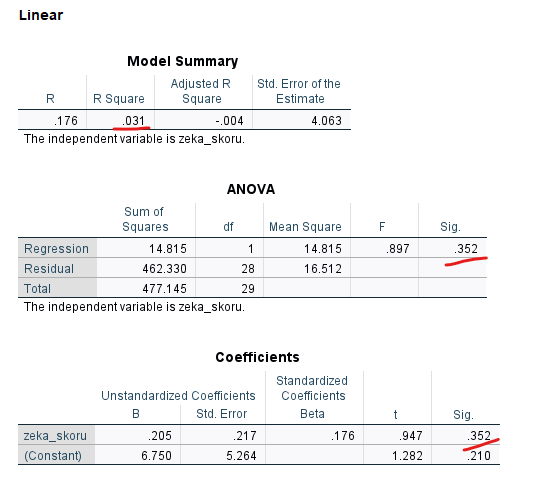
“Model Summary” tablosunda 1. satır yalnızca orijinal zeka skoru değişkeninin dahil edildiği doğrusal regresyon modelini temsil eder.

2. satır ise orijinal zeka skoruna ek olarak, zeka skorunun karesi değişkeninin de dahil edildiği polinom regresyon modelini temsil eder.

Buna göre 1. modelin p değeri 0.352 çıkmış ve bu model gözlemlenen varyansın yalnızca %3.1’ini açıklayabiliyormuş. Doğrusal olan 1. modelde istatistiksel olarak anlamlı bir ilişki yok demek oluyor.

2. modelin ise p değeri 0.001’den küçüktür yani istatistiksel olarak anlamlı bir ilişki var demek. R Square değeri de 0.632 yani bu model başarı’da gözlemlenen varyansın %63.2’sini açıklıyormuş. Demek ki polinom (eğrisel) regresyon modelimiz, lineer regresyon modeline göre, başarı’daki varyasyonu daha iyi şekilde açıklayabiliyormuş.

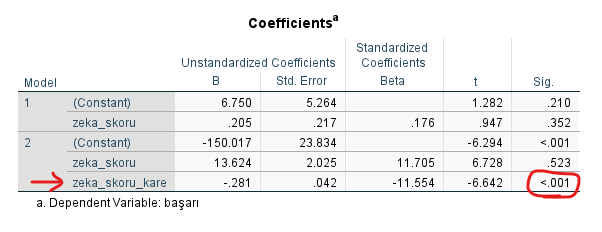
“Coefficients” tablosunda da, zeka skorunun tek başına dahil olduğu lineer modelde istatistiksel anlamlılık olmadığını (p = 0.352), hem zeka skorunun kendisinin hem de karesinin dahil olduğu polinom modelde ise zeka skorunun kendisinin istatistiksel olarak anlamlı etkisi olmadığını (p = 0.523) fakat zeka skorunun karesinin istatistiksel olarak anlamlı etkisi olduğunu görebiliyoruz.

Regression -> Curve Estimation Yöntemi ile SPSS’te Polinom Regresyon

Polinomal Regresyon Analizi’ni, SPSS’te ikinci bir yöntem ile de yapabiliriz. Bu şekilde, deminki yaptığımız regresyon analizinin de sağlamasını yapmış olacağız.

Analyze -> Regression -> Curve Estimation

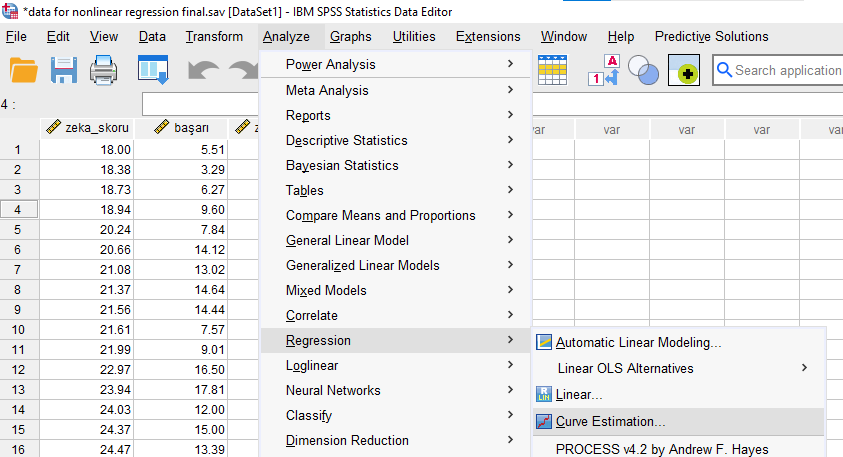
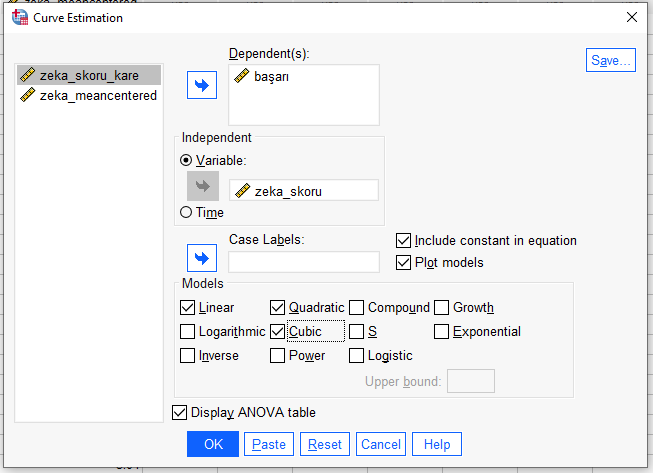
Açılan pencerede bağımlı değişkenimizi Dependent kutusuna yerleştiriyoruz. Orijinal zeka skoru değişkenimizi de (karesini değil) Independent kutusuna yerleştiriyoruz. Sonra, Models bölümünde Linear, Quadratic ve Cubic seçeneklerini işaretleyelim. Bunlar sırasıyla doğrusal (1. dereceden polinom), 2. dereceden ve 3. dereceden polinom modellerine karşılık gelmektedir.

Display ANOVA Table da işaretlersek sonuçları karşılaştırırken faydasını görürüz.

“Linear” başlıklı bölümdeki tablolarda, sadece zeka skoru’nun bağımsız değişken olarak ele alındığı doğrusal regresyon modelini görüyoruz. Dikkat ederseniz bu deminki 1. model ile aynı doğrusal regresyon modeli.

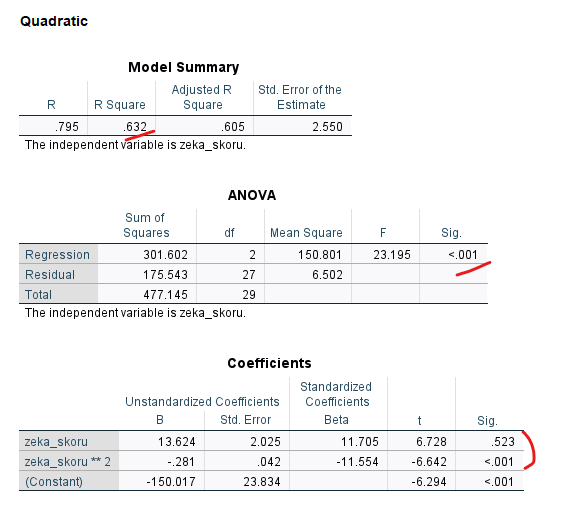
“Quadratic” başlıklı bölümde ise, 2. dereceden polinom fonksiyonun regresyon modelini görebiliyoruz. Buradaki de R Square ve Sig. p değerleri, deminki 2. modelin bire bir aynısı.

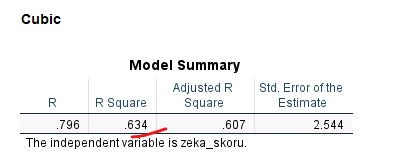
“Cubic” başlıklı bölümde 3. dereceden polinom ile oluşturulan regresyon modelini görüyoruz. Buradaki “Model Summary” tablosuna bakarsak, deminki 2. dereceden polinomun regresyon modelinin R Square değeriyle (0.632) aşağıdaki R Square’in (0.634) neredeyse eşit olduğunu görüyoruz. Yani, 2. dereceden polinomu 3. dereceden polinom yaparak regresyon modeli oluşturmak, bağımlı değişkendeki varyasyonun açıklanması konusunda neredeyse hiç faydalı olmamış.

O zaman, diyoruz ki “Demek ki 2. dereceden polinom ile oluşturulan polinomal (eğrisel) regresyon modeli en isabetli olan modeldir.”

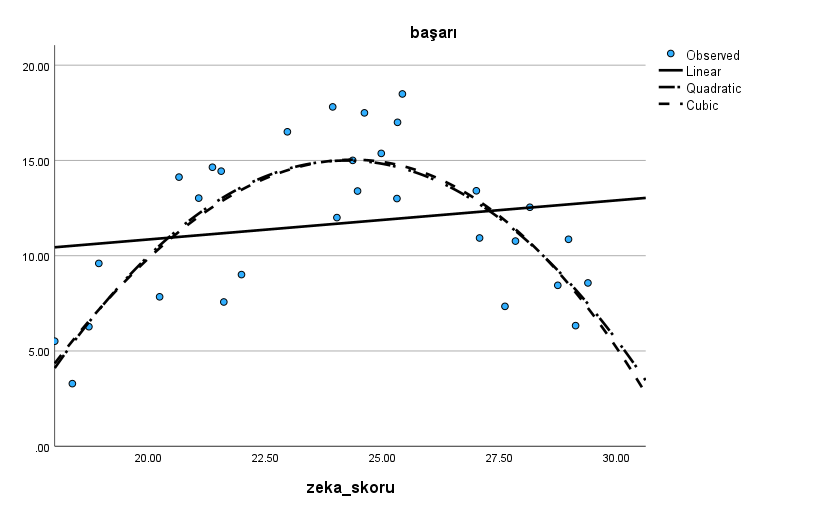
Son olarak, Curve Estimation bölümünden yaptığımız polinomal regresyon analizi sonucunda aşağıdaki gibi güzel bilgilendirici bir nokta grafiği elde edebiliyoruz. Doğrusal (Linear), ikinci dereceden (Quadratic) ve üçüncü dereceden (Cubic) polinomal regresyon modellerinin en iyi uyum çizgilerini (line of best fit) grafikte görebilirsiniz.

Burada da görebileceğiniz gibi, Linear uyum çizgisi noktaların dağılımına pek iyi uymuyor. Quadratic çizgisi ise epey uyuyor. Cubic çizgisi de uyuyor, fakat Quadratic’in neredeyse aynısı. Böyle bir durumda daha basit olan Quadratic polinomal regresyon modelinin çizgisini kullanmak tercih edilmelidir.