Cox Regresyon Analizi (SPSS)

Cox Regresyon Analizi, bir olayın belirli bir zaman dilimi içinde gerçekleşmesinin olasılığını etkileyen değişkenlerin incelenmesinde kullanılan bir sağkalım analizi (survival analysis) yöntemidir. Bu yazıda, Bu yazıda, Cox Regresyon Analizi’nin temel prensipleri, SPSS ile Cox Regresyonu yapma ve analiz sonuçlarının yorumlanması konularını ele alacağız.

Cox Regresyon Analizi Nedir?

Cox Regresyon Analizi, özellikle sağkalım analizlerinde kullanılan bir tür regresyon modelidir. Cox Regresyon Analizi’nin temel amacı, bir olayın gerçekleşmesinin gözlemlendiği zaman dilimi içinde (sağkalım süresi gibi) bir durumun yaşanma olasılığını (hastalığa yakalanma gibi) etkileyen faktörleri belirlemektir. Bu faktörler genellikle bağımsız değişkenler olarak adlandırılır ve analizde bağımlı değişkenin zamanla nasıl değiştiğini açıklamak için kullanılırlar.

Bu yöntem, özellikle sağlık alanında, hastalıkların risk faktörlerini ve bunların hastalığın gerçekleşme olasılığı üzerindeki etkisini değerlendirmek için ya da çeşitli durumların bir bireyin ölüm zamanını etkileyip etkilemediğini belirlemek için yaygın olarak kullanılır. Örneğin, bir hastalığın gelişme riskini etkileyen faktörleri belirlemek için Cox Regresyon Analizi kullanılabilir, bu durumda bağımsız değişkenler sigara kullanımı, alkol kullanımı ve araştırmanın başında bireyin sorumluluk test ölçeğinden aldığı skor olabilir.

Cox Regresyon Analizi, parametrik olmayan bir yöntemdir, yani verilere belirli bir dağılım varsayımı yapmaz. Bu özelliği, aynı lojistik regresyon gibi, çeşitli alanlardan gelen gerçek verilerin analizinde son derece kullanışlıdır.

Cox Regresyon Analizi sırasında, modelin temelinde bir risk oranı (hazard ratio) hesaplanır. Bu oran, belirli bir faktörün olayın gerçekleşme hızı üzerindeki etkisini ölçer. Hazard ratio’nun 1’e yakın olması, faktörün olayın gerçekleşme hızı üzerinde nötr bir etkiye sahip olduğunu gösterirken, 1’den büyük veya küçük olması, sırasıyla pozitif veya negatif etki anlamına gelir.

Cox Regresyon modeli, zamana bağlı eşit risk oranı varsayımı üzerine kurulur, yani Cox Regresyon ile analiz edilen bağımsız değişkenlerin, gözlemlenen sonuca etkisi, zaman geçtikçe değişmemelidir, etki hep aynı kalmalıdır. Buna SPSS’te analizi yaparken değineceğiz.

Cox Regresyon Analizi’nde incelenen veride, yalnızca 2 olasılığın gerçekleşme ihtimali vardır: ölüm-hayatta kalma, hastalık nüksetmesi-nüksetmemesi gibi. Ayrıca, gözlemlenen bütün katılımcıların deneyin en başından itibaren gözlemleniyor olduğu varsayılarak analiz yapılır.

SPSS ile Cox Regresyon Analizi Nasıl Yapılır?

Bu örnekte, 30 hafta boyunca gözlemlemiş olduğumuz bir hasta grubunun 30 hafta içindeki zamana bağlı ölüm ihtimallerini etkileyen faktörleri öğrenmek için Cox Regresyon Analizi yapacağız. Potansiyel etkisini incelediğimiz faktörler sigara içme durumu (evet-hayır), tedavi grubu (Grup 1-2-3) ve başlangıçtaki semptom şiddeti miktarıdır (1 ile 5 arasında ölçekte değişen değerler). Yani 2 kategorik, 1 de sürekli veri tipinde bağımsız değişkenimiz var.

SPSS ile Cox Regresyon Analizi yapmaya geçmeden önce, SPSS verimizin neye benzediğini SPSS üzerinde göstermek istiyorum. ID deneydeki kişinin kişi numarası. Hafta sütunu bir kişinin hangi haftaya kadar gözlemlenmiş olduğunu gösteriyor. Olay sütununda 1 görünmesi, kişinin 30 haftalık gözlem süresi içinde ölmüş olduğunu gösteriyor. Bu sütunda 0 yazsaydı kişi 30 hafta sonunda ölmemiş demek oluyor. Bu sütunun yanındaki diğer 3 sütun ise, bağımsız değişkenlerimizin kişiye göre aldığı değerleri belirtiyor.

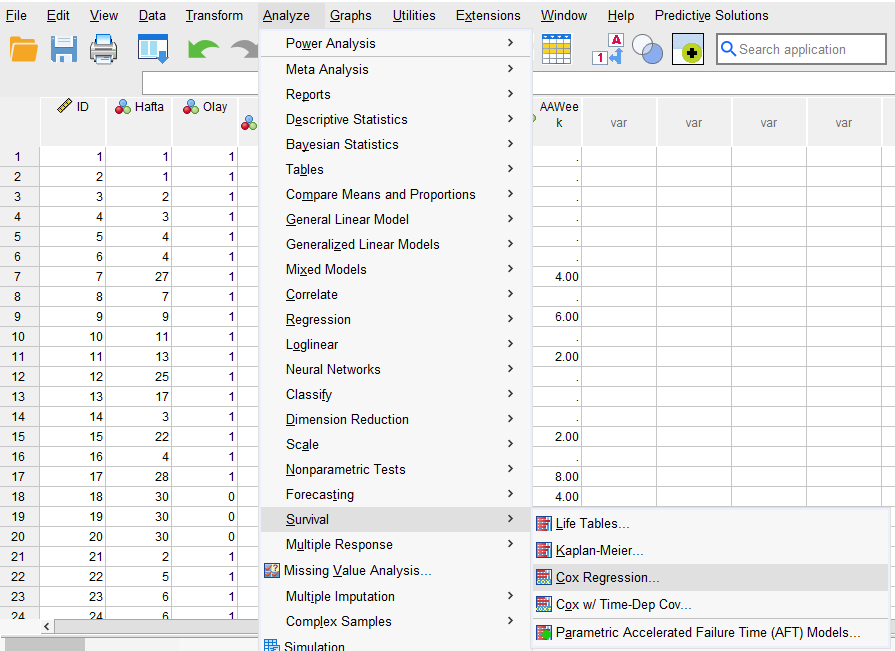
SPSS ile Cox Regresyon Analizi yapmak için, Analyze -> Survival -> Cox Regression butonlarına basıyoruz.

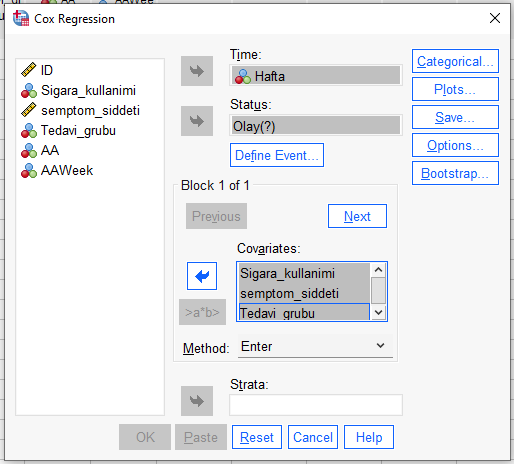
Açılan pencerede zaman değişkenimizi Time kutusuna, olayın gerçekleşip gerçekleşmediğini gösteren değişkenimizi Status kutusuna, etkisini incelemek istiyor olduğumuz bağımsız değişkenleri de Covariates kutusuna atıyoruz.

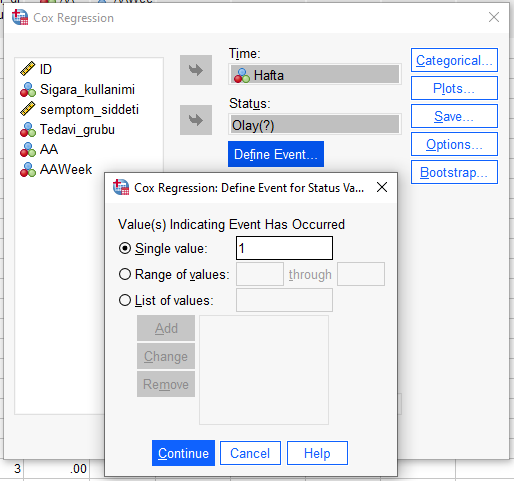
Olay değişkeninde, hangi numaranın Olay’ın (bu örnekte ölüm’ün) yaşandığını gösterdiğini SPSS’e öğretmek için “Define Event”e basıyoruz. Bizim örneğimizde 0 ölüm’ün gerçekleşmediğini, 1 ise katılımcının öldüğünü gösteriyor. Bu yüzden 1 yazıyoruz buraya.

SPSS’e aynı zamanda, hangi değişkenlerin kategorik olduğunu öğretmek gerekiyor. Bu yüzden bağımsız değişkenleri Covariates kutusuna koyduktan sonra “Categorical”a basıyoruz. Açılacak yeni pencerede, kategorik değişkenlerimizin hepsini Categorical Covariates kutusuna atıyoruz ve Reference Category bölümünden referans kategorimizi seçiyoruz. First dersek, o değişkende en küçük numara ile kodlanan kategori referans kategorisi olacak. Bunun pratik olarak anlamını az sonra göstereceğim.

Eğer sadece 2 kategoriden oluşan ve kategorileri 0 ve 1 ile kodlanmış bir kategorik değişken varsa, onu SPSS’e ayrıca tanıtmak zorunda değiliz. Fakat diğer bütün kategorik değişkenleri burada gösterdiğim şekilde tanıtmak zorundayız.

Son olarak “Options”a basıp CI for exp(B) işaretlersek sonuçları daha iyi görmemiz açısından yardımcı olur.

OK’a basıp SPSS’in analizi başlatmasını sağlayabiliriz artık.

Cox Regresyon Analizi Yorumlama

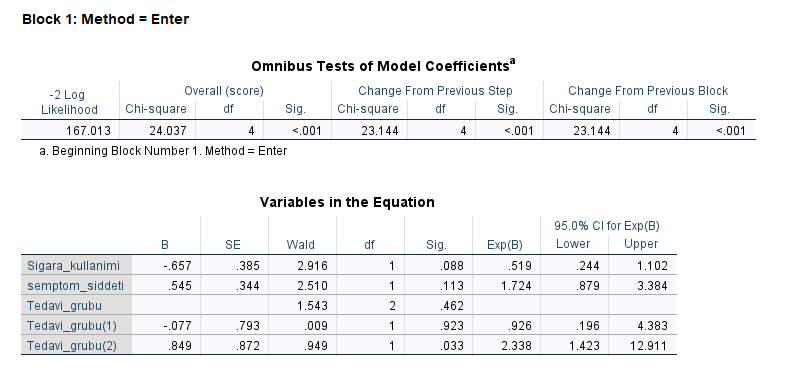
SPSS’in vereceği “Omnibus Tests of Model Coefficients” tablosundaki Sig. değeri, SPSS’in oluşturduğu Cox regresyon modelindeki en az 1 değişkenin bu deneydeki hastaların sağkalım zamanına anlamlı bir etkisi olduğunu gösteriyor.

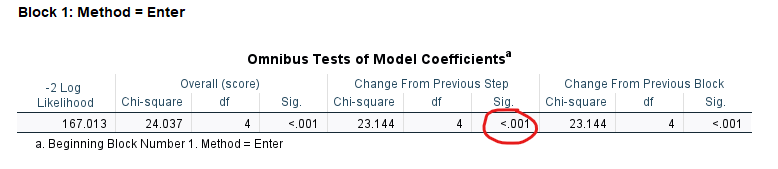
Hangi değişkenin anlamlı etkisi olduğunu görmek için “Variables in the Equation” tablosuna bakmak gerekiyor. Sig. sütununda görünen p değerleri 0.05’in altında olan değişkenler, sağkalım zamanına anlamlı bir şekilde etki etmiş. Sağkalım oranı yerine “tehlike oranı” anlamına gelen “hazard rate” terimi İngilizce Cox regresyon kaynaklarında sık kullanılmaktadır.

Bu tablodaki regresyon katsayıları, modeldeki bağımsız değişkenlerin bir fonksiyonu olarak beklenen olayının gerçekleşme tehlikesini tahmin eder. Bu tabloda pozitif bir B katsayısı değeri, bağımsız değişken ile terminal olayın gerçekleşme tehlikesi (bu örnekte ölüm) arasında pozitif bir ilişkiyi gösterir. Bu, bağımsız değişkendeki daha yüksek B değerlerinin daha düşük hayatta kalma süresiyle ilişkili olduğu anlamına gelir.

Exp(B) sütununda ise, bağımsız değişkende 1 birimlik değişimin sağkalım zamanında kaç birimlik değişime yol açtığı görünüyor. Buradaki exp(B), lojistik regresyondaki exp(B) ile aynıdır, buradaki tablo yorumlamayı daha iyi anlamak için o yazıma da bakabilirsiniz.

B sütunu, Cox regresyon katsayısını gösterir, Exp(B) sütunu ise aynı katsayıyı logaritma cinsinden gösterir. Pratik olarak işimize yarayan bilgi regresyon katsayısının logaritması alınmış olan şekli. B negatif çıkarsa Exp(B) 1’den küçük çıkar, B pozitif çıkarsa Exp(B) 1’den büyük çıkar.

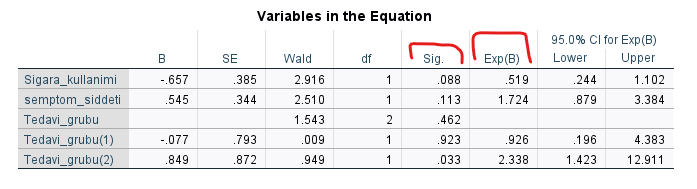
Her satırı yorumlayalım:

• Sigara kullanımı, hastaların sağkalım zamanları üzerinde anlamlı bir etkiye sahip değilmiş (p = 0.088). Eğer anlamlı etkiye sahip olsaydı Exp(B) değerine de bakarak diyecektik ki “Kategori numarası 0’dan 1’e geçerken azalma gerçekleşmiş. 1 ile kodlanmış olan sigara kullanmak, 0 ile kodlanmış olan kullanmama’ya göre, daha az ölüm riski taşımakta. Sigara kullananların ölme tehlikesi (sigara kullanmanın hazard rate’i), sigara kullanmayanların %51.9’u kadardır.”
• Semptom şiddeti de hastaların sağkalım zamanları üzerinde anlamlı bir etkiye sahip değilmiş (p = 0.113). Eğer anlamlı etkiye sahip olsaydı Exp(B) değerine de bakarak diyecektik ki “hastadaki her 1 puanlık semptom şiddeti artışı, o hastanın ölüm tehlikesini 1.724 kat arttırıyor.” Başka bir deyişle, “1. hafta ölçülen semptomları daha fazla olan bireylerin, daha az semptomu olanlara göre daha erken ölmeleri öngörülüyor.”

Tedavi Grubu bağımsız değişkeni için 3 satır var. Tablodaki tedavi grubu değişkenleri kukla değişkenlerdir. En üstte yer alan tedavi grubu değişkeni, referans kategorisini temsil eder ve kendisiyle ilişkili bir regresyon katsayısına sahip değildir. Analizin başından hatırlarsak, tedavi grubunun referans kategorisini en düşük sayıyla kodlanan kategori olarak ayarlamıştık. Yani Tedavi_grubu satırı Grup 1’i tek başına, Tedavi_grubu(1) satırı Grup 2’nin Grup 1 ile karşılaştırmasını, Tedavi_grubu(2) satırı da Grup 3’ün Grup 1 ile karşılaştırmasını temsil etmektedir bu tabloda.

•  Tedavi_grubu(1) satırındaki Sig. değeri 0.923 olduğu için anlamlı bir etki yok. Ama olsaydı Exp(B) sütununa bakarak diyecektik ki, “Tedavi grubu 2’de olmak, tedavi grubu 1’de olmaya göre %92.6 ölüm riski taşımaktadır.”
• Tedavi_grubu(2) satırındaki Sig. değeri 0.033 olduğu için anlamlı bir etki bulunmakta. Exp(B) diyebiliriz ki “Tedavi grubu 3’te olmak, tedavi grubu 1’de olmaya göre 2.338 kat daha yüksek ölüm riski taşımaktadır.”

Proportional Hazards (Orantılı Tehlikeler) Varsayımı Test Ederek Cox Regresyonu Gerçekleştirme

Cox regresyonu, gözlemlenen olaya ilişkin tehlike miktarı ile zaman arasındaki ilişkinin, ortak değişkenlerin seviyelerine bağlı (veya koşullu) olmadığını varsayar. Yani, olayın gerçekleşme tehlikesi, gözlem yapılan zaman dilimi içinde hep aynı seviyede olmalıdır.

Orantılı tehlikeler varsayımının karşılanıp karşılanmadığını test etmek için zaman ölçüsü ile Cox regresyon modelindeki ortak değişkenler arasındaki etkileşim test edilebilir. Varsayımın ihlal edilmesi durumunda, ilgili etkileşim terimlerini (orijinal bağımsız değişkenlerin yanı sıra) son Cox regresyon modelinize dahil etmek gerekir.

Cox regresyonu orantılı tehlikeler varsayımını kontrol etmek için en basit yöntem, önce orijinal ortak değişkenler kümesinin modele girildiği ve ardından ilgili değişkenlerin zaman ile etkileşimlerinin eklendiği hiyerarşik bir regresyon modeli oluşturmaktır.

Deminki yaptığımız Cox regresyon analizini, şimdi de “orantılı olasılık varsayımı”nı da test etmiş olarak gerçekleştirelim…

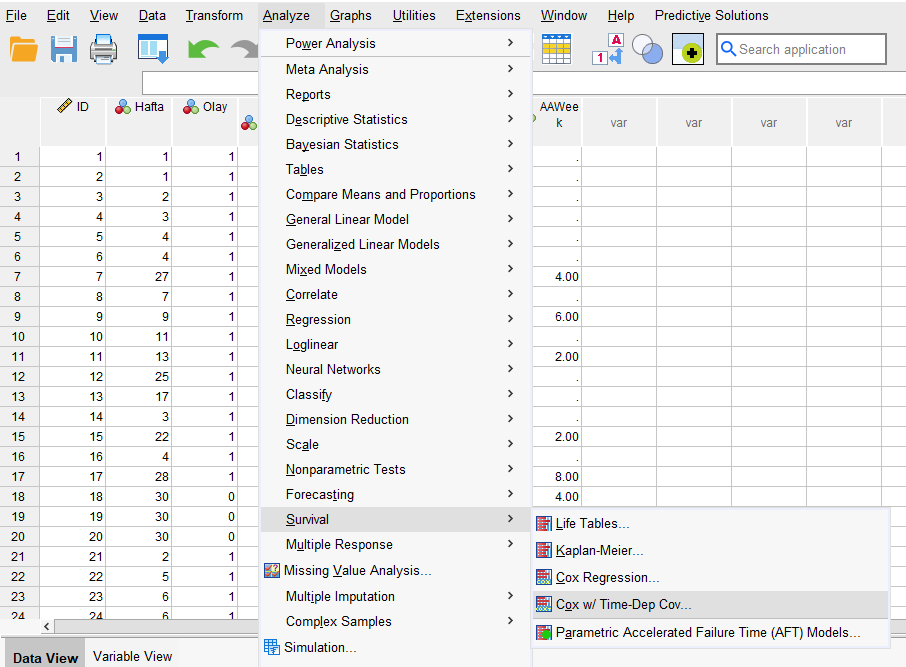
Analyze -> Survival -> Cox w/ Time-Dep Cov

Bu kısaltma “zamana bağımlı olan bağımsız değişken bulunduran Cox regresyonu” anlamına gelmektedir.

Soldaki kutudaki SPSS’in oluşturduğu yeni Zaman değişkenini sağdaki kutuya koyuyoruz. Sonra sağ üst köşedeki “Model” butonuna basıyoruz.

“Model”e bastıktan sonra deminki gibi yine bir Cox Regresyon penceresi açılacaktır. Bunu önce deminki analizimizdeki gibi dolduruyoruz değişkenlerimizle.

Yaptıktan sonra “Next” butonuna basıyoruz, buradan sonrası yeni işlemler, varsayım testini yapmak için.

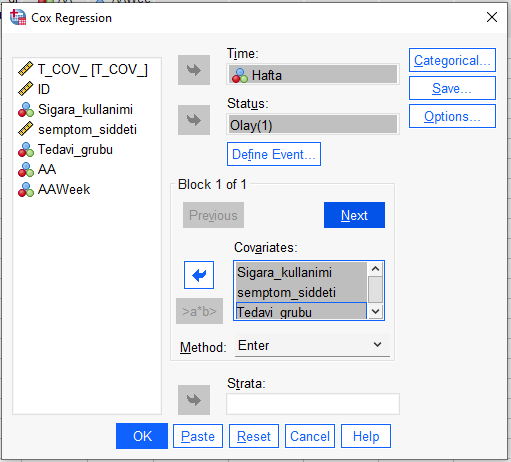
Soldaki kutuda, yeni oluşturulmuş olan zaman değişkeni ile birlikte bağımsız değişkenlerden birini seçerek (CTRL tuşu ile) “>a*b> butonuna basıp Block 2 of 2 yazan boş kutuya ekliyoruz.

Bütün bağımsız değişkenlerin zamanla ilişkisi için bunu yapıyoruz.

Artık analizi başlatabiliriz.

Block 1 bölümü içindeki SPSS tabloları, demin yaptığımız varsayım testi içermeyen analizde gelenlerle bire bir aynı tablolar şeklinde gelecektir.

Block 1 bölümü içindeki tablolar ise yeni tablolardır.

“Omnibus Tests of Model Coefficients” tablosundaki Sig. değeri, bağımsız değişkenlerin tek başlarına zaten var olarak bulunduğu Cox regresyon modeline, bağımsız değişkenlerin zamanla interaksiyonlarının eklendiği durumda, modelde istatistiksel olarak anlamlı bir değişim olup olmadığını gösteriyor. Bu örnekte p değeri 0.687 yani modelde anlamlı bir değişim yok. Bu şu anlama geliyor: “Bağımsız değişkenlerin hepsinin ölüm’ün gerçekleşme ihtimali üzerindeki tehlike oranı (hazard rate’i) zamana bağlı olarak değişmiyor. Yani deney boyunca ölüm’ün gerçekleşme olasılığı (ölüm riski), deneyin başından sonuna kadar aynı denebilir.”

Eğer bu tablodaki p değeri istatistiksel olarak anlamlı olsaydı, hangi değişkenlerin zamana bağlı olarak ölüm riski miktarının değiştiğini bulmak için altındaki “Variables in the Equation” tablosuna bakmak gerekecekti.

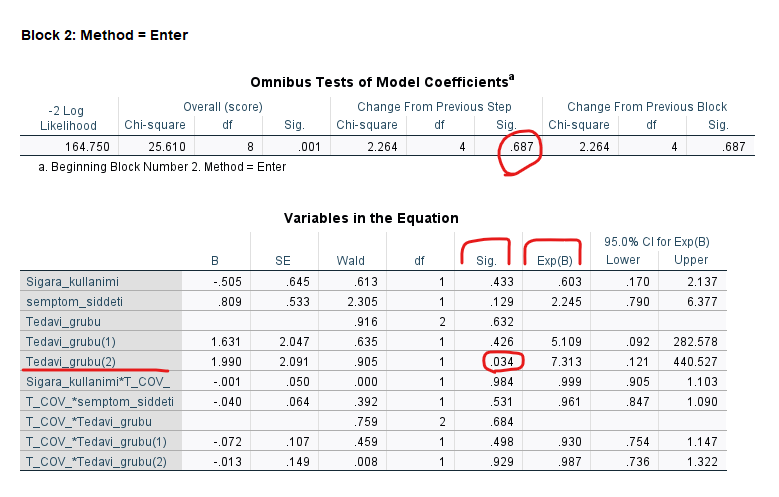
Eğer herhangi bir veya daha fazla bağımsız değişkenin zamanla olan etkileşiminin ölüm riski miktarı üzerinde istatistiksel olarak anlamlı bir etkisi bulunmuş olsaydı, yeni bir Cox regresyon analizi yapıp (ilk yaptığımız gibi) Cox regresyon analizi modeline o değişkeni de katmak gerekirdi ve sonuçları onun üzerinden okumak gerekirdi.

Cox Regresyon Analizi hakkında her şey bu kadardı. Bir hasta grubunun 30 haftalık bir gözlem süresi içindeki ölüm risklerini hangi değişkenler belirliyor diye görmek için SPSS’te Cox Regresyon Analizi yaptık. Önce sadece bağımsız değişkenlerin tek başlarına bulunduğu bir Cox regresyonu yaptık, sonra bağımsız değişkenlerin zamana bağlı olarak ölüm riskini değiştirip değiştirmediğini görmek için bağımsız değişken ve zamanın etkileşimlerini de Cox regresyonu modeline dahil ettik. Eğer zamana bağlı etkileşimlerin herhangi birinin anlamlı etkisinin olduğunu görmüş olsaydık o etkileşimi de modele katarak ilk yaptığımız gibi bir Cox regresyonu yapmamız gerekecekti ve en son o analizin sonuçları üzerinden yorumlama yapmamız gerekecekti. Okuduğunuz için teşekkürler.