SPSS ile Wilcoxon Signed-Rank Test (Resimli)

Bu sayfada, Wilcoxon Signed-Rank Test (Wilcoxon İşaretli Sıralar Testi) adlı istatistiksel testin ne olduğundan bahsedeceğim ve SPSS programını kullanarak nasıl Wilcoxon Signed-Rank Test yapıldığını ve sonuçların nasıl yorumlandığını resimlerle göstereceğim.

Wilcoxon Signed-Rank Test Nedir?

Wilcoxon Signed-Rank Test, aynı kişilerden oluşan bir grubun 2 farklı zamandaki ölçüm skorlarını karşılaştırmak için kullanılır. Bu testin bağımlı örneklem t-testinden farkı, parametrik olmayan bir test olmasıdır. Yani bu test, t-testinin normallik varsayımını karşılayamadığımız durumda t-testine alternatif olarak yapılır. Aynı zamanda, bağımlı değişkenin veri tipinin ordinal veri tipi olduğu durumlarda da Wilcoxon Signed-Rank Test yapılır.

Eğer aynı kişilerin 2’den fazla farklı zamandaki ölçüm skorlarını karşılaştırmak istiyorsak, Wilcoxon Signed-Rank Test yerine Friedman Testi yapmamız gerekir.

Wilcoxon Signed-Rank Test, Wilcoxon Rank-Sum Test olarak bilinen başka bir test ile karıştırılmamalıdır. Bu ikisi farklı testlerdir ve farklı amaçlara hizmet ederler.

Wilcoxon Signed-Rank Test Varsayımları

Wilcoxon Signed-Rank Test uygulamak için verinin normal dağılım göstermesi gerekmez. Fakat, çok çarpık olmayan, yaklaşık olarak simetrik bir dağılım göstermesi gerekir. Eğer simetrik bir dağılım da göstermiyorsa, o zaman Wilcoxon Testi yerine İşaret Testi uygulamak daha uygun olacaktır.

SPSS ile Wilcoxon Signed-Rank Test Nasıl Yapılır?

Bu örnekte 52 kişilik bir katılımcı grubunun bir ilaç almadan önceki ve ilacı aldıktan sonraki kalp atış hızları arasında anlamlı farklılık var mı diye bakmak için Wilcoxon Signed-Rank Test yapacağız.

Aşağıdaki adımları izleyerek SPSS üzerinde Wilcoxon Signed-Rank Test yapabiliriz:

Adım 1:

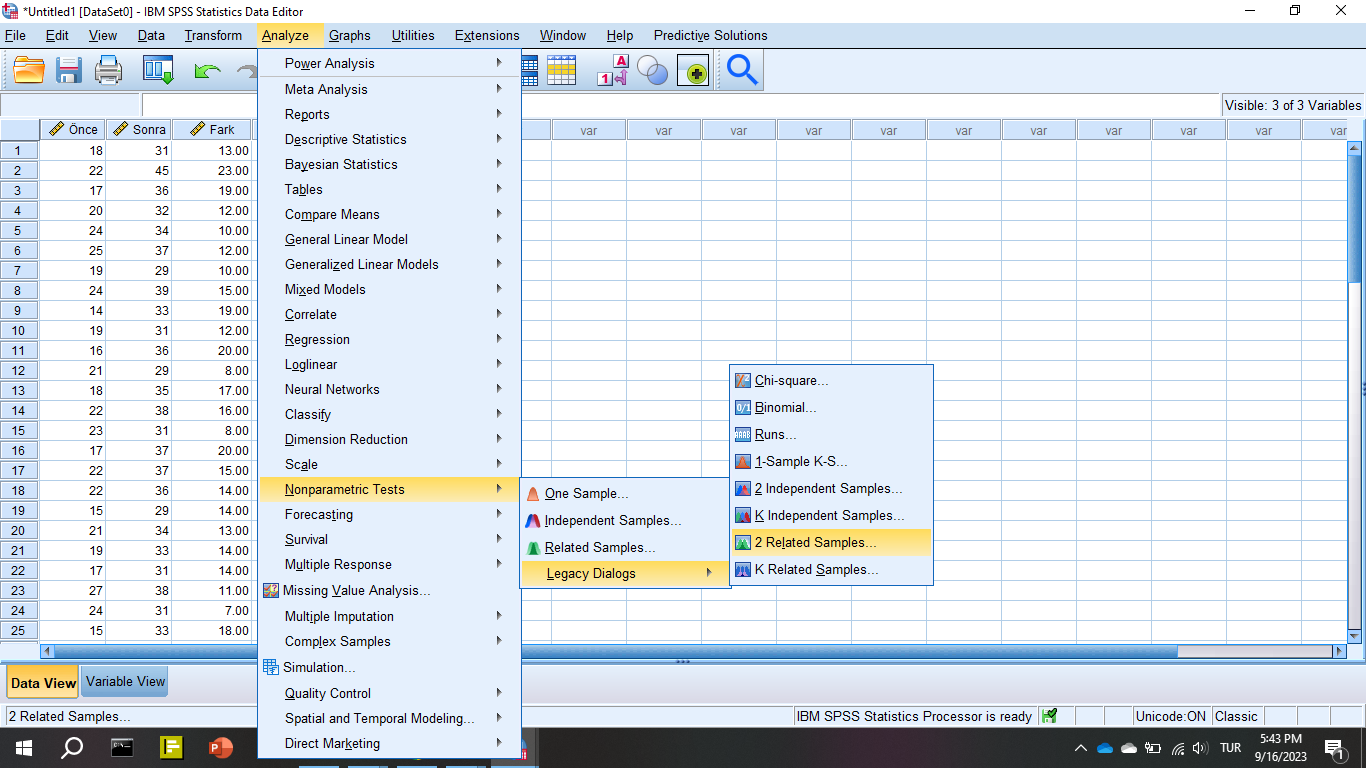
Öncelikle, SPSS’te Analyze -> Nonparametric Tests -> Legacy Dialogs -> 2 Related Samples butonlarına tıklıyoruz.

Adım 2:

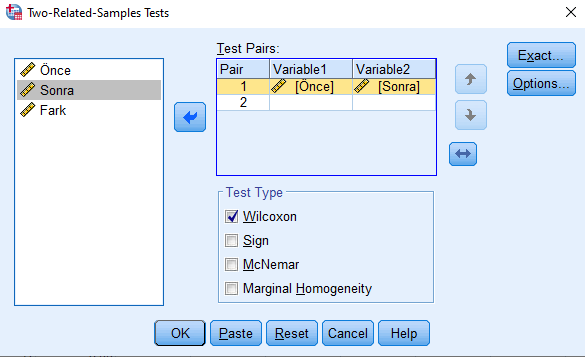
Sol taraftaki kutudan alıp sağdaki Test Pairs kısmında Variable 1’in altına önceki ölçüm değişkenimizi, Variable 2’nin altına ise sonraki ölçüm değişkenimizi taşıyoruz. Sırayla atmamız faydalı olur. Test Type kısmında da “Wilcoxon” işaretlenmiş olmalı. Bunları yaptıktan sonra pencere aşağıdaki resimdeki gibi görünmeli. Sonra OK’a basarak analiz sonuçlarını görebiliriz.

Wilcoxon Signed-Rank Test Yorumlama

Test sonucunun istatistiksel olarak anlamlı olmadığını öğrenmek için, Test Statistics tablosundaki Asymp. Sig. (2-tailed) değerine bakıyoruz. Bu değer bize Wilcoxon signed-rank testimizin p değerini verecektir.

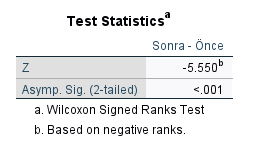
Örneğimizde p değeri 0.001’den küçük çıkmış, yani 0.05’ten küçük bir değer olduğu için anlamlı bir sonuç demek oluyor. Yani bu örnekte ilaç aldıktan sonra ve ilaç almadan önce kalp atış hızları arasında anlamlı bir fark var.

Peki kalp atış hızı ilaç almadan önce mi yoksa aldıktan sonra mı daha yüksek?

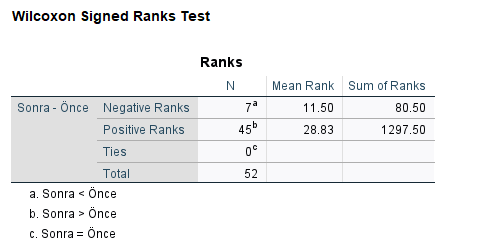
Bunu görmek için de, aynı sonuç sayfasındaki “Ranks” başlıklı tabloya bakmamız gerekiyor.

• Bu tablodaki Negative Ranks’in N sütununda karşılık geldiği sayı ilaç aldıktan sonra kalp atış hızı azalan kaç kişi olduğunu gösterir.
• Positive Ranks’in N sütununda karşılık geldiği sayı ilaç aldıktan sonra kalp atış hızı artan kaç kişi olduğunu gösterir.
• Ties bölümü de artış ya da azalış olmayan kişi sayısını gösterir.

Aşağıdaki tabloda, ilaç aldıktan sonra kalp atış hızı artan 45 kişi, azalan 7 kişi olduğunu görüyoruz. Hatırlarsak bir önceki tabloya göre p değeri 0.001’den küçüktü yani 0.05’in altında olduğu için önceki ve sonraki kalp atış hızı ölçümleri arasında anlamlı bir fark var demiştik. Sonuçları “Demek ki ilaç aldıktan sonra kalp atış hızı anlamlı bir şekilde artmıştır” diye yorumlayabiliriz.

Wilcoxon Signed-Rank Test Etki Büyüklüğü Bulma

Wilcoxon Signed-Rank Test sonucu, eğer anlamlı bir etki çıkarsa (p < 0.05), o zaman etki büyüklüğü değerini de yorumlamamız faydalı olacaktır. Wilcoxon Signed-Rank Test için etki büyüklüğü Z / √(n) formülüyle hesaplanabilir.

Yani, test sonuçlarında SPSS’te Test Statistics tablosunda yazan Z değerini, katılımcı sayısının kareköküne bölersek Wilcoxon Signed-Rank Test sonucundaki etki büyüklüğünü buluyoruz.

Bu örnekte Z değeri -5.550 ve katılımcı sayısı 52. Formülde yerlerine yerleştirirsek [-5.550 / √(52) = -0.77] şeklinde, etki büyüklüğünü -0.77 olarak buluyoruz.

Etki büyüklüğünün negatif ya da pozitif olması fark etmez, 0’a olan uzaklığı önemli. Etki büyüklüğü yorumlama için de şu değer aralıkları kullanılabilir:

Bizim örneğimizde etki büyüklüğü -0.77 çıktı. Bu değerin 0’a uzaklığı 0.50’den daha büyük olduğu için, bu örnekte çok büyük bir etki büyüklüğü olduğu sonucuna varabiliriz. Yani “ilacı aldıktan sonra kalp atış hızı çok büyük miktarda artmış” şeklinde bir yorum yapabiliriz.