
İçindekiler
Binary yani ikili lojistik regresyon, veri analizinde sıklıkla kullanılan güçlü bir istatistiksel araçtır. Bu yöntem, bir veya daha fazla bağımsız değişkenin ışığında, 2 sonuç kategorisi arasından hangisinin gerçekleşeceğini tahmin etmek için kullanılır. Bu blog yazısında, binary lojistik regresyonun temel prensiplerini ve SPSS kullanarak nasıl analiz gerçekleştirileceğini inceleyeceğiz.
Binary Lojistik Regresyon Nedir?
Binary (ikili) lojistik regresyon, bir adet kategorik bağımlı değişken ile bir veya daha fazla bağımsız değişken arasındaki ilişkiyi modellemek için kullanılan bir istatistiksel yöntemdir. Binary lojistik regresyon olabilmesi için bağımlı değişkenin, genellikle “evet” veya “hayır”, “başarı” veya “başarısızlık”, veya “0” veya “1” gibi sadece iki kategoriye sahip değerler alması gerekir. Bağımsız değişkenler her tür veri tipinde olabilir; ise ister kategorik ister sürekli veri tipinde olsun.
Eğer bağımlı değişken 3 veya daha fazla kategoriye sahip bir kategorik veri ise, binary lojistik regresyon yerine multinominal lojistik regresyon yapmamız gerekmektedir.
Binary lojistik regresyonun amacı, bağımsız değişkenlerin değerlerine dayanarak bağımlı değişkenin belirli bir kategoriye ait olma olasılığını tahmin etmektir. Lojistik regresyon modeli, bağımsız değişkenlerin lineer kombinasyonunu 0 ile 1 arasında bir olasılık skoruna dönüştürmek için lojistik fonksiyonu (veya S şeklindeki sigmoid fonksiyonu) kullanır. Model daha sonra belirlenen bir eşik olasılığına dayanarak gözlemleri iki kategoriye ayırır.
Binary lojistik regresyon, verilere dayanarak müşteri kaybını tahmin etme, risk faktörlerine bağlı olarak bir hastalığın gerçekleşme ihtimalini tahmin etme, bir müşterinin bankadan aldığı krediyi geri ödeyebilme ihtimalini belirleme gibi amaçlar için kullanılır. Bu gibi açıklayıcı değişkenlere dayanarak bir olayın meydana gelme olasılığını modelleme amacıyla tıp, ekonomi, sosyal bilimler ve pazarlama gibi çeşitli alanlarda yaygın olarak kullanılmaktadır.
Binary Lojistik Regresyon Varsayımları
Binary lojistik regresyon, oldukça güçlü bir regresyon analizi türüdür. Öyle ki binary lojistik regresyon yapabilmek için çok fazla varsayımın doğrulanması gerekmez. Örneğin bağımsız değişkenlerin kategorik, ordinal veya sürekli veri tipinde olması fark etmez hepsi geçerlidir. Yalnızca, bağımlı değişkenin 2 kategoriye sahip bir kategorik değişken olması şarttır. Bunun dışında, birden fazla sürekli veri tipinde bağımsız değişken varsa, bunların birbirleriyle çok yüksek korelasyon göstermemesi iyi olur, fakat bu olsa bile çok önemli bir sorun yaratmaz.
Binary lojistik regresyon yapabilmemiz için bağımlı değişkenin yalnızca 2 kategoriye sahip bir kategorik veri olması şarttır.
SPSS ile Binary Lojistik Regresyon Nasıl Yapılır?
SPSS’te binary lojistik regresyon analizi gerçekleştirmek gerektiğini aşağıda anlatıyorum. Bu sayfadaki örnekte, ihtiyacınız olabilecek bütün türlerde değişkenlere yer verdim. Sizin elinizde hangi tür veri olursa olsun, bu yazıyı sonuna kadar okursanız kendi regresyon analizinizi doğru gerçekleştirebilmek için başka kaynağa bakmaya ihtiyacınız olmayacak.
Bu sayfadaki örnekte, her katılımcı için, gerçekleşebilecek 2 sonuçtan hangisinin gerçekleşmeye daha yakın olduğunu binary lojistik regresyon analiziyle bulmaya çalışacağım.
Analize başlamadan önce, bu örnekte çalışacağım veri setini kısaca tanıtmak istiyorum. Bu, analizi nasıl yaptığımızı anlamanız için önemli.
Analizimde, bir kişinin Cinsiyet, Mutluluk, Medeni Durum, ve Ekonomik Durumuna göre, seçimde Evet oyu mu yoksa Hayır oyu mu vermeye daha yakın olduğunu tahmin etmeye çalışacağım.

Değişkenlerin kodlanması şu şekilde:
- Cinsiyet -> Kategorik veri (5 = Kadın; 6 = Erkek)
- Mutluluk -> Sürekli veri (1’den 7’ye kadar)
- Medeni durum -> Kategorik veri (0 = Bekar; 1 = Evli)
- Ekonomik durum -> Kategorik veri (1 = Fakir; 2 = Orta; 3 = Zengin)
Lojistik regresyon analizimizi yapmaya Analyze -> Regression -> Binary Logistic düğmelerine basarak başlıyoruz.
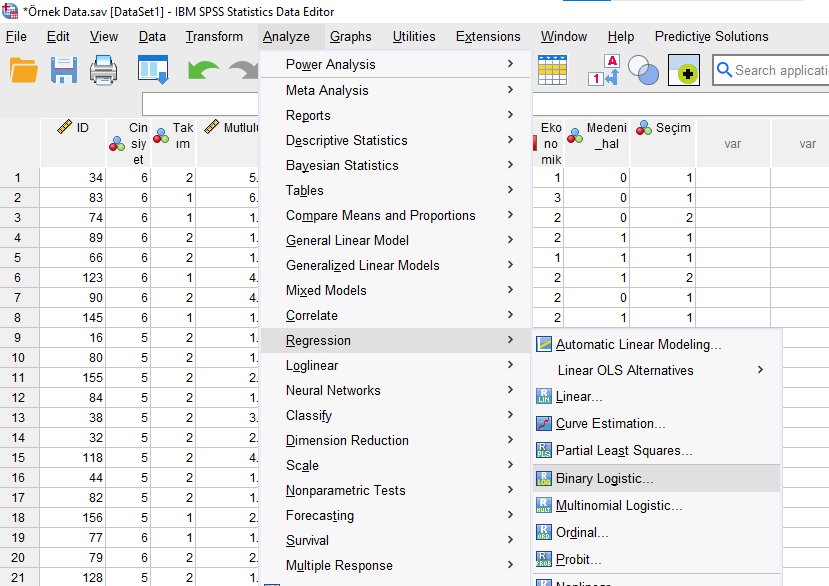
Bağımlı değişkenimizi Dependent kutusuna, bağımsız değişkenlerimizin hepsini Covariates kutusuna koyuyoruz. Hangi sırayla koyduğumuzun önemi yok.
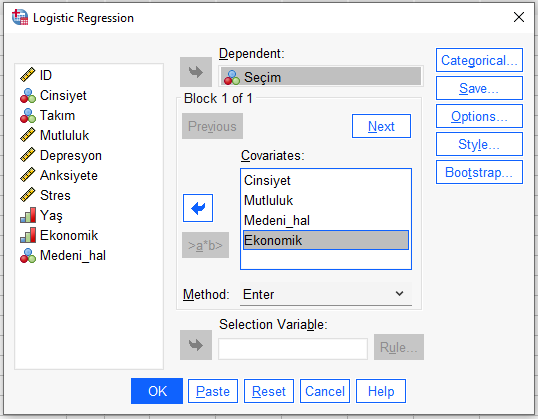
Categorical butonuna basıyoruz. SPSS o kadar da süper otomasyon bir program olmadığı için, kategorik verilerimizi 0 ile 1 olarak göstermesi için bizim ona burada talimat vermemiz gerekiyor. Yoksa analiz sonucunu düzgün göstermez.
Yukarıda veri setimizi hatırlarsak, Medeni Hal değişkeni Evli = 1, Bekar = 0 olarak kodlanmıştı. Bunu SPSS’e yeniden kodlatmaya gerek yok. Fakat Cinsiyet ve Ekonomik Durum değişkenleri 0 – 1 şeklinde kodlanmamıştı.
Bunları SPSS’in analiz sırasında 0 ve 1 şeklinde kodlamasını sağlamamız gerek. Bu yüzden bu iki değişkeni alıyorum ve Categorical Covariates kutusuna koyuyorum. Reference Category olarak First seçersek, bu kategorilerdeki en küçük sayısal değere sahip olan kategori, referans kategorisi olarak sayılır yani SPSS analiz sonucunda “0” olarak geçer. Diğer değişken 1 olarak geçer. Bunu SPSS tablo çıktılarını aldıktan sonra tekrar göstereceğim.
Medeni Hal değişkeni zaten en baştan 0 ve 1 olarak kodlanmış olduğu için bunu bu adımda ellemeye gerek yok. Eğer baştan 0 ve 1 olarak kodlanmamış olsaydı bunu da aşağıda kutuya atardık.
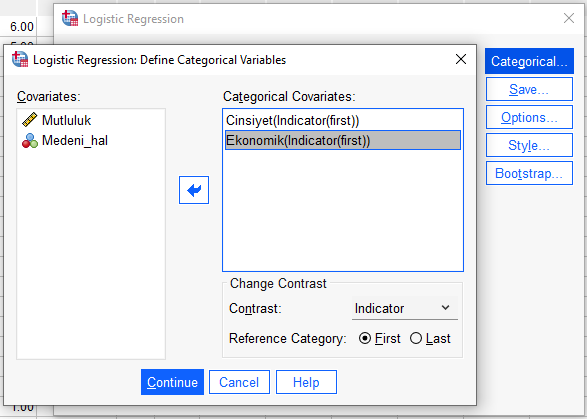
Daha sonra, Save’e basıyorum. Predicted Values kısmında, Probabilities ve Group Membership seçeneklerini işaretliyoruz.
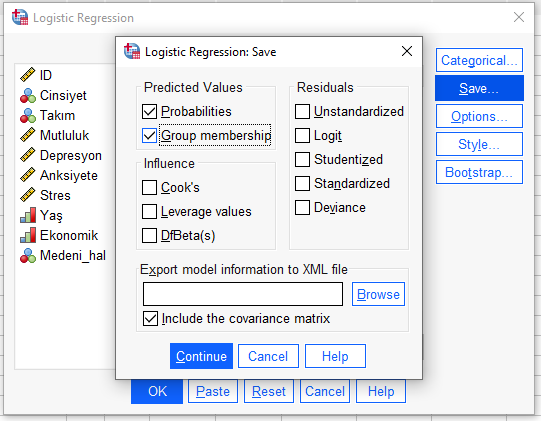
Options butonuna basıyoruz. “Hosmer-Lemeshow Goodness Of Fit” ve “CI For exp(B)” işaretliyoruz.
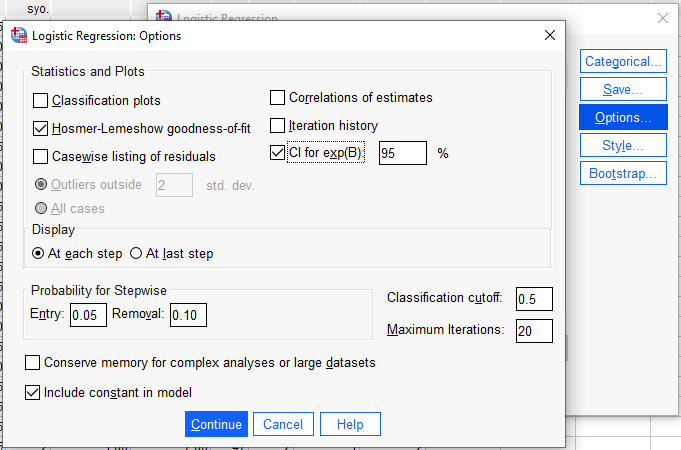
Artık sırasıyla Continue ve OK butonlarına basarsak SPSS bize binary lojistik regresyon analizi tablolarını sunacak.
Binary Lojistik Regresyon SPSS Tablo Yorumlama
Aşağıda, SPSS’in bize verdiği binary lojistik regresyon tablolarında hangi yerlere bakmak gerektiğini anlatıyorum. Binary lojistik regresyon analiz yorumlama yaparken büyük ihtimalle bunların dışında bir yere bakmanız gerekmeyecek.
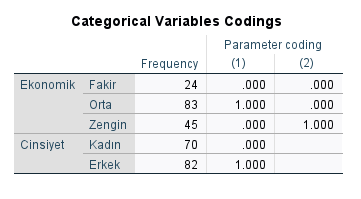
Öncelikle, hatırlarsanız demin SPSS’e Cinsiyet ve Ekonomik Durum kategorik değişkenlerimizi 0 ve 1 olarak kodlatmıştık. Bunu aşağıdaki “Categorical Variables Codings” başlıklı tabloda görebiliriz.
Cinsiyet olarak, artık Kadın = 0; Erkek = 1 şeklinde kodlanmış bulunuyor.
Ekonomik Durum olarak ise 2 farklı kodlama şekli görüyoruz çünkü bu değişken 3 kategoriye sahip. Fakir grubunu demin First seçerek referans değeri olarak belirlemiş olduğumuz için hep 0 değerinde. (Eğer Last seçmiş olsaydık Zengin kategorisi hep 0 değerinde olacaktı.) Bir kodlama şeklinde Fakir = 0; Orta = 1 sayılmış, diğer kodlama şeklinde Fakir = 0; Zengin = 1 sayılmış. Yani birinde Orta gelirli katılımcılar ile Fakir katılımcılar karşılaştırılıyor, diğerinde ise Zengin katılımcılar ile Fakir katılımcılar karşılaştırılıyor.
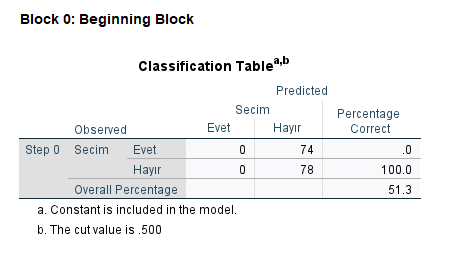
Block 0’daki “Classification Table” başlıklı tabloda, eğer hiçbir istatistiksel modelimiz olmasaydı, kimin hangi oyu vereceğini rastgele seçseydik, yüzde kaç oranında doğru bileceğimizi görüyoruz. Genelde %50’ye yakın bir değer çıkar burası. Çok da önemli değil bu tablo.
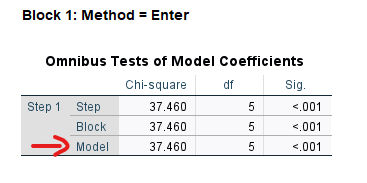
Block 1’den sonraki tablolar biraz daha önemli. Aşağıdaki tablodaki “Model” satırındaki Sig. değeri, yaptığımız binary lojistik regresyon analizinin istatistiksel olarak anlamlı bir p değeri yani sonuç verip vermediğini söylüyor. Eğer 0.05’ten küçük ise anlamlı demektir. Biz p < 0.001 bulduk, yani bu demek oluyor ki, kurduğumuz lojistik regresyon modeline göre bağımsız değişkenlerimizden en az 1 tanesi, bağımlı değişken olan Seçim’deki Evet veya Hayır verme ihtimalini etkiliyor.
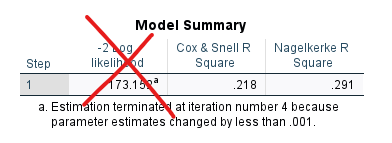
“Model Summary” tablosunda, modelimizin Seçim’deki Evet Hayır tercihini ne kadar etkilediği hakkında bir fikir sahibi olmamıza yardımcı olan değerler görüyoruz. İki tane R Square değeri görüyoruz. Bu değerler, doğrusal (lineer) regresyon modellerinde kullandığımız R Kare ve Düzeltilmiş R Kare değerlerinin bir analojisi olarak düşünülebilir. Ama hesaplanma yöntemleri farklıdır, o yüzden doğrusal regresyondaki R Kare değeriyle tam olarak aynı şey değildirler.
Doğrusal regresyonda R Kare (R Square) değeri, bağımlı değişkendeki değişkenliğin yüzde kaçının bağımsız değişkenlerle açıkladığını belirtiyordu. Mesela, eğer doğrusal regresyonda R Kare değerini 0.41 olarak bulursak, bu, o regresyon modelindeki bağımsız değişkenlerin bağımlı değişkendeki değişimin %41’ini açıkladığını gösteriyordu.
Fakat lojistik regresyondaki Cox & Snell R Square ve Nagelkerke R Square değerleri, bu şekilde yorumlanmamalıdır, çünkü hesaplanma biçimleri farklıdır. Ayrıca Cox & Snell R Square değeri nadir de olsa 1’den büyük olabilir. Nagelkerke R Square ise, Cox & Snell R Square değerinin 0 ile 1 arasında olacak şekilde modifiye edilmiş versiyonudur.
Eğer Psikoloji öğrencisiyseniz hocanız muhtemelen bu R Square değerlerine bakıp lojistik regresyon modelinizin bağımlı değişkendeki değişimin yüzde kaçını açıkladığını söylemenizi bekleyecektir. Yani aşağıdaki tabloyu şöyle yorumlamanızı isteyecektir: “Cox & Snell R Square değerine göre modelimiz Seçim tercihindeki değişimin %21.8’ini açıklıyor” veya “Nagelkerke R Square değerine göre modelimiz Seçim tercihindeki değişimin %29.1’ini açıklıyor”. Bu aslında matematiksel olarak yanlış, fakat hocanız eğer böyle diyorsa hocanızın suyuna gitmekte fayda var.
“Hosmer and Lemeshow Test” tablosunda, Sig. sütununda 0.05’ten büyük bir p değeri çıkmasını istiyoruz. Eğer böyle ise lojistik regresyon modelimiz verimize iyi uyum sağlıyor demektir.
Hosmer-Lemeshow testi, bir lojistik regresyon modelinin uyum iyiliğini değerlendirmek için kullanılan bir istatistiksel testtir. SPSS’te, Hosmer-Lemeshow testi sonucu bulduğumuz p değeri, testin anlamlılık düzeyini gösterir. 0.05’ten küçük bir p-değeri lojistik regresyon modelinin veriye iyi uymayabileceğini gösterebilirken, 0.05’ten büyük bir p-değeri modelin veriye iyi uyum sağladığını işaret eder.

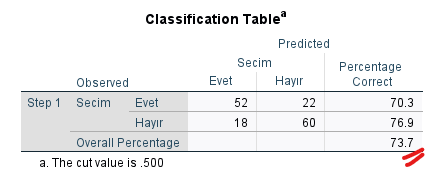
“Classification Table” tablosunda, SPSS’in oluşturduğu lojistik regresyon modelinin, katılımcıların yüzde kaçının Seçim’deki Evet veya Hayır tercihini doğru bildiğini gösteren verileri görebiliriz. “Observed” bölümü gerçek değeri, “Predicted” bölümü modelin tahmin ettiği değeri gösterir.
Bu örnekte, SPSS Seçim’de Evet oyu veren 74 kişinin 52’sinin Evet oyu vereceğini doğru tahmin etmiş, fakat 22’sinin Hayır oyu vereceğini tahmin etmiş (yani yanlış tahmin etmiş). SPSS’in tahminlerinin %70.3’ü doğruymuş.
Benzer şekilde, SPSS Seçim’de Hayır oyu veren 78 kişinin 60’ının Hayır oyu vereceğini doğru tahmin etmiş, fakat 18’inin Evet oyu vereceğini tahmin etmiş (yani yanlış tahmin etmiş). SPSS’in tahminlerinin %76.9’u doğruymuş.
Bütün veriyi topluca ele alırsak, SPSS’in kurduğu lojistik regresyon modeline göre yaptığı tahminlerin %73.7’si doğruymuş. Baştaki, rastgele tahmin yaparsak yüzde kaçını doğru bileceğimizi söyleyen modelde tahminlerimizin %51.3’ü doğru çıkıyordu. Lojistik regresyon analizi sonucu kurduğumuz modelde, doğru tahmin oranımız %51.3’ten %73.7’ye çıktı ve bu istatistiksel olarak anlamlı bir yükseliş (çünkü yukarıda Model’in p değerini 0.05’ten küçük bulmuştuk).
“Variables in the Equation” tablosu en önemli tablo. Burayı doğru yorumlamak çok önemli, hangi değişkenlerin sonucu nasıl etkilediğini bu tabloya bakarak öğrenebiliyoruz. Yorumlamak biraz uzun ama çok zor değil.
Sırayla satır satır yorumlayarak gideceğim.
Öncelikle hatırlayalım ki Seçim tercihleri, bizim verimizde 1 = Evet; 2 = Hayır olarak kodlanmıştı.
Cinsiyet
Cinsiyet değişkeninin Sig. yani p değeri 0.001’den küçük çıkmış. Yani istatistiksel olarak anlamlı bir sonuca işaret ediyor. Cinsiyet kategorik bir değişken. Yukarıdan hatırlarsak Kadın = 0; Erkek = 1 olarak yeniden kodlamıştık.
B değeri pozitif. B değeri sadece doğrusal bir fonksiyonda işe yarayan bir katsayıdır. Fakat lojistik regresyon doğrusal bir fonksiyon değil. Bu yüzden B değerini Exp(B) diye başka bir katsayıya çevirip onu yorumlamak gerekiyor. O yüzden biz B yerine Exp(B) değerine bakıp yorumlama yapacağız. Cinsiyet’in Exp(B) değeri 8.695’miş.
Exp(B), bir lojistik regresyon modelinin B katsayısının üstel fonksiyonunu ifade eder. Bu, bir birimlik değişikliğin olasılık oranındaki (Odds Ratio) etkisini temsil eder. Bu yüzden Exp(B) değeri için Odds Ratio terimi de kullanılmaktadır.
Cinsiyet ve Seçim tercihini hangi sayılarla kodladığımızı hatırlarsak, şöyle bir sonuca varabiliriz: “Kadın yerine Erkek olmak, seçimde Evet yerine Hayır oyu verme ihtimalini 8.695 kat arttırıyor. Yani Erkek olmak Hayır oyu verme ihtimalini %869.5 arttırıyor.”
B değeri pozitif ise Exp(B) değeri her zaman 1’den büyük olur, B değeri negatif ise Exp(B) değeri her zaman 1’den küçük olur.
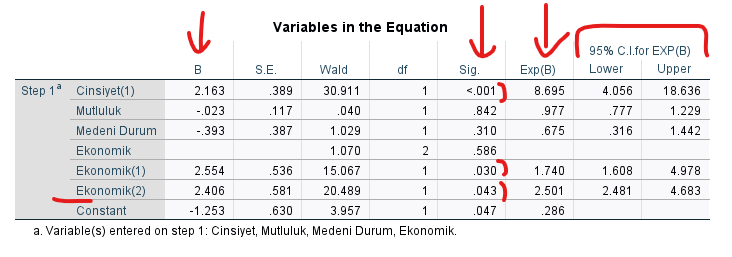
Tablonun en sağında Exp(B) değeri için %95 güven aralığını belirten sayılar var. Soldaki sütun o değişken için olabilecek en düşük Exp(B) değerini, sağdaki sütun da en yüksek Exp(B) değerini gösteriyor. Eğer Sig. sütunundaki değer 0.05’ten küçük ise, “%95 CI for Exp(B)” bölümündeki değerlerin ya ikisi de 0’dan küçük olur, ya da ikisi de 1’den büyük olur. Değerlerin arasına hiçbir zaman 0 girmez.
Mutluluk
Mutluluk değişkeninin Sig. yani p değeri 0.842 çıkmış. Yani sonuç istatistiksel olarak anlamlı değil. Bu yüzden normalde bu değişken için tabloyu daha fazla okumaya gerek yok.
Fakat örnek göstermek açısından, eğer istatistiksel olarak anlamlı bir p değeri çıksaydı nasıl olurdu yorumlayalım.
(Hatırlarsak başta Seçim oy tercihi Evet = 1; Hayır = 2 kodlamıştık.)
Yine Exp(B) değerine bakıyoruz. Exp(B) değeri 0.977 çıkmış, B değeri de negatif. Bu şu anlama geliyor: Mutluluk puanı arttıkça, Hayır oyu verme oranı azalıyor. Sayısal olarak detaylıca şöyle yorumlayabiliriz: “Mutluluk’ta eğer 1 puanlık artış meydana geliyor ise, bir katılımcının Evet yerine Hayır oyu verme ihtimali, ilk baştaki ihtimalin %97.7’si kadardır.”
Mutluluk’ta eğer 2 puanlık artış meydana geliyorsa Hayır oyu verme ihtimali, en baştaki ihtimalin %97.7’sinin %97.7’si kadar oluyor yani en baştaki ihtimalin %94.1’i kadar oluyor.
1 – 0.977 = 0.023 yapar diye bir hesap yaparak aynı sonucu farklı kelimelerle de anlatabiliriz: “Mutluluk puanındaki her 1 puanlık artış, bir kişinin seçimde Hayır oyu verme ihtimalini önceki ihtimale göre %2.3 azaltıyor”.

Medeni Durum
Mutluluk değişkeninin Sig. yani p değeri 0.310 çıkmış. Yani sonuç istatistiksel olarak anlamlı değil. Bu yüzden normalde bu değişken için tabloyu daha fazla okumaya gerek yok.
Fakat örnek göstermek açısından, eğer istatistiksel olarak anlamlı bir p değeri çıksaydı nasıl olurdu yorumlayalım.
Medeni Durum en başta 0 = Bekar; 1 = Evli olarak kodlanmıştı. Seçim de 1 = Evet; 2 = Hayır olarak kodlanmıştı.
Exp(B) değeri 0.675 ve B değeri negatif. Şöyle yorumluyoruz: “Bekar yerine Evli olmak, seçimde Hayır oyu verme ihtimalini baştaki ihtimalin sadece %67.5’u kadar yapıyor.”
1 – 0.675 = 0.325
Başka bir deyişle: “Evli olmak, Hayır oyu verme ihtimalini %32.5 oranında azaltıyor.”

Ekonomik Durum
Ekonomik Durum, 3 farklı değer alabilen bir kategorik değişken olduğundan dolayı (Fakir – Orta – Zengin) Fakir’i referans kategorisi olarak ayarlayıp Orta ile ve Zengin ile karşılaştırdığımız 2 tane farklı model oluşturmamız gerekmişti.
1. modele bakarsak, Sig. yani p değeri 0.030 yani istatistiksel olarak anlamlı. 1. modelde Fakir = 0; Orta = 1 diye kodlamıştık. Exp(B) değerine bakarsak, diyebiliriz ki “Fakir yerine Orta ekonomik durumda olmak, seçimde Hayır oyu verme ihtimalini %74 arttırarak %174’e çıkartıyor”.
2. modele bakarsak, Sig. yani p değeri 0.043 yani istatistiksel olarak anlamlı. 2. modelde Fakir = 0; Zengin = 1 diye kodlamıştık. Exp(B) değerine bakarsak, diyebiliriz ki “Fakir yerine Zengin olmak, seçimde Hayır oyu verme ihtimalini %150.1 arttırarak %250.1’e çıkartıyor”.
Not: Burada maalesef Orta ekonomik durumdan Zengin ekonomik duruma geçmek Hayır oyu verme ihtimalini ne kadar arttırıyor direkt olarak göremiyoruz. Bunu görebilmek için Orta’yı referans kategorisi olarak ayarlayıp yeniden aynı lojistik regresyon analizini yapmalıyız. O zaman görürüz.

Sonuç olarak, diyebiliriz ki “Cinsiyet Erkek olunca ve Ekonomik durum iyiye gittikçe seçimde Hayır oyu verme ihtimali istatistiksel olarak anlamlı bir şekilde artıyor.” Ne kadar arttığını da yukarıda söyledik.
Binary lojistik regresyon SPSS tablosu yorumlama kısmı bu kadardı. Son olarak, SPSS veri setimizde bir şeyi daha göstereceğim. Analizi ilk yaparken “Save”den Predicted Values kısmındaki Probabilities ve Group Membership seçeneklerini işaretlemiştik. Bu, SPSS veri setimizde en sağdaki sütunun sağında iki yeni sütunda iki yeni değişken oluşmasına sebep oldu: PRE_1 ve PGR_1. Bu iki değişkene bakarak, SPSS’in, veri setimizdeki her katılımcı için bir değer hesaplayıp o değere göre o katılımcının hangi grupta olduğunu (hangi oyu verdiğini) tahmin ediyor.
- PRE_1 = Predicted Value yani Tahmini Değer
- PGR_1 = Predicted Group Membership yani Beklenen Grup
Her satırda, SPSS o katılımcının Cinsiyet, Mutluluk, Medeni Durum ve Ekonomik Durum değerlerine göre bir tahmini değer hesaplıyor. O değere göre de o katılımcının Evet mi Hayır mı oy vermesi gerektiğini tahmin ediyor (Evet = 1; Hayır = 2).
Predicted Value (PRE_1) değeri 0.50’den küçükse Predicted Group (PGR_1) otomatikman 1 olur; Predicted Value (PRE_1) değeri 0.50’den büyükse Predicted Group (PGR_1) otomatikman 2 olur.

Aşağıya deminki görselin biraz daha büyük halini koydum.
Seçim sütununda her katılımcının gerçekte verdiği oy görünüyor. PGR_1 sütununda ise SPSS’in o katılımcının hangi oyu verdiğini tahmin ettiği görünüyor.
Örneğin 1. satırda katılımcı Evet oyu vermiş. SPSS de o kişinin incelediğimiz dört bağımsız değişkeninin durumuna bakarak o kişinin Evet oyu verdiğini tahmin etmiş. Doğru tahmin etmiş.
2. satırda katılımcı Hayır oyu vermiş. SPSS o kişinin incelediğimiz dört bağımsız değişkeninin durumuna bakarak o kişinin Evet oyu verdiğini tahmin etmiş. Yanlış tahmin etmiş.
Örneğin 3. satırda katılımcı Hayır oyu vermiş. SPSS de o kişinin incelediğimiz dört bağımsız değişkeninin durumuna bakarak o kişinin Hayır oyu verdiğini tahmin etmiş. Doğru tahmin etmiş.
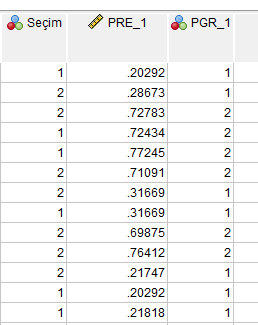
Yukarıda SPSS’in verdiği ilk sonuç tablolarından hatırlarsak, SPSS’in lojistik regresyon modelinin doğru tahmin etme oranı %73.7’ydi. Bu şekilde, verimizdeki herkes için SPSS’in yaptığı tahminlerin doğruluğunun oranına bakarsak, bütün katılımcılar için toplam tahminlerin %73.7’sinin doğru olduğunu anlıyoruz.

Binary lojistik regresyon SPSS analizi ve yorumlaması bu kadardı. Artık analizimizi raporlama işlemini yapabiliriz. Yazıyı baştan sona okuduysanız, analiz yapma ve yorumlama kısmında hiçbir sorun yaşamıyor olmanız lazım.
Eğer buradaki gibi 2 değerli değil de 3 veya daha fazla değer alabilen bir bağımlı değişkenin ihtimallerinin gerçekleşme oranını merak ediyorsanız bunun için Multinominal Lojistik Regresyon (Multinomial Logistic Regression) yapmanız gerekmekte. Bunun için de yazdığım diğer yazıyı okuyabilirsiniz. Şimdilik görüşmek üzere.






Bir yanıt bırakın