
İçindekiler
- 1 İki Yönlü ANOVA Nedir?
- 2 İki Yönlü ANOVA Varsayımları Nelerdir?
- 3 SPSS ile İki Yönlü ANOVA Varsayımları Nasıl Test Edilir?
- 4 SPSS ile İki Yönlü ANOVA Nasıl Yapılır?
- 5 İki Yönlü ANOVA Tablo Yorumlama
- 6 Post Hoc Analizi
- 7 Basit Temel Etki Analizi (Simple Main Effects = SME Analysis)
- 8 İki Yönlü ANOVA Etki Büyüklüğü Yorumlama
- 9 İki Yönlü ANOVA Sonucu Raporlama (APA)
İki Yönlü ANOVA, istatistiksel bir analiz yöntemidir ve değişkenlikleri etkileyen iki farklı faktör arasındaki ilişkiyi incelemek için kullanılır. Bu blog yazısında, İki Yönlü ANOVA’nın ne olduğunu, varsayımlarını ve SPSS programıyla nasıl gerçekleştirilebileceğini öğreneceksiniz. İki Yönlü ANOVA’nın genel bir bakışını sunmaya başlayarak, bu analizi kullanarak elde edilen sonuçları yorumlamada daha bilinçli olmanıza yardımcı olmayı amaçlıyoruz.
Doğrudan ANOVA Yapma Adımlarına Geçmek İçin TIKLAYIN
İki Yönlü ANOVA Nedir?
İki yönlü ANOVA (Varyans Analizi) istatistiksel bir yöntemdir ve iki tane faktörün (yani iki farklı bağımsız değişkenin) bir adet bağımlı değişken üzerindeki birlikte etkisini incelemek için kullanılır. Bu yöntem, gruplar arasındaki farkların ve faktörlerin etkileşimlerinin istatistiksel olarak anlamlı olup olmadığını belirlemek için kullanılır.
Bu yöntem, iki bağımsız grup arasındaki farkları belirlemek için tek yönlü ANOVA’dan farklıdır. İki yönlü ANOVA, iki faktörün etkisini aynı anda değerlendirir. Yani bağımlı değişkene hem birinci faktörün kendi başına etkisini, hem ikinci faktörün kendi başına etkisini, hem de iki faktörün birlikte etkisini değerlendirmeye yarar.
Örnek
Bir örnek vermek gerekirse, bir araştırmacı bir ilacın etkisini incelemek istediğinde, ilacın farklı dozlarının (birincil faktör) ve farklı cinsiyetlerin (ikincil faktör) etkisini değerlendirmek için iki yönlü ANOVA kullanabilir. İki faktörün etkileşimini analiz etmek, ilacın farklı dozlarının kadınlar ve erkekler üzerindeki etkisinin farklı olup olmadığını belirlemek için önemlidir.
İki Yönlü ANOVA Varsayımları Nelerdir?
İki Yönlü ANOVA, istatistiksel analizlerde kullanılan bir yöntemdir. Ancak, bu yöntemi uygulamadan önce bazı varsayımların sağlanması gerekmektedir. Bu varsayımlar, güvenilir sonuçlar elde edebilmek için oldukça önemlidir. İki Yönlü ANOVA’nın kullanılabilmesi için aşağıdaki varsayımların yerine getirilmesi gerekmektedir.
1. Bağımsızlık Varsayımı:
Bu varsayım, gözlemler arasında birbirlerinden bağımsızlık olduğunu ifade eder. Yani, ölçümler arasında herhangi bir ilişki veya etkileşim olmamalıdır. Örneğin, bir deney sırasında aynı katılımcı üzerinde yapılan ölçümler birbirinden bağımsız olmalıdır.
2. Normallik Varsayımı:
Bu varsayım, verilerin normal dağılıma uyması gerektiğini ifade eder. Normal dağılım, verinin ortalamasının merkezlenmiş olduğu ve simetrik bir şekilde dağıldığı bir durumu ifade eder. Bu varsayımın sağlanmaması durumunda, sonuçlarda yanlılık oluşabilir.
3. Varyans Homojenliği Varsayımı:
Bu varsayım, gruplar arasındaki varyansların eşit olması gerektiğini ifade eder. Yani, gruplar arasında farklılık olabilir, ancak bu farklılıkların varyanslarının birbirine yakın olması gerekmektedir. Varyans homojenliği varsayımının sağlanmaması durumunda, sonuçlar güvenilir olmayabilir.
| Varsayım | Sağlanmalı mı? |
|---|---|
| Bağımsızlık | Evet |
| Normallik | Evet |
| Varyans Homojenliği | Evet |
İki Yönlü ANOVA analizi yapmadan önce yukarıdaki varsayımların sağlandığından emin olmalısınız. Eğer bu varsayımlar sağlanmıyorsa, ANOVA yerine Kruskal-Wallis testi gibi daha uygun istatistiksel analiz yöntemlerini kullanmanız gerekebilir.
SPSS ile İki Yönlü ANOVA Varsayımları Nasıl Test Edilir?
1) Gözlemler birbirinden bağımsız olmalıdır.
Bu varsayım, “aynı kişi, aynı değişken için farklı zamanlarda 2 kere ölçülmemiş olmalıdır” anlamına gelmektedir. Yani, deneydeki her katılımcı, yalnızca bir kere ölçülmüş olmalıdır.
2) Bağımlı değişkenin skorları “normal dağılım”a sahip olmalıdır.
Eğer normal dağılım hakkında aklınızda soru işareti varsa, bu sayfaya devam etmeden önce sitemizdeki Normal Dağılımı Test Etmek başlıklı yazımıza bakıp bu sayfayı okumaya ondan sonra devam etmenizi öneririz.
İki yönlü ANOVA testi için normallik varsayımını SPSS programında test etmemiz gerekiyor. Açıklamaları ve altlarındaki resimleri takip edebilirsiniz.
Normallik Varsayımı Adım 1:
İlk önce SPSS’te Analyze -> Descriptive Statistics -> Explore butonlarına basıyoruz.
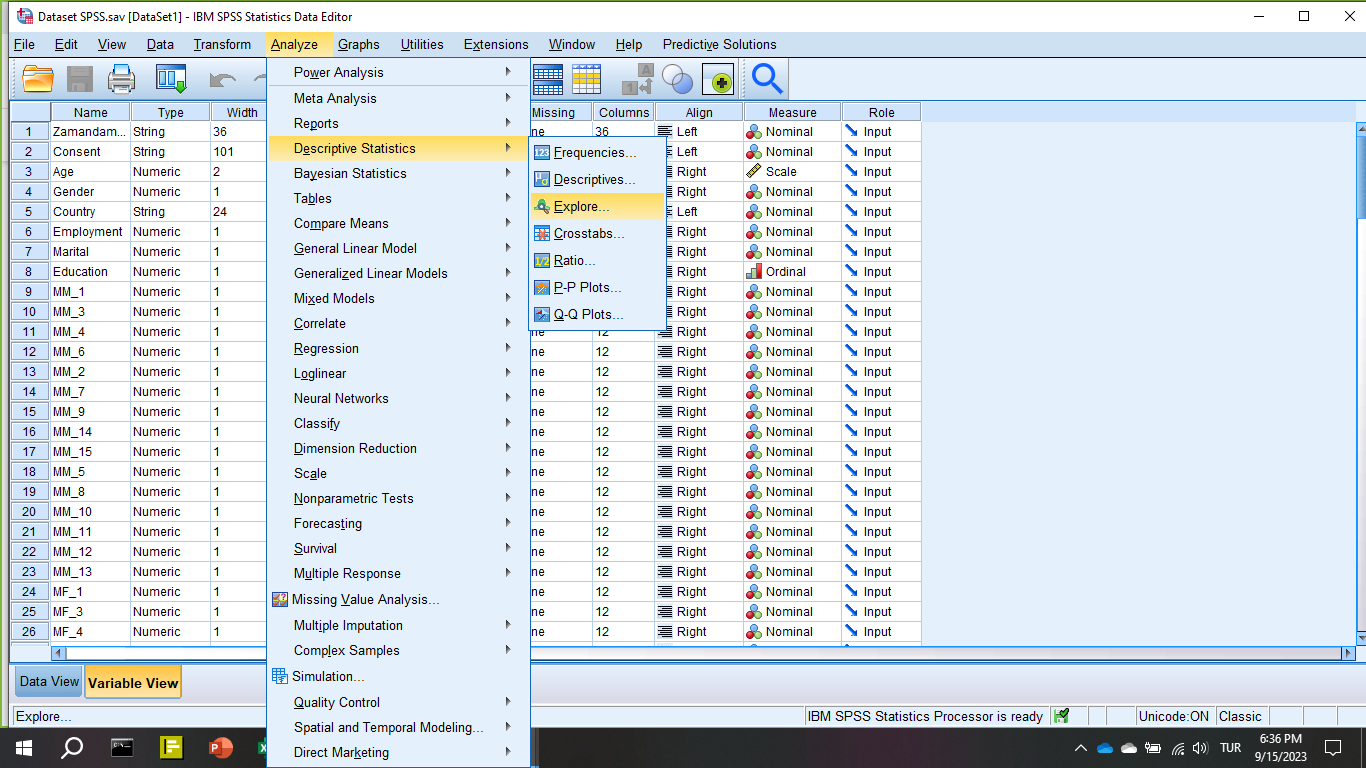
Normallik Varsayımı Adım 2:
Açılan yeni pencerede soldaki bölümden bağımlı değişkenimizi bulup sağ taraftaki Dependent List bölümüne atıyoruz. Sonra Plots butonuna basıyoruz.
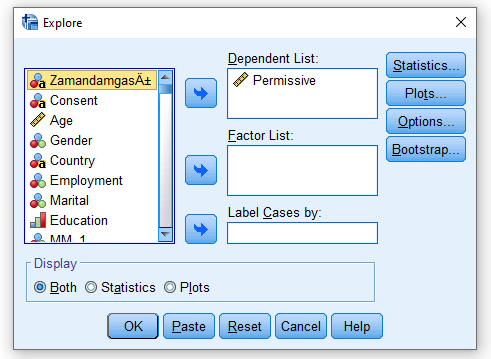
Normallik Varsayımı Adım 3:
Aşağıdaki resimde görüldüğü gibi, “Histogram” ve “Normality plots with tests” seçeneklerini işaretliyoruz. Continue’ya basıyoruz. Sonra OK tuşuna basıyoruz.
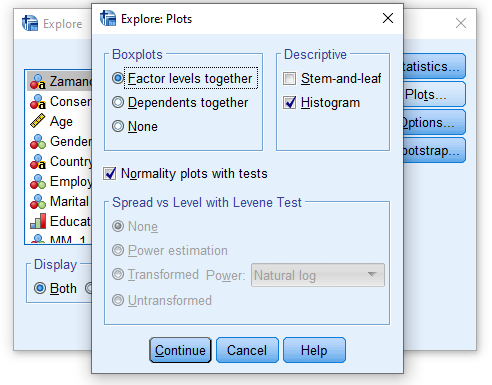
Normallik Varsayımı Adım 4:
SPSS yeni bir pencerede bize sonucu gösterecektir. Bu pencerenin adına Output deniyor. Output penceresinde “Tests of Normality” tablosuna bakmamız gerekiyor. Burada, Kolmogorov-Smirnov kısmındaki Sig. değerine veya Shapiro-Wilk kısmındaki Sig. değerine bakıyoruz. Bu değerler bize p değerini verir. Hangi kısımdaki değere baktığımız önemli. Eğer hangi kısımdaki değere bakacağınızdan emin değilseniz Normal Dağılımı Test Etmek konulu yazımıza bakabilirsiniz. Eğer Sig. değeri (yani p değeri) 0.05 değerinden büyük ise, normallik varsayımı doğrulanmış diyebiliyoruz.

SPSS ile İki Yönlü ANOVA Nasıl Yapılır?
Yukarıdaki adımların hepsini yapıp varsayımları başarıyla doğruladıktan sonra, artık ANOVA analizini yapma aşamasına geçebiliriz.
Burada yapacağımız örnekte, deneyimizdeki katılımcıları 2 farklı şekilde gruplandırıyoruz.
- Cinsiyet (erkek-kadın-diğer)
- Tuttuğu takım (Galatasaray-Fenerbahçe)
Bu katılımcılar arasında, katılımcının cinsiyetinin ve tuttuğu takımın o kişinin komiklik skoruna nasıl etki ettiğini inceleyeceğiz. Hazırsanız analizi yapmaya başlayalım.
Adım 1:
Öncelikle, SPSS’te Analyze -> General Linear Model -> Univariate butonlarına tıklıyoruz.
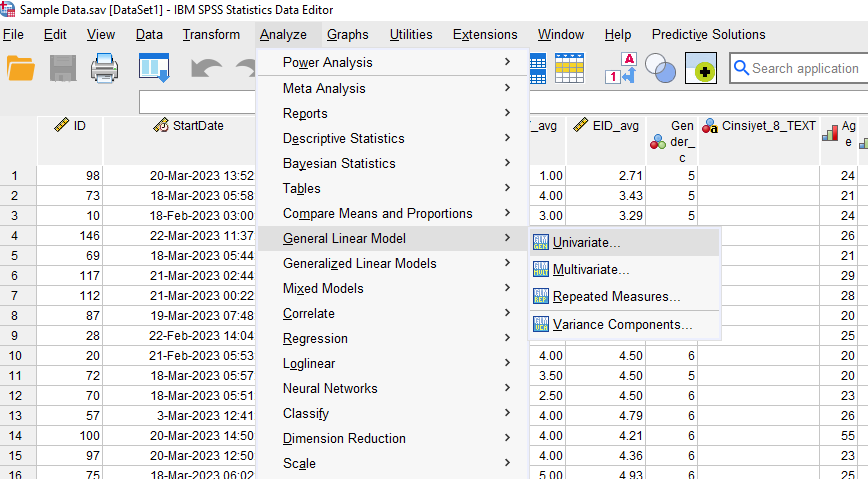
Adım 2:
Bağımsız değişkenimizi (Cinsiyet ve Takım) soldaki kutudan alıp sağdaki “Fixed Factors” kutusuna yerleştiriyoruz.
Bağımlı değişkenlerimizi (komiklik) soldaki kutudan alıp sağdaki “Dependent Variable” kutusuna yerleştiriyoruz.
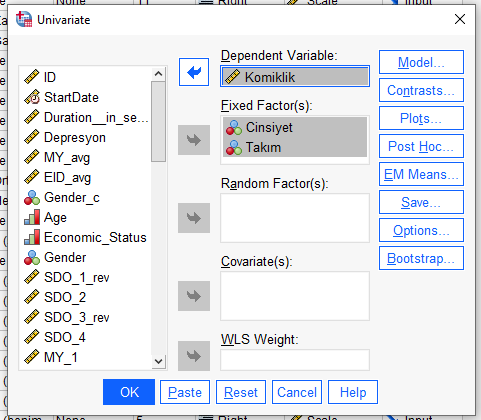
Adım 3:
Aynı “Univariate” penceresinde, “Options” butonuna basıyoruz. Açılan pencerede, aşağıdaki resimde görünen seçenekleri işaretliyoruz. Sonra “Continue” tuşuna basıyoruz.
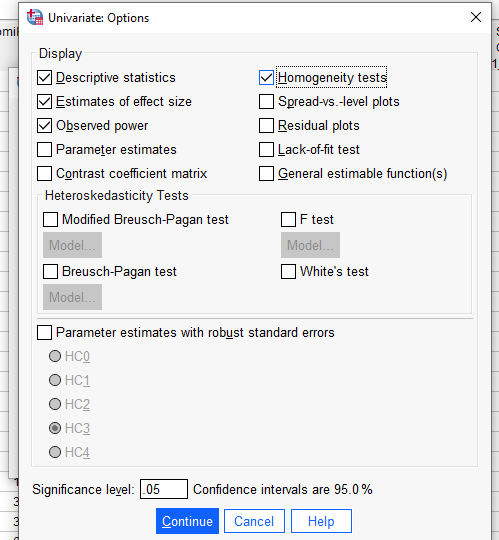
Adım 4:
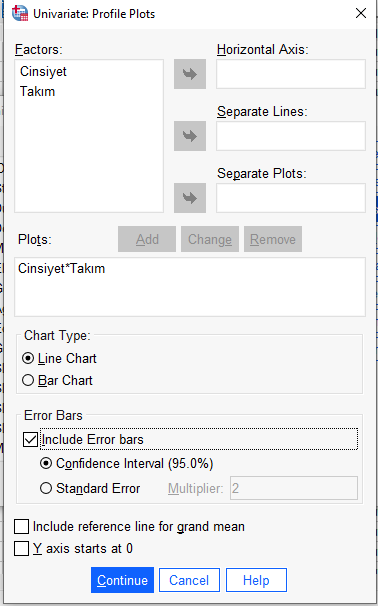
Yine deminki “Univariate” penceresinde, “Plots” butonuna basıyoruz. Aşağıdaki gibi bir pencere açılacak.
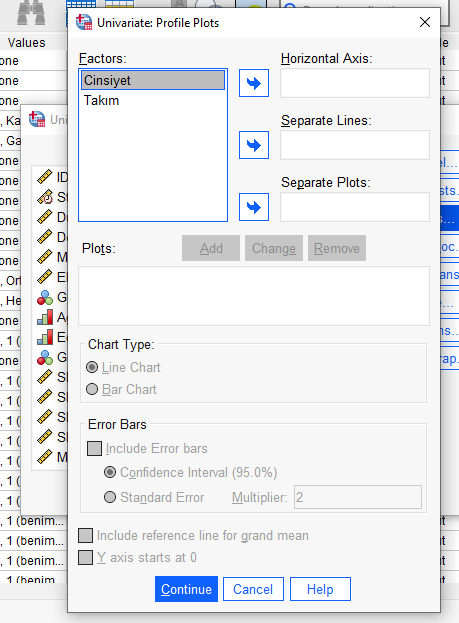
İki bağımsız değişkeni aşağıdaki gibi farklı kutulara alıyoruz. Daha sonra “Add” butonuna basacağız.
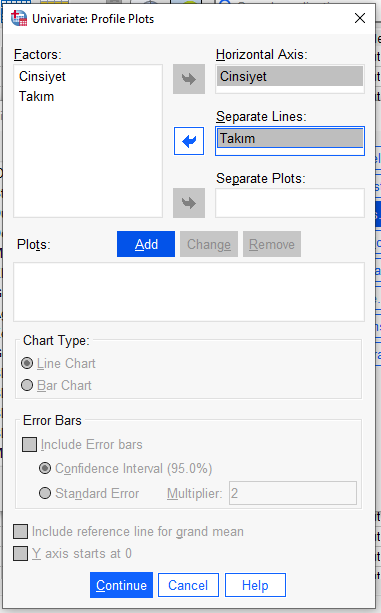
“Add”e bastıktan sonra, pencere aşağıdaki gibi görünecek. Resimde seçili olanları seçip “Continue”ya basıyoruz.
İki Yönlü ANOVA Tablo Yorumlama
Yukarıdaki işlemleri yapıp SPSS’te iki yönlü ANOVA analizimizi uyguladıktan sonra, karşımıza çeşitli tablolar ve grafikler gelecek. Bunların nasıl yorumlanacağına beraber bakalım.
Adım 1: Levene’s Test
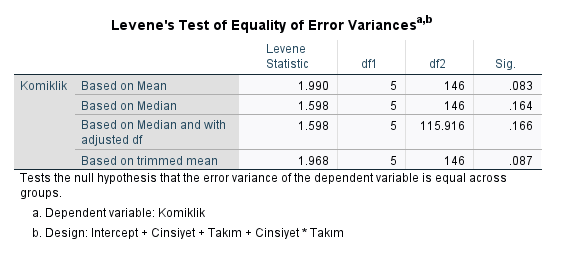
Öncelikle, Levene’s Test ile, grupların (cinsiyetlerin) puanları arasındaki varyansların homojen (yani birbirine benzer dağılıma sahip) olup olmadığına bakmamız gerekiyor. Buna, Levene’s Test tablosundan bakıyoruz.
Aşağıdaki tabloda, “Based on Mean” satırındaki “Sig.” değeri 0.05’ten büyük olmalı. Eğer büyük ise, ANOVA yorumlamaya normal bir şekilde devam edebiliriz. Bu örnekte, 0.083 çıktı yani 0.05’ten büyük. O zaman, ANOVA yapmaya sorunsuz olarak devam edebiliriz.
Eğer Levene’s Test sonucu p değeri 0.05’ten küçük çıksaydı, bir tane iki yönlü ANOVA yapmak yerine, her bağımsız değişken için ayrı ayrı olarak tek yönlü ANOVA’nın alternatifi olan non-parametrik testler olan Welch ya da Brown-Forsythe testlerinden bir tanesini yapmamız gerekecekti.
Adım 2: ANOVA p değeri yorumlama
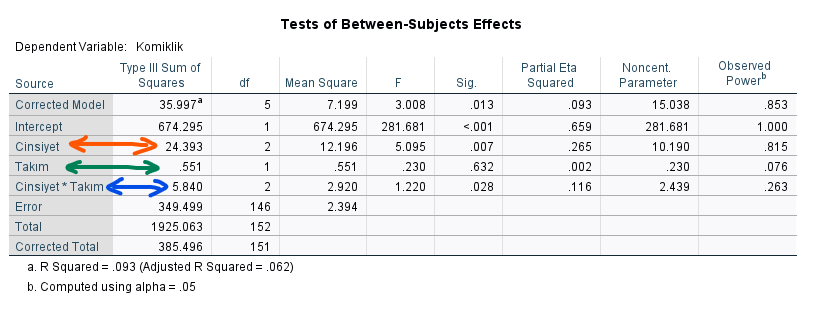
İki yönlü ANOVA sonucunu değerlendirirken, “Tests of Between-Subjects Effects” başlıklı tabloda üç satıra bakmamız gerekiyor.
Turuncu satırda, Cinsiyet’in tek başına komiklik skoruna etkisini görebiliriz. Bu örnekte “Sig.” yani p değeri 0.007 çıkmış. Bu p değeri 0.05’ten küçük olduğu için, “katılımcının hangi cinsiyette olduğu, komiklik skorunu anlamlı bir şekilde etkiliyor” diye yorumlayabiliriz. Bizim deneyimizde üç cinsiyet vardı. Hangi cinsiyetler arasında anlamlı bir skor farkı olduğunu görmek için, bir sonraki adımda post hoc analizi yapmamız gerekecek.
Yeşil satırda, Takım’ın tek başına komiklik skoruna etkisini görebiliriz. Bu örnekte “Sig.” yani p değeri 0.632 çıkmış. Bu p değeri 0.05’ten büyük olduğu için, “katılımcının hangi takımı tuttuğu, komiklik skorunu anlamlı bir şekilde etkilemiyor” diye yorumlayabiliriz.
Son olarak, iki yönlü ANOVA’nın tek yönlü ANOVA’dan en büyük farkı olan, mavi satıra bakalım. Bu satır, Cinsiyet ve Takım değişkenlerinin komiklik skoruna birlikte olan etkisine bakıyor. Bu örnekte “Sig.” yani p değeri 0.028 çıkmış. Bu p değeri 0.05’ten küçük. Bu durumu, “Cinsiyet ve Takım birlikte göz önüne alındığında, komiklik skoruna anlamlı bir etki var” olarak yorumlayabiliriz. Nasıl bir etki olduğunu öğrenmek için, post hoc testinin dışında basit temel etki analizi adlı bir analizi de yapmamız gerekecek.
Post Hoc Analizi
Herhangi bir tür ANOVA yaparken, eğer bir bağımsız değişken 2’den fazla gruba sahipse ve o değişkenin bağımlı değişken üzerindeki tek başına etkisini araştırmak istiyorsak, bir post hoc testi yapmalıyız.
Bizim örneğimizde, Cinsiyet değişkeni, erkek-kadın-diğer olarak üç farklı değer alabiliyordu. Ve ANOVA analizi sonucu cinsiyetin komiklik skoru üzerinde anlamlı bir etkisi olduğu sonucunu bulmuştuk. Hangi cinsiyetlerin komiklik skorları arasında anlamlı bir fark olduğunu bulmak için post hoc testi yapacağız.
Post hoc analizi yapmak için, SPSS’te yeniden Analyze -> General Linear Model -> Univariate tuşlarına basıp Univariate penceresinde, “Post Hoc” butonuna basmamız gerekiyor.

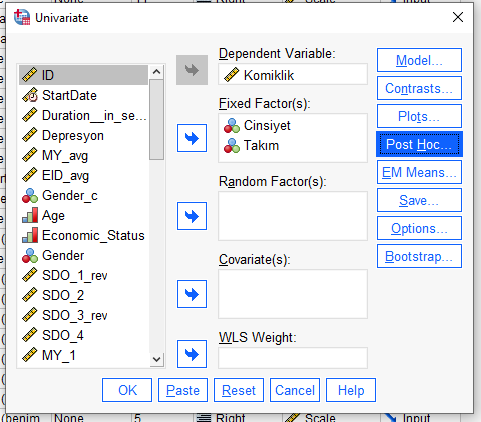
Açılan pencerede, sol kutudan Cinsiyet değişkenini alıyoruz ve sağdaki kutuya atıyoruz. Sonra, post hoc testlerinden bir tanesini seçiyoruz. Ben burada, en sık kullanılan post hoc testlerinden biri olduğu için Bonferroni’yi seçtim. Veri setinizin özelliğine göre ve hocanızın isteklerine göre başka post hoc testleri de seçebilirsiniz. Farklı post hoc testlerinin ayırt edici özelliklerini daha iyi anlamak için post hoc testleri ile ilgili yazımızı okuyabilirsiniz.
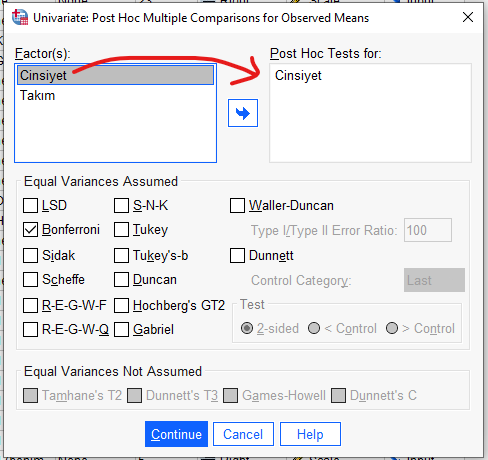
Post hoc testi olarak Bonferroni’yi seçtikten sonra “Continue”ya basıyoruz. Sonra da kalan pencerede “OK”a basıyoruz. SPSS bize analiz sonuçlarını tablolar halinde sunacaktır.
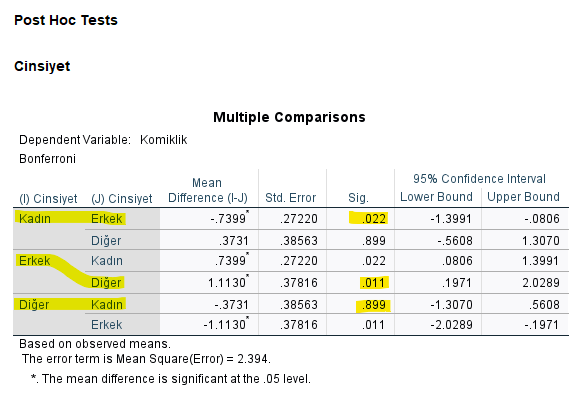
Yukarıdaki post hoc tablosuna göre, kadın ve erkeklerin komiklik skoru arasında anlamlı bir farklılık vardır. Çünkü “Sig.” değeri yani p değeri 0.022 çıkmış. p değeri 0.05’ten küçük olduğu için anlamlı bir fark var diyoruz.
Yukarıdaki post hoc tablosuna göre, erkek ve diğer cinsiyettekilerin komiklik skoru arasında anlamlı bir farklılık vardır. Çünkü “Sig.” değeri yani p değeri 0.011 çıkmış. p değeri 0.05’ten küçük olduğu için anlamlı bir fark var diyoruz.
Yukarıdaki post hoc tablosuna göre, kadın ve diğer cinsiyettekilerin komiklik skoru arasında anlamlı bir farklılık yoktur. Çünkü “Sig.” değeri yani p değeri 0.899 çıkmış. p değeri 0.05’ten büyük olduğu için anlamlı bir fark yok diyoruz.
Basit Temel Etki Analizi (Simple Main Effects = SME Analysis)
İki yönlü ANOVA sonucu, sadece gruplar arasında anlamlı bir fark var mı yok mu onu bize gösterir. Hangi gruplar arasında anlamlı fark olduğuna demin post hoc analizi ile baktık. Fakat, grupları birlikte inceleyerek daha detaylı derinlemesine bir analiz yapmak mümkün.
Örneğin, “erkekler arasında Galatasaraylı ya da Fenerbahçeli olmak acaba komiklik skorunu anlamlı olarak değiştiriyor mu” sorusunun cevabını, post hoc analizi ile bulamadık. Bu şekilde, iki faktörün etkileşiminin gruplar arasında bir fark yaratıp yaratmadığını görmek için ise SME analysis (yani “basit temel etki analizi”) yapmamız gerekiyor.
Eğer iki faktörün etkileşimine bakmayıp sadece bir faktöre göre gruplar arasında fark var mı diye baksaydık, post hoc testi yapmamız yetecekti. Fakat, iki faktörün etkileşimine bakmak, veriyi daha derinlemesine analiz etmemize yarayacak. Bunu da yalnızca SME analysis ile yapabiliyoruz. Bu analizin sonucunda, “Galatasaray’ı tutan kadınların komiklik skoru daha yüksek” gibi, veriyi daha detaylı kategorilere bölerek anlamlı sonuçlar elde etmemiz mümkün olacak.
Şimdi SME analizine başlayalım.
SME analysis yapmak için, SPSS’te yeniden Analyze -> General Linear Model -> Univariate tuşlarına basıp Univariate penceresinde, “EM Means” butonuna basmamız gerekiyor.

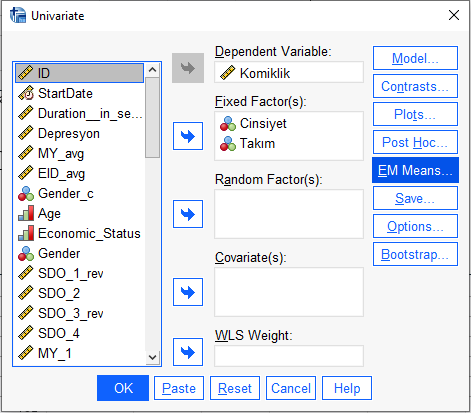
Açılan pencerede, Cinsiyet*Takım etkileşimini, sol kutudan alıp sağ kutuya şekildeki gibi taşımak gerekiyor. Sonra “Continue”ya basacağız.
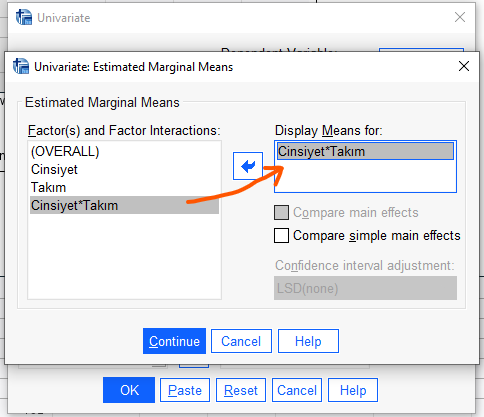
Şimdi, “Univariate” penceresinde, “Paste” butonuna basacağız.
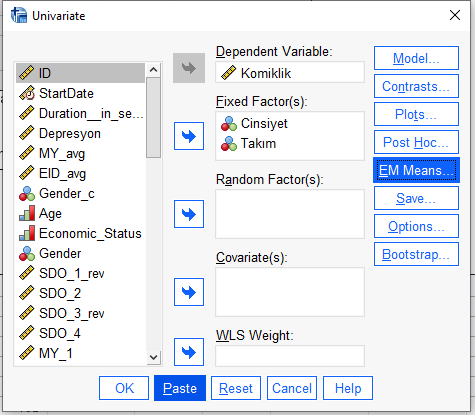
Böyle bir Syntax penceresi açılacak. İçinde kod olması sizi korkutmasın, çok kolay işlemler yapacağız.
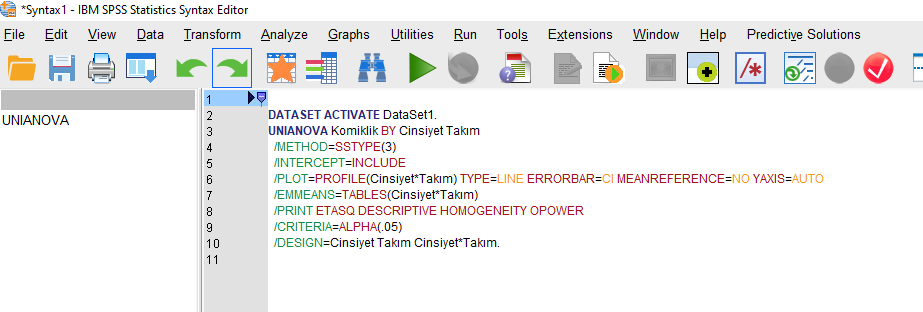
Bu Syntax dosyasında, küçük değişiklikler yapacağız. /EMMEANS ile başlayan 7 numaralı satırdaki yazıyı siliyoruz ve onun yerine şu iki satırı ekliyoruz:
/EMMEANS = TABLES (Cinsiyet * Takım) compare (Cinsiyet) ADJ (BONFERRONI)
/EMMEANS = TABLES (Cinsiyet * Takım) compare (Takım) ADJ (BONFERRONI)
Siz kendi bağımsız değişkenlerinizin adı neyse buraya onları yazarsınız.
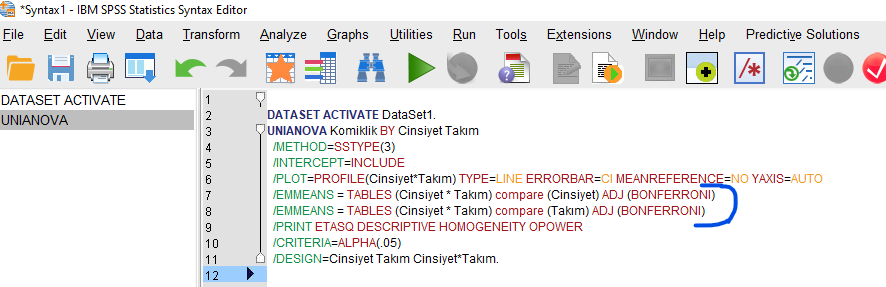
Sonra, bütün kodu fare ile seçip ok ile gösterilen butona basıyoruz.
SPSS analizi yapacak ve bize tabloları verecek.
En önemli tablo, “Pairwise Comparisons” tablosudur. Hatırlarsanız, yukarıdaki “Tests of Between-Subjects Effects” tablosunda, cinsiyetin komiklik skoruna anlamlı etkisi olduğunu, takımın komiklik skoruna anlamlı etkisi olmadığını, cinsiyet ve takımın birlikte değerlendirildiğinde ise komiklik skoruna anlamlı etkisi olduğunu bulmuştuk. Aşağıdaki “Pairwise Comparisons” tablosunda bu etkileri daha detaylı görebileceğiz.
Aşağıdaki tabloda, en üstte işaretli yerde, kadın olup Galatasaray ya da Fenerbahçeli olmanın komiklik skoruna anlamlı bir etkisi olduğunu görebiliyoruz. Çünkü “Sig.” değeri 0.047 çıkmış yani 0.05’ten küçük.
Erkek olup Galatasaray ya da Fenerbahçeli olmanın komiklik skoruna anlamlı bir etkisi olmadığını da görebiliyoruz. Çünkü “Sig.” değeri 0.801 çıkmış yani 0.05’ten büyük.
Diğer cinsiyet olup Galatasaray ya da Fenerbahçeli olmanın komiklik skoruna anlamlı bir etkisi olmadığını da görebiliyoruz. Çünkü “Sig.” değeri 0.731 çıkmış yani 0.05’ten büyük.
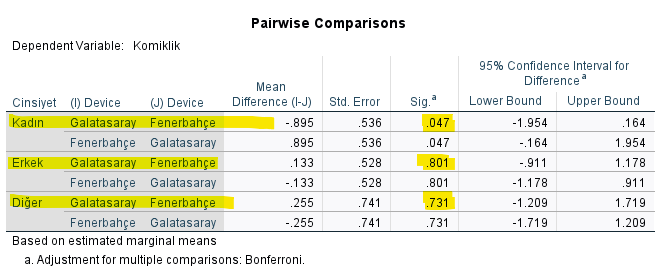
Basit Temel Etki analizi (SME Analysis) yaptığımızda, veri setimizi daha küçük gruplara bölebilmiş oluyoruz ve farkları bu şekilde daha iyi inceleyebiliyoruz. Örneğin, ilk baştaki ANOVA analizinde takımın kendi başına komiklik skoruna etkisi olmadığını bulmuştuk. Fakat, şimdiki ANOVA SME analysis sonucunda, kadın cinsiyetindeki katılımcıların tuttukları takımın komiklik skoruna etkisi olduğunu keşfetmiş olduk. Çünkü verimizi bu analiz sayesinde daha küçük ve detaylı gruplara bölmüş olduk.
Veriyi bir de diğer sırayla bölelim. Demin önce cinsiyete sonra takıma göre bölmüştük. Şimdi de önce takıma sonra cinsiyete göre bölelim ve komiklik skoruna etki var mı diye bakalım.
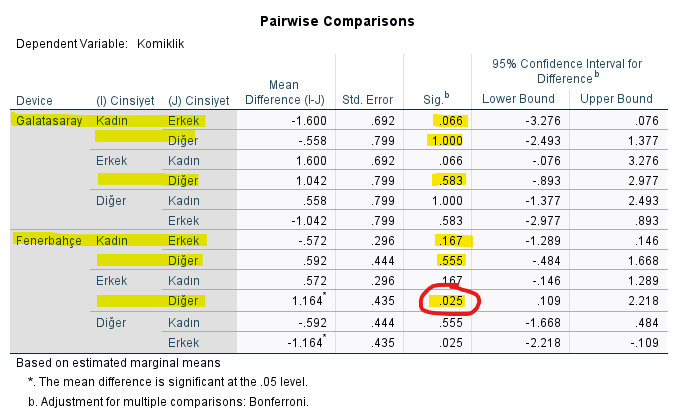
Yukarıdaki tabloda, gördüğünüz gibi, veriyi farklı sırayla gruplara ayırmak bize deminki “Pairwise Comparisons” tablosundan farklı yeni veriler sundu. Bu tabloya göre, yalnızca 1 etkileşimin p değeri 0.05’ten küçük. Kırmızı ile yuvarlak içine aldım. Sadece bu örneği yorumlayacağım, şimdiye kadar yeterince örnek yorumlama yaptım diye.
Yukarıdaki “Pairwise Comparisons” tablosuna göre, “Fenerbahçe’yi tutan katılımcılar arasında, Erkek katılımcılar ve Diğer cinsiyetteki katılımcılar arasında anlamlı bir komiklik skoru farkı vardır” sonucuna varabiliyoruz. Diğer etkileşimlerin p değeri 0.05’ten büyük olduğu için istatistiksel olarak anlamlı değiller.
İki Yönlü ANOVA Etki Büyüklüğü Yorumlama
Kısmi eta-kare (partial eta-squared), iki yönlü ANOVA analizinizi yaptıktan sonra eğer istatistiksel olarak anlamlı bir sonuç bulmanız durumunda, bulduğunuz sonucun ne kadar büyük bir etki büyüklüğüne sahip olduğunu anlamanız için kullanabileceğiniz bir etki büyüklüğü yorumlama ölçüsüdür.
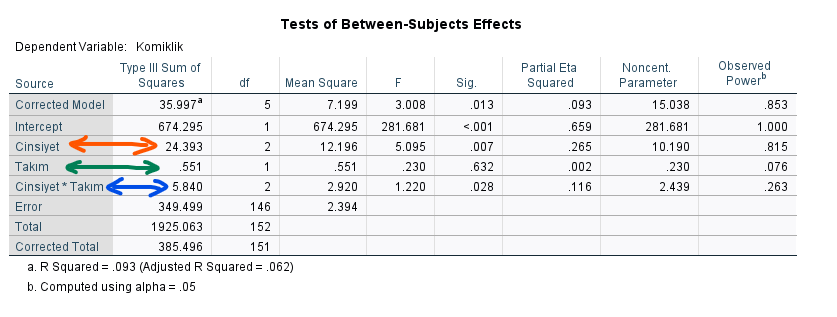
Etki büyüklüğü değerine, ANOVA sonucu bulduğumuz “Tests of Between-Subjects Effects” tablosundan bakabiliriz. Bu tabloda, etki büyüklüğünü ilgili satırın “Partial Eta Squared” değerinden okumamız gerekiyor.
Cinsiyet’in Partial Eta Squared değeri, 0.265’tir. Bu da demek oluyor ki, toplam varyansın %26.5’lik kısmı cinsiyet değişkeni ile açıklanabiliyor.
Takım’ın Partial Eta Squared değeri, 0.002’dir. Bu da demek oluyor ki, toplam varyansın yalnızca %0.2’lik bir kısmı cinsiyet değişkeni ile açıklanabiliyor. Bu mantıklıdır çünkü Takım değişkeni ANOVA sonucunda istatistiksel olarak anlamlı çıkmamıştı.
Son olarak, Cinsiyet ve Takım’ın etkileşiminin Partial Eta Squared değeri, 0.116’dır. Bu da demek oluyor ki, toplam varyansın %11.6’lık kısmı cinsiyet ve takımın birlikte etkileşimi ile açıklanabiliyor.
İki yönlü ANOVA hakkında her şey bu kadardı. İlk olarak ANOVA analizimizi yaptık, daha sonra post hoc testleri yaparak hangi cinsiyetler arasında fark olduğuna ve SME analysis yaparak takım ile cinsiyetin birlikte düşünüldüğünde komiklik skoruna nasıl etki ettiğine baktık. Son olarak da, bulduğumuz istatistiksel olarak anlamlı sonuçların ne kadarlık bir etki büyüklüğüne işaret ettiğini inceledik. Artık, iki yönlü ANOVA analizimizi raporlama aşamasına geçebiliriz.
İki Yönlü ANOVA Sonucu Raporlama (APA)
Aşağıda, örnek bir iki yönlü ANOVA raporu görebilirsiniz. Bu rapordaki değişkenleri ve sayıları kendi deneyinize uydurarak aynı formatta bir ANOVA raporu yazabilirsiniz.
İlk olarak, cinsiyet ve tutulan takım değişkenlerinin komiklik skorları üzerindeki etkilerini değerlendirmek amacıyla iki yönlü ANOVA analizi gerçekleştirildi. Bulgularımıza göre, cinsiyet faktörü açısından istatistiksel olarak anlamlı bir fark tespit edildi (F(2, 146) = 5.095, p = .007). Ancak, takım faktörü arasında anlamlı bir fark saptanmadı (F(1, 146) = 0.230, p = .632). Post hoc testleri uyguladığımızda, erkeklerin, hem kadın hem de diğer cinsiyetlilere göre anlamlı bir biçimde daha yüksek komiklik skoruna sahip olduğunu gözlemledik (p = .022, p = .011).
Daha sonra, cinsiyet ve tutulan takım faktörlerinin birlikte değerlendirildiği SME analizi gerçekleştirildi. Bu analizde, kadınlar arasında Galatasaray ve Fenerbahçeli tutanların komiklik skoru arasında anlamlı bir fark bulundu (p = .047). Aynı zamanda, Fenerbahçeli katılımcılar arasında erkek ve diğer cinsiyettekiler arasında anlamlı bir komiklik skoru farkı bulundu (p = .025).
Son olarak, elde edilen istatistiksel anlamlılıkların etki büyüklüğünü değerlendirdik. Takım faktöründeki eksik anlamlılığa rağmen, cinsiyet faktörü ve cinsiyet ile takım etkileşimi anlamlı etkiler gösterdi. Bu sonuçlar, komiklik skorları üzerindeki değişikliklerde orta ila büyük derecede etki büyüklüklerine işaret etmektedir.






Bir yanıt bırakın