ROC Curve (ROC Eğrisi) Nedir? — Resimli

ROC eğrisi, tıbbi ve veri analizi alanlarında sıklıkla kullanılan önemli bir araçtır. Bu eğri, bir sınıflandırma modelinin performansını değerlendirmek için kullanılır ve modelin hassasiyeti ve özgüllüğü arasındaki dengeyi görselleştirir. ROC eğrisi, farklı kesme noktaları altında duyarlılık ve özgüllük değerlerini gösteren bir grafik olarak tanımlanabilir. Bu değerler, sınıflandırma modelinin performansını belirlemek için kullanılabilir ve aynı zamanda modelin doğruluk oranını ayarlamak için faydalı bilgiler sunar. Bu yazıda, SPSS kullanarak ROC eğrisinin nasıl oluşturulacağı ve yorumlanacağına dair adımları inceleyeceğiz.

ROC Curve (ROC Eğrisi) Nedir?

ROC (Receiver Operating Characteristic) Curve yani ROC Eğrisi, bir sınıflandırma modelinin performansını değerlendirmek için kullanılan grafiksel bir araçtır. Bu eğri, bir sınıflandırıcı modelin duyarlılığı ve özgüllüğü arasındaki ilişkiyi gösterir. Sınıflandırıcı modelin başarısını değerlendirmek için kullanılırken, ROC eğrisi modelin karar eşiği (threshold) değiştiğinde elde edilen duyarlılık (true positive rate) ve özgüllük (true negative rate) oranlarını görsel olarak temsil eder.

ROC eğrisi, iki temel özelliği gösterir:

1. Duyarlılık (Sensitivity veya True Positive Rate – TPR): Duyarlılık, gerçek pozitiflerin (doğru tahmin edilen pozitif sınıf örnekleri) doğru bir şekilde sınıflandırıldığı oranı ifade eder. Matematiksel olarak TPR = TP / (TP + FN), burada TP gerçek pozitif sayısı ve FN yanlış negatif sayısıdır. Duyarlılık, yani TPR, bir modelin gerçek pozitifleri ne kadar başarılı bir şekilde tespit ettiğini gösterir.
2. Özgüllük (Specificity veya True Negative Rate – TNR): Özgüllük, gerçek negatiflerin (doğru tahmin edilen negatif sınıf örnekleri) doğru bir şekilde sınıflandırıldığı oranı ifade eder. Matematiksel olarak TNR = TN / (TN + FP), burada TN gerçek negatif sayısı ve FP yanlış pozitif sayısıdır. Özgüllük, yani TNR, bir modelin gerçek negatifleri ne kadar doğru bir şekilde tespit ettiğini gösterir.

ROC eğrisi, bu iki özelliği (duyarlılık ve özgüllük) farklı karar eşiklerinde (thresholds) değiştirerek çizilir. Karar eşiği, sınıflandırma sonuçlarını pozitif veya negatif olarak belirlemek için kullanılan bir değerdir. Eşik değiştikçe, modelin duyarlılık ve özgüllüğü değişir ve bu değişiklikler ROC eğrisinde görüntülenir.

ROC eğrisi ne zaman kullanılır ve hangi amaçlarla değerlendirilir?

• Model Performansının Değerlendirilmesi: ROC eğrisi, sınıflandırma modelinin genel performansını değerlendirmek için kullanılır. Özellikle dengesiz veri kümelerinde (yani sınıflar arasında önemli oranda farklılık bulunan veri kümelerinde) model performansını değerlendirmek için idealdir.
• Eşik Seçimi: ROC eğrisi, optimum karar eşiğini (threshold) belirlemek için kullanılır. Duyarlılık ve özgüllük arasındaki dengeyi görsel olarak değerlendirerek, modelin ne kadar hassas veya özgül olması gerektiğini belirleyebiliriz.
• Farklı Modellerin Karşılaştırılması: Birden fazla sınıflandırma modelinin performansını karşılaştırmak için ROC eğrileri kullanılabilir. Hangi modelin daha iyi veya daha kötü performans gösterdiği daha net bir şekilde görülebilir.
• Ağ Analizi ve Tıbbi Uygulamalar: ROC eğrisi, tıbbi tanı testlerinin ve diğer ağ analizlerinin performansını değerlendirmek için sıklıkla kullanılır. Testin doğruluğunu ve güvenilirliğini belirlemek için duyarlılık ve özgüllük oranlarına bakılır.

ROC eğrisi, genellikle eğri altındaki alan (AUC – Area Under the Curve) ile birlikte değerlendirilir. AUC, ROC eğrisinin altında kalan alanı ifade eder ve doğruluğun genel bir ölçüsü olarak kullanılır. AUC değeri ne kadar yüksekse, modelin performansı o kadar iyidir. ROC eğrisi ve AUC, sınıflandırma modelinin farklı yönlerini değerlendirmek ve performansını anlamak için güçlü araçlardır.

SPSS ile ROC Analizi Değişkenleri Nasıl Olmalıdır?

ROC eğrisi oluşturarak ROC analizi yapabilmek için 1 adet devamlı veri tipinde bağımsız değişken, 1 adet de yalnızca 2 kategoriye sahip olan bir kategorik değişken gerekmektedir.

SPSS ile ROC Analizi Nasıl Yapılır?

Bu örnekte, bir kişinin SDO isimli bir ölçekteki skoruna bakarak Başarılı olup olmadığını belirlemeye çalışırken duyarlılık ve özgüllük değerlerine ROC Analizi ile bakacağız. SDO ölçeği 1’den 10’a kadar değer alabilen bir ölçek.

Analyze -> Classify -> ROC Curve

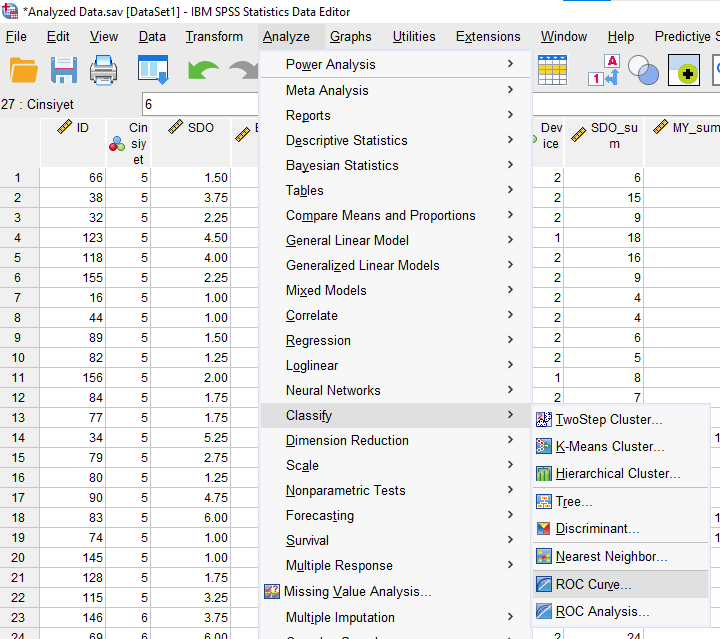
Açılan pencerede bağımlı değişkeni Test Variable, bağımsız değişkeni State Variable kutusuna koyuyoruz. Bağımlı değişken olan Başarı, 5 = Başarısız ve 6 = Başarılı olarak kodlanmıştır. Başarılı olma miktarıyla ilgilendiğimiz için Value Of State Variable kutusuna “6” yazmamız gerekiyor.

Aynı zamanda penceredeki “Display” başlıklı bölümde bütün seçenekleri işaretliyoruz.

“OK”a basıp analizi başlatırsak, SPSS bize karışık çıktılar verecektir. Bunları nasıl yorumlayıp anlamlandırıyoruz teker teker bakalım.

“Case Processing Summary” tablosunda örneğimizdeki kaç kişinin başarılı, kaç kişinin başarısız olduğunu Positive (başarılı) ve Negative (başarısız) satırlarından okuyabiliriz.

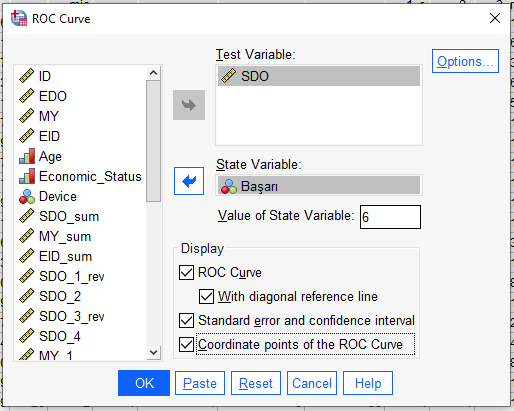
“ROC Curve” başlıklı grafik çok önemli. Bu grafikteki dikey eksen duyarlılık miktarını, yatay eksen de “1 – özgüllük” miktarını göstermektedir.

Bu grafikte diyagonal sol alttan sağ üste giden çizgi referans çizgimizdir. Bu çizginin altında kalan alan toplam grafiğin %50’sidir. Kırmızıyla boyadım aşağıda.

Mavi renkli düzensiz çizgi ise ROC Eğrisi’dir. Bu eğrinin mümkün olduğunca sol üst köşeye yakın geçmesini istiyoruz. Bu eğrinin altında kalan alanın mümkün olduğunca büyük olmasını istiyoruz. Maviyle boyadım aşağıda.

“Area Under the Curve” tablosunda yukarıdaki ROC grafiğiyle ilgili önemli bilgiler var. “Area” bölümündeki değer ROC eğrimizin altında kalan alanı söylüyor. Sig. bölümündeki değer ise ROC eğrisinin altında kalan alanın 0.50’den istatistiksel olarak anlamlı şekilde mi farklı olup olmadığını söylüyor. Lower Bound ve Upper Bound ise, %95 güven aralığında, ROC eğrisinin altında kalan alanın en düşük ve en yüksek ihtimallerini gösteriyor.

Bu örnekte ROC eğrisinin altında kalan alan, grafiğin %50’sinden istatistiksel olarak anlamlı biçimde fazla olacak şekilde grafiğin %64.2’sini kaplıyor. Yani SDO skoru bir kişinin başarılı olup olmaması konusunda anlamlı bir şekilde etki sahibi demektir.

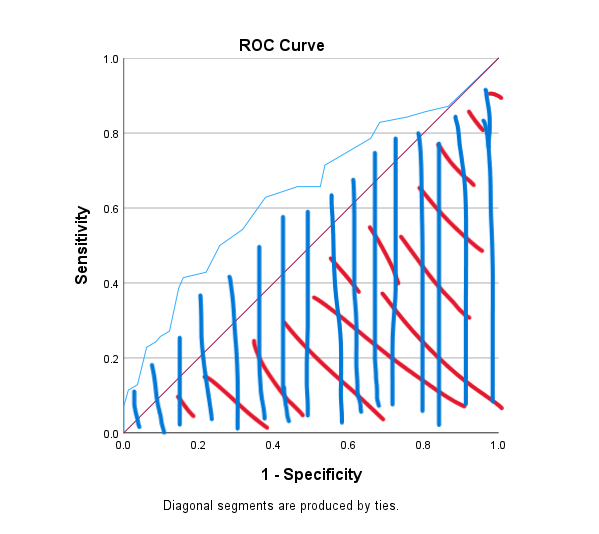
Son olarak “Coordinates of the Curve” tablosunda SDO skorlarının duyarlılık ve özgüllük miktarlarını daha detaylı inceleme şansımız bulunuyor. Burada aynı satırda “Sensitivity” (duyarlılık) ve “1 – Specificity” (1 – özgüllük) miktarlarının ikisinin de mümkün olduğunca büyük olmasını istiyoruz.

Genellikle “Sensitivity”nin 0.80 civarında, “1 – Specificity”nin de 0.20 civarında olmasını istiyoruz. Her ROC eğrisinde bu iki şart aynı anda sağlanmayabiliyor. Bu durumda optimum miktarı belirlemek gerekir.

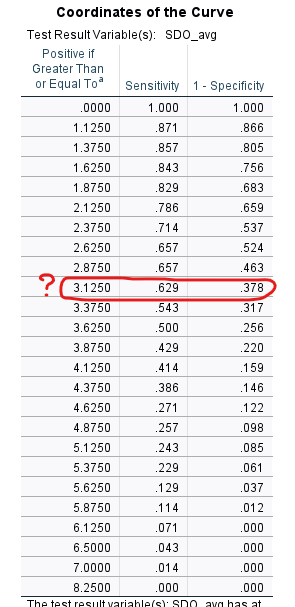
Örneğin bu örnekteki ROC eğrisinde SDO skoru 3.1250 olduğunda Sensitivity 0.629 çıkmış. Bu, modelin gerçek pozitif vakaların yaklaşık %62.9’unu doğru bir şekilde saptayabildiği anlamına gelir. Bu, modelin pozitif vakaları kaçırmama yeteneğini gösterir ve bu oran ne kadar yüksek olursa, model o kadar başarılı olarak kabul edilir.

“1 – specificity” sütunundaki 0.378 değeri, ilgili eşik değeri için özgünlük oranının (specificity) 0.622 (1 – 0.378) olduğunu göstermektedir. Eğer ROC eğrisinin “specificity” değeri 0.622 ise, bu, testin gerçek negatifleri doğru bir şekilde tanımlama miktarının %62.2 olduğunu gösterir.

Yani SDO değeri 3.1250 iken, modelin duyarlılık miktarı 0.629 iken özgüllük miktarı da 0.622 (1 – 0.378) olmaktadır.