
İçindekiler
MANCOVA Analizi, birden çok bağımlı değişkene sahip deney modellerinde grupların arasındaki farklılıkları kovaryantın da etkisini hesaba katarak değerlendirmek için bir ANOVA çeşididir. Bu blog yazısında, MANCOVA Analizi’nin ne olduğunu, analizin varsayımlarını, SPSS ile nasıl gerçekleştirileceğini ve analiz sonuçlarının nasıl yorumlanması gerektiğini ele alacağız.
MANCOVA Analizi Nedir?
MANCOVA Analizi, ANOVA analizinin genişletilmiş versiyonları olan MANOVA ve ANCOVA analizlerinin birleşmesiyle oluşan gelişmiş bir istatistiksel testtir. 1’den fazla bağımlı değişken ve onların etkileşiminin, 1 veya daha fazla bağımsız değişkenin farklı grupları arasındaki ortalama skorlarının farkını, 1 ya da daha fazla kovaryant değişkenin modele etkisini kontrol ederek hesaplamaya yarar.
Aynı “birden fazla ANOVA yapmak yerine 1 adet MANOVA analizi yapmak” mantığı gibi, birden fazla ANCOVA yapmak yerine 1 adet MANCOVA yapmak da daha faydalı bir uygulamadır. Çünkü, 1 adet MANCOVA, gruplar arasındaki ortalama skor farkını tespit etmede birden fazla ayrı ANCOVA analizine göre daha güçlüdür.
MANCOVA’nın temel amacı, kovaryant olarak tanımlanan değişkenlerin, bağımlı değişkenin bağımsız değişkenler tarafından tanımlanan gruplar arasında farklılık görülmesine olan etkisini dikkate alarak, bağımsız değişkenin tek başına bağımlı değişkenler üzerinde anlamlı farklılıklara sebep olup olmadığını belirlemektir. Yani bağımlı değişkenler üzerinde grup ortalamaları arasında fark olup olmadığını test eder ve kovaryantların etkilerini ayarlar. MANCOVA, modelin genel önemi ve bağımsız değişkenlerin belirli etkileri hakkında bilgi sağlayan test istatistikleri üretir.
MANCOVA’nın sonuçlarını yorumlamak, genel modelin anlamlılığını ve bağımsız değişkenlerin bağımlı değişkenler üzerindeki bireysel etkilerini incelemeyi gerektirir. Genel model anlamlı ise, bu bağımsız değişkenlerden en az birinin bağımlı değişkenler üzerinde anlamlı bir etkisi olduğunu gösterir. Araştırmacılar daha sonra hangi belirli grup farklarının anlamlı olduğunu belirlemek için post-hoc testleri veya takip analizlerini kullanabilirler. MANCOVA, psikoloji, eğitim ve sosyal bilimler gibi alanlarda deneysel veya gözlemsel verileri analiz etmek için yaygın olarak kullanılmaktadır ve potansiyel karıştırıcı değişkenleri kontrol eder.
MANCOVA Örneklemi Nasıl Olmalı?
Tipik bir MANCOVA analizi örneklemi aşağıdaki gibidir:
Bağımsız Değişken: 1 ya da daha fazla bağımsız değişken olabilir. Bağımsız değişkenler kategorik olmalıdır. Eğer 1 bağımsız değişken varsa buna Tek Yönlü MANCOVA denir, 1’den fazla ise İki veya Çok Yönlü MANCOVA denir.
Bağımlı Değişken: En az 2 tane bağımlı değişken olmalıdır. Bu değişkenler sürekli veri tipinde olmalıdır.
Kovaryant: En az 1 tane kovaryant olmalıdır. Kovaryant da sürekli veri tipinde olmalıdır.
MANCOVA Analizi Varsayımları
MANCOVA analizi yapmadan önce, bazı varsayımların sağlanması gerekmektedir. Bunlar ANOVA, MANOVA ve ANCOVA varsayımlarının birleşimi gibi düşünülebilir. MANCOVA varsayımları aşağıdaki gibidir:
- Normal Dağılım Varsayımı: Normalde MANOVA ve MANCOVA’da çoklu normallik (multivariate normality) varsayımı test edilmelidir. Fakat bu SPSS’te test edilemiyor. Bu yüzden, sosyal bilimlerde sıkça kullanılan alternatif yöntem, bütün bağımlı değişkenlerin tek başına ele alındığında normal dağılıp dağılmadığını kontrol etmektir. Normal dağılıma sahip olmayan verilerde MANCOVA sonuçları güvenilir olmayabilir.
- Uç Değer Olmaması Varsayımı: ANOVA varyasyonları parametrik testler oldukları için, veride uç değer olmasına karşı hassastırlar. Tekli ve çoklu uç değerlerin önceden tespit edilip MANCOVA analizine başlanmadan önce veriden çıkartılması gerekmektedir.
- Lineer İlişki Varsayımı: Bütün bağımlı değişkenlerin birbirleriyle ve kovaryant değişken ile bir miktar korelasyon göstermesi gerekmektedir. Bu korelasyonun miktarı çok düşük (mesela 0.1’den küçük) veya çok büyük (mesela 0.8’den büyük) olmasa iyi olur.
- Varyans-Kovaryans Matrislerinin Homojenliği Varsayımı: Bu varsayım, farklı gruplar arasındaki bağımsız değişkenlerin etkisinin bağımlı değişkenler üzerinde aynı varyans yapısına sahip olduğunu ifade eder. Yani, MANCOVA analizi yaparken, her bir grup için bağımlı değişkenlerin varyanslarının ve kovaryanslarının benzer olması gerektiğini varsayar. Box’s M Test ile test edilir.
- Regresyon Eğrilerinin Homojenliği Varsayımı: Kovaryant ile bağımsız değişken(ler), istatistiksel olarak anlamlı bir şekilde interaksiyon göstermemelidir.
Varsayımlar doğrulanmazsa, MANCOVA analizi sonuçları güvenilir olmaz, o zaman MANCOVA yerine farklı analiz yöntemleri kullanmak veya istatistiksel sonuçların yorumlanmasında dikkatli olmak gerekebilir.
Bağımlı değişkenler hiç korelasyon göstermiyorsa ya da çok fazla (0.8-0.9) korelasyon gösteriyorsa 1 adet MANCOVA analizi yerine ayrı ayrı ANCOVA analizleri yapmak daha doğru olacaktır.
SPSS ile MANCOVA Analizi Varsayımları Test Etme
SPSS ile MANCOVA analizinin varsayımlarını aşağıdaki gibi test ediyoruz.
Bu sayfada yapacağımız MANCOVA örneğinde, farklı Cinsiyetler arası (erkek, kadın, diğer) okul Performansında ve/veya Motivasyonunda farklılık var mı diye bakacağız ve bunu Sosyal Destek faktörünün göz önüne alındığı durumda yapacağız.
Normal Dağılım ve Tekli Uç Değer Varsayımı
Analyze -> Descriptive Statistics -> Explore
Bütün bağımlı değişkenlerle kovaryantı Dependent List kutusuna atıyoruz.
“Statistics” butonuna basarak açılan yeni pencerede “Outliers”ı işaretliyoruz.
“Plots” butonuna basarak açılacak yeni pencerede Boxplots, Histogram ve Normality Plots seçeneklerini işaretliyoruz.
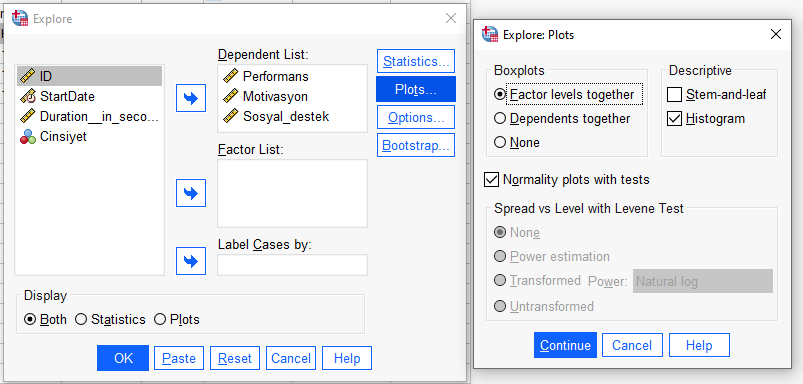
Continue ve OK’a basarsak SPSS’in bize vereceği tablolara bakabiliriz artık. Normal dağılımı test etmek için Tests of Normality tablosundaki Sig. sütunundaki değerlere bakmalıyız. Bu değerler 0.05’ten büyükse normal dağılım varsayımı sağlanmış diyebiliriz. Normal dağılım olup olmadığına karar vermek hakkındaki detaylı yazımı linkten okuyabilirsiniz.
SPSS aynı zamanda her değişken için bir adet kutu grafiği sunacak. Aşağıya bir tanesini örnek olarak koydum. Bu grafiklere bakarak tekli uç değerleri bulabiliyoruz. Bu kutu grafiklerinin kırmızı ile işaretlediğim alanı dışında, aşağıda veya yukarıda herhangi bir nokta bulunmaması idealdir. Uç değer tespiti ve tespiti durumunda ne yapılması gerektiği hakkındaki detaylı yazımı linkten okuyabilirsiniz.
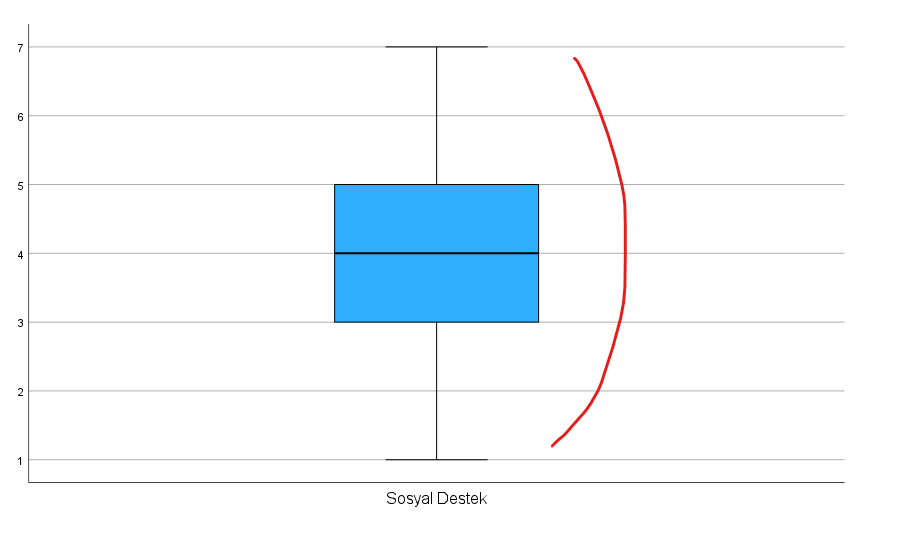
Lineer İlişki Varsayımı
Graphs -> Scatter/Dot
Matrix Scatter seçip Define’a basıyoruz.
Açılan pencerede kovaryant ve bağımlı değişkenlerimizin hepsini Matrix Variabes bölümüne atıp OK’a basıyoruz.
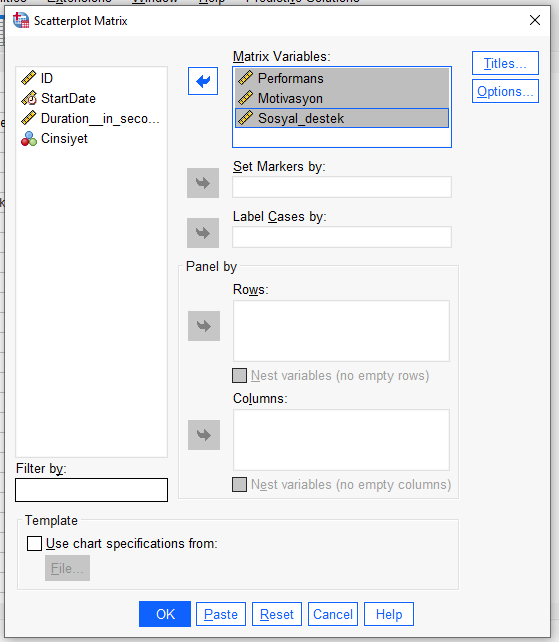
SPSS’in bize vereceği grafikte, her hücre içindeki noktaların dağılımını incelememiz gerekiyor şimdi. Kırmızı ile çizdiğim şekilde, sol alttan başlayarak sağ üste giden (ya da sol üssten sağ alta) bir şekilde noktalar dağılım gösteriyorsa bu idealdir.
Aşağıdaki örnekte noktaların dağılımı ideal değil, biraz daha iyi incelenmesi gerekiyor. Aşırı kötü de değil, ufak da olsa bir yönelim var. Bu örnekte noktalar bizim istediğimiz şekilde bir dağılım gösteriyor diye kabul edip MANCOVA analizimize devam edebiliriz.
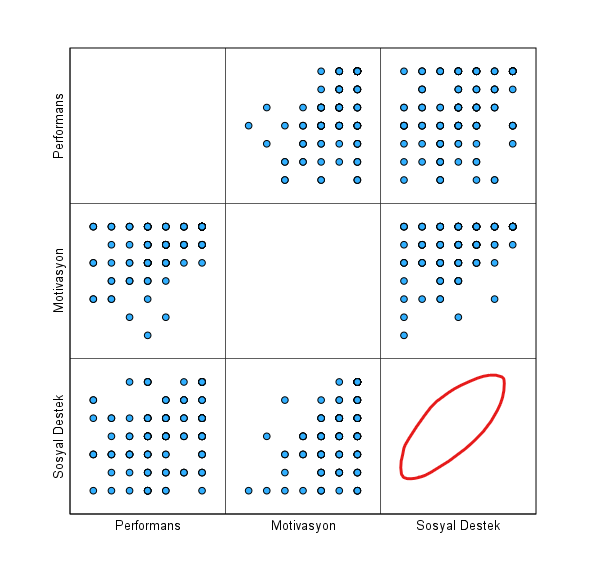
Varyans-Kovaryans Matrislerinin Homojenliği & Regresyon Eğrilerinin Homojenliği
Bu iki varsayımı test etmek için, önden bir MANCOVA analizi yaparmış gibi yapıyoruz. Bu, en son yapacağımız MANCOVA değil. Sadece varsayımları test etmek için uyguladığımız bir ön analiz.
Analyze -> General Linear Model -> Multivariate
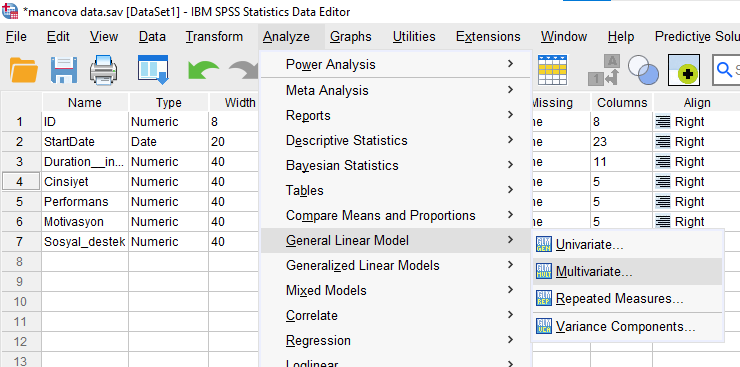
Açılan pencerede bütün değişkenlerimizi ait oldukları kutuya koyuyoruz. Sosyal Destek kovaryant olduğu için Covariates, Cinsiyet bağımsız değişken olduğu için Fixed Factors, Performans ve Motivasyon da bağımlı değişkenler olduğu için Dependent Variables kutularına yerleştirildi.
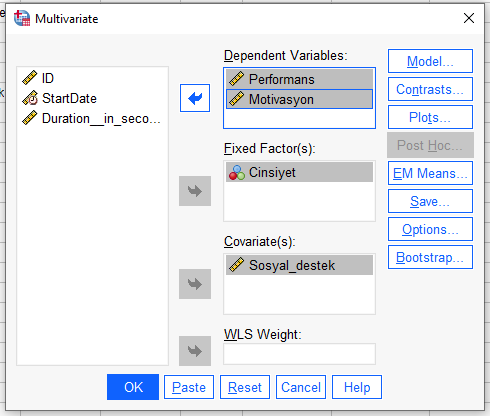
Aynı penceredeki “Model” butonuna basıyoruz. Açılacak yeni pencerede, “Custom” Model seçeneğini işaretliyoruz. Daha sonra, soldaki kutudan sağdaki Model kutusuna önce sadece Cinsiyet’i, sonra sadece Sosyal Destek’i, sonra da ikisini birlikte seçip ikisini birlikte taşıyoruz. Sonra “Continue”ya basıyoruz.
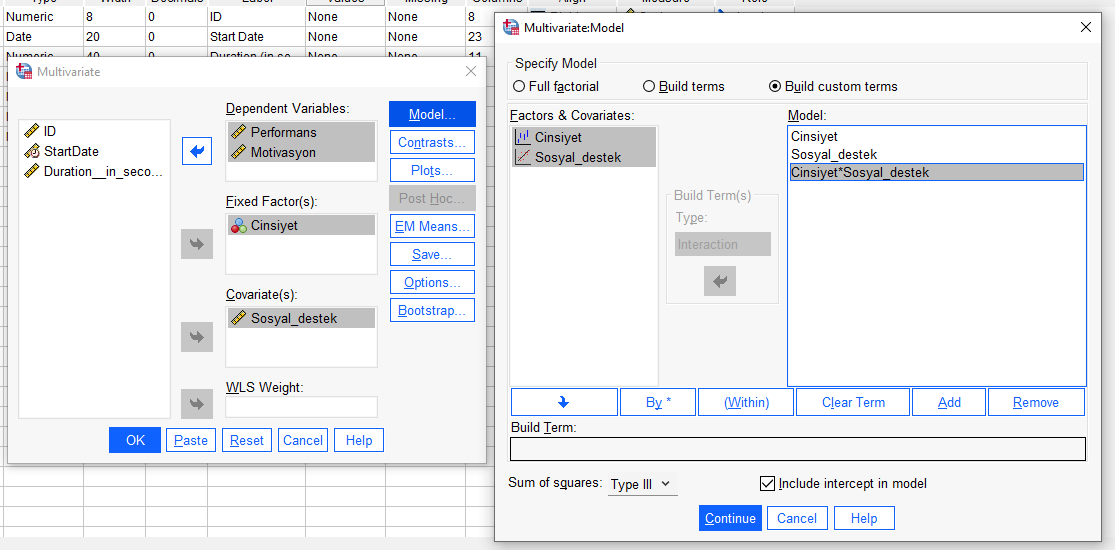
“Options”a basarak açılacak yeni pencerede Homogeneity Tests seçeneğini işaretliyoruz.
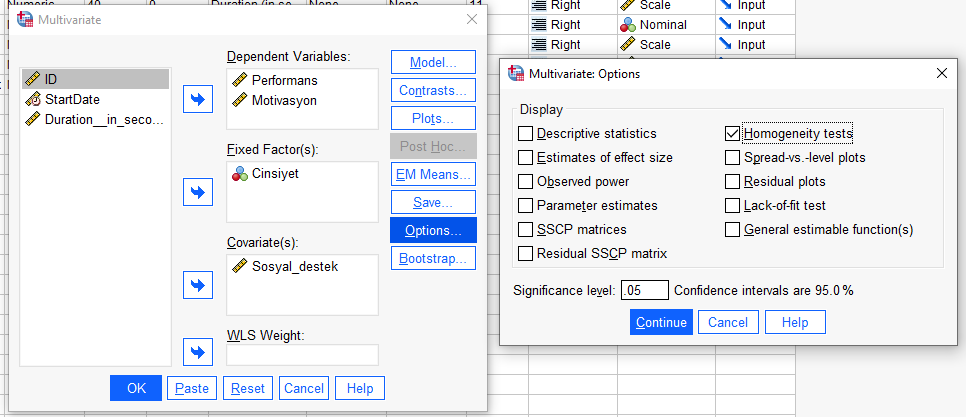
Continue ve OK’a basarsak SPSS bize varsayımları kontrol edeceğimiz tabloları verecek.
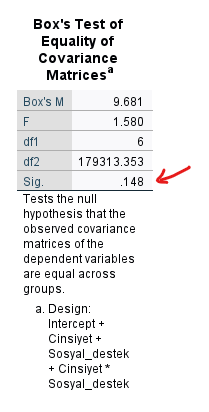
Öncelikle, varyans-kovaryans matrisinin homojenliğini kontrol etmek için Box’s Test tablosunun Sig. p değerine bakıyoruz. Bu testin p değerinin büyük olmasını istiyoruz. Box’s M testine özel olarak eşik p değeri her zamanki 0.05 değil, 0.01 veya 0.005 veya 0.001 olarak daha sık kullanılmaktadır. Bizim örneğimizde Box’s M Sig. p değeri hepsinden büyük olduğu için sorun yok, varyans-kovaryans matrislerinin homojenliği varsayımı sağlandı diyebiliriz.
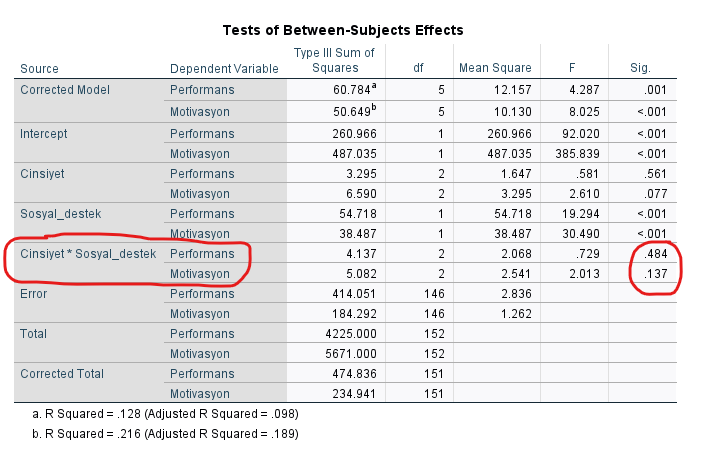
Regresyon eğrilerinin homojenliği varsayımını da “Tests of Between Subjects Effects” tablosuna bakarak test ediyoruz. Bu tabloda sadece iki değişkenin birleşiminin olduğu bölümde her bağımlı değişken satırı için Sig. p değerine bakmalıyız. Yine, varsayımı doğrulayabilmek için p değerinin büyük olmasını istiyoruz. Bu örneğimizde p değerleri 0.484 ve 0.137 yani ikisi de 0.05’ten büyük olduğu için bu varsayımı da doğruladığımızı söyleyebiliriz.
Çoklu Uç Değer Olmaması Varsayımı
Son olarak, MANCOVA da MANOVA’nın bir genişletilmiş versiyonu olduğu için, MANOVA analizinde yaptığımız gibi, Mahalanobis uzaklığı ile çok değişkenli uç değere sahip olan katılımcıları tespit edip MANCOVA öncesinde veri setimizden çıkartmalıyız. Mahalanobis uzaklığı SPSS’te şöyle bulunuyor:
Analyze -> Regression -> Linear
Yapacak olduğumuz MANCOVA’da baağımlı değişkenlerimizin hepsini birlikte Independents kutusuna atıyoruz. Dependent kutusuna herhangi bir değişkeni atmalıyız yoksa SPSS analizi çalıştırmayacak (buraya ne attığımız fark etmez). “Save” butonuna basıp açılan yeni pencerede “Mahalanobis” işaretliyoruz. Continue ve OK.
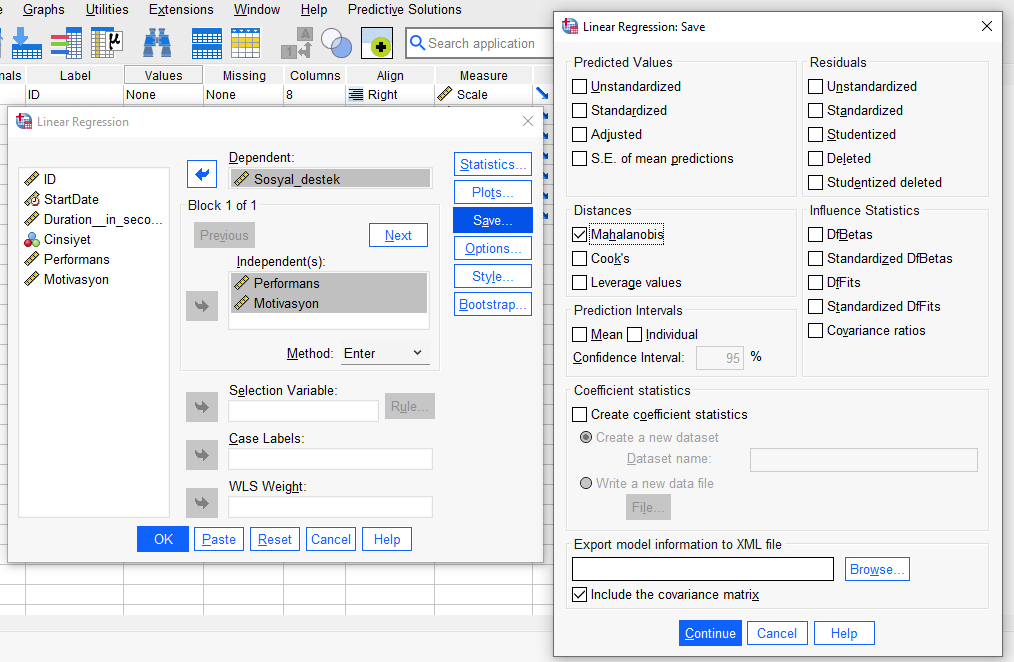
SPSS veri setimizin en sağ sütununa bakarsak burada yeni bir MAH_1 isminde sütun açılmış olduğunu göreceğiz. Bu sütun her katılımcının bağımlı değişkenlerinin skorları kombine edilerek hesaplanan Mahalanobis uzaklıklarını içermektedir. Olması gereken eşik değerinden büyük Mahalanobis uzaklığına sahip katılımcılar varsa bunları bu sütunda tespit edip MANCOVA analizimiz öncesinde veriden çıkartmamız gereklidir.
Eşik değeri olarak hangi sayıyı kullanacağımız verinin tipine göre değişmektedir. Bu sayfayı gereksiz uzatmaması adına Mahalanobis uzaklığı eşik değeri ve yorumlama hakkında detaylı yazımın linkini buraya koyuyorum, tıklayıp okuyabilirsiniz.
Bu örnekteki gibi 2 değişkenli örneklemlerde eşik değeri 11 olduğu için 11’den büyük Mahalanobis uzaklığına sahip katılımcıları veriden çıkartıyorum. Artık gerçek MANCOVA analizimize başlayabiliriz.
SPSS ile MANCOVA Analizi Nasıl Yapılır?
SPSS ile MANCOVA analizi yapmak için aşağıdaki adımları takip etmek gerekiyor:
Analyze -> General Linear Model -> Multivariate

Açılan pencerede bütün değişkenlerimizi ait oldukları kutuya koyuyoruz. Sosyal Destek kovaryant olduğu için Covariates, Cinsiyet bağımsız değişken olduğu için Fixed Factors, Performans ve Motivasyon da bağımlı değişkenler olduğu için Dependent Variables kutularına yerleştirildi.

“Model” butonuna tıklayıp Model’i yeniden Full Factorial’a getirmek gerekiyor. Sonra Continue.
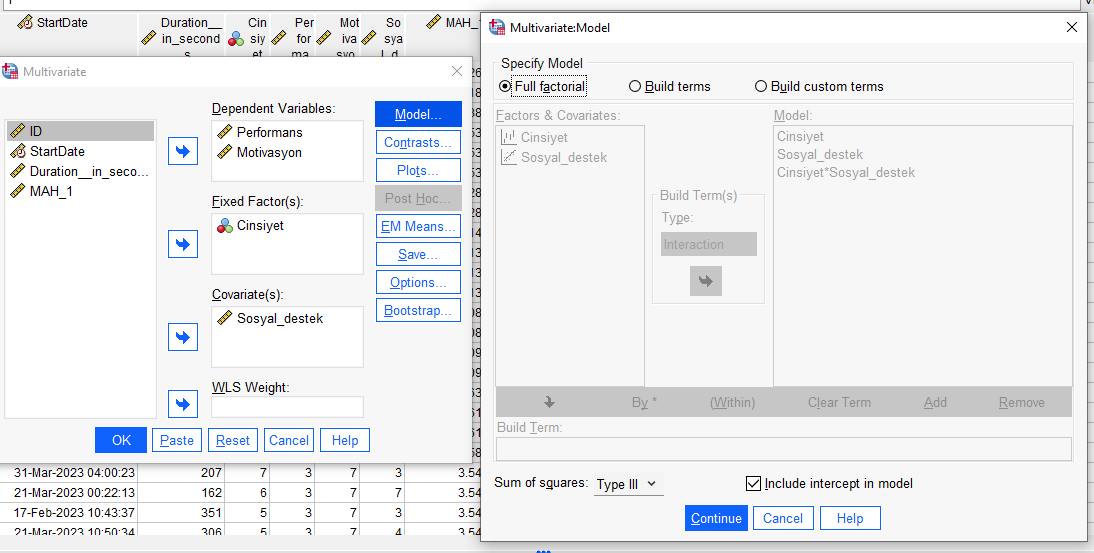
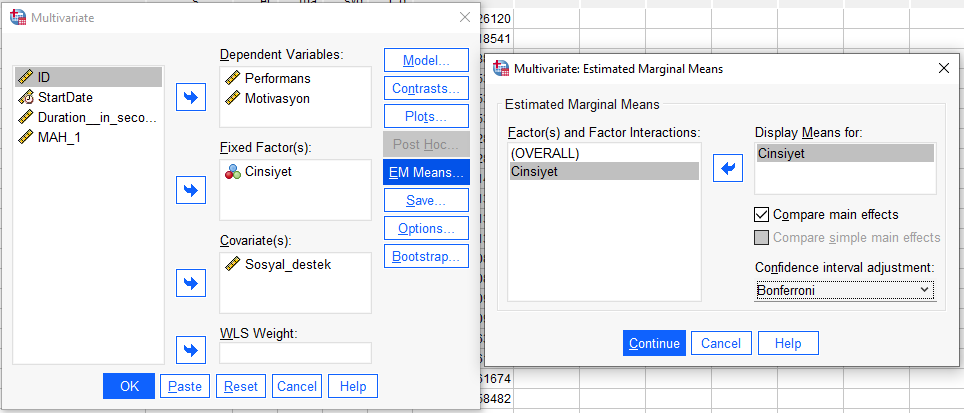
“EM Means”e basıp Cinsiyet’i sağdaki kutuya atıp Compare Main Effects işaretleyip Confidence Interval Adjustment’ı Bonferroni’ye getirmek gerekiyor. Bu hangi Cinsiyet grupları arasındaki farkların istatistiksel olarak anlamlı olduğunu Tip I Hata miktarını düşük tutarak keşfetmeye yarayacak.
“Options”a basıp Descriptive Statistics, Effect Size ve Homogeneity Tests’i işaretliyoruz.
“Plots”a basarak Cinsiyet’i Horizontal Axis’e koyup “Add” butonuna basıyoruz. Sonra Continue.
Her şeyi bitirdikten sonra Multivariate penceresinde “OK” butonuna basarak MANCOVA analizimizi başlatabiliriz.
MANCOVA Analizi SPSS Tablo Yorumlama
SPSS, bize bir sürü MANCOVA analizi sonuç tablosu verecektir. Bunların arasından hangi tabloların nerelerine bakmak gerektiğini aşağıda anlatıyorum.
İlk başta Box’s M Test tablosuna bakmamız gerekiyor. Buna demin bakmıştık, yine aynı değer çıkacaktır. Eşik p değerinden büyük olduğu için MANCOVA sonuçlarımızın güvenilir olacağı sonucuna varabiliriz buradan.
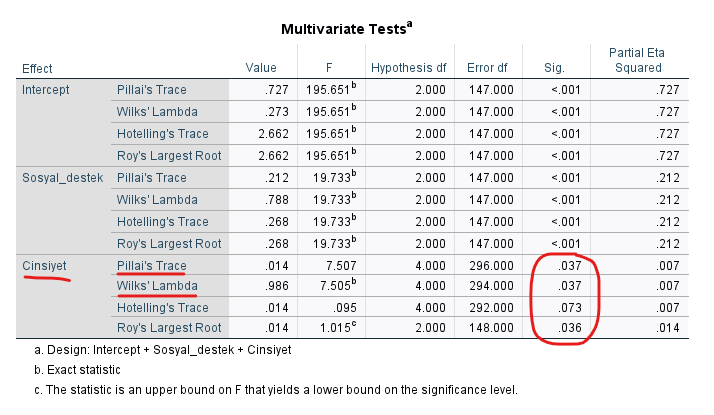
Öncelikle “Multivariate Tests” tablosuna bakmalıyız. Burada Cinsiyet bölümündeki 4 MANCOVA test istatistiği çeşidinden birini seçmeliyiz. MANOVA başlıklı yazımda da bahsettiğim üzere, eğer MANOVA analizinden önce yaptığımız varsayım testlerinin hepsi varsayımları doğruluyorsa, Wilks’ Lambda seçmek daha doğru olacaktır. Eğer MANOVA analizinden önce yaptığımız varsayım testleri sonucunda bazı varsayımları doğrulayamadıysak o zaman Pillai’s Trace seçmek daha doğru olacaktır çünkü Pillai’s Trace testi diğerlerine göre varsayım ihlallerine daha dayanıklıdır.
Bu sayfadaki örnekte yukarıda hatırlarsanız kovaryant ve bağımlı değişkenler birbirleriyle çok doğrusal bir korelasyon ilişkisi göstermemişti (Scatterplot grafikleri). Varsayımları ideal şekilde doğrulayamadığımızı düşünerek, bu MANCOVA analizi için test istatistiği olarak Pillai’s Trace seçmemiz daha uygun olacaktır.
Pillai’s Trace Sig. p değeri 0.037 çıkmış. Bu 0.05 p eşik değerinden küçük olduğu için, diyoruz ki: “MANCOVA analizi sonucu, Sosyal Destek kontrol edildiğinde bile en az 2 Cinsiyet grubu arasında Performans ve/veya Motivasyon yönünden farklılık bulunmaktadır”.
Cinsiyetler arasında Performans yönünden mi yoksa Motivasyon yönünden mi farklılık bulunduğunu aşağıda “Tests of Between-Subjects Effects” tablosundan öğreneceğiz fakat oraya bakmadan önce “Levene’s Test of Equality of Error Variances” tablosuna bakmalıyız.
Bu tabloda bütün bağımsız değişkenlerin Sig. p değerinin 0.05’ten büyük olmasını istiyoruz. O zaman alttaki ANOVA tablosunun sonuçları daha güvenilir olacaktır.
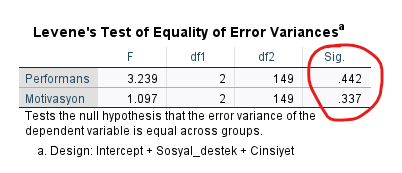
“Tests of Between-Subjects Effects” tablosunu, her bağımlı değişken için ayrı ayrı yapılan ANOVA’ların sonuçları gibi düşünebilirsiniz. Burada Performans’ın Sig. p değeri 0.029, Motivasyon’unki 0.425 çıkmış. Deminki yorumlamamızı şu şekilde güncelleyebiliriz demek ki: “MANCOVA analizi sonucu, Sosyal Destek kontrol edildiğinde bile en az 2 Cinsiyet grubu arasında Performans yönünden farklılık bulunmaktadır”.
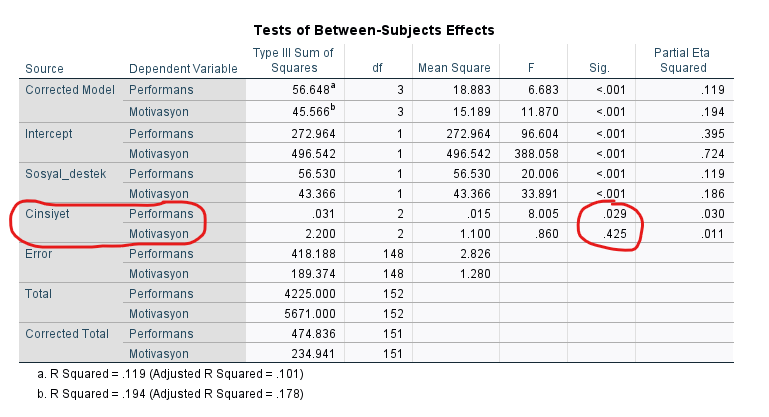
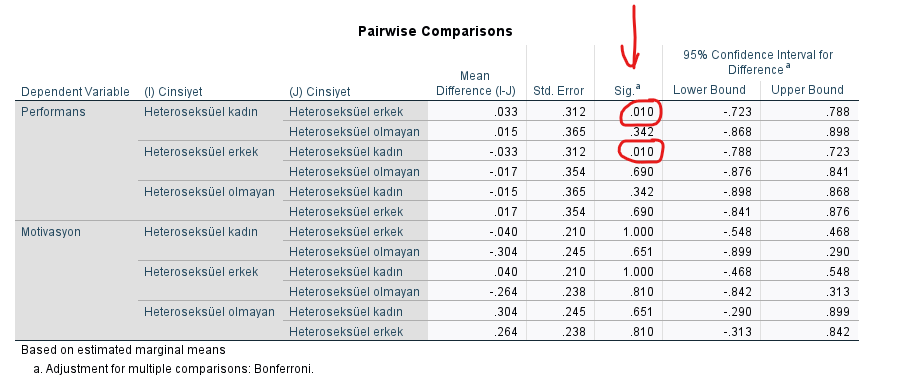
Performans yönünden hangi Cinsiyet grupları arasında anlamlı farklılık bulunduğunu da “Pairwise Comparisons” tablosundan öğreniyoruz. Aşağıdaki tabloda, Kadın ve Erkek değişkenlerinin birlikte olduğu satırda Sig. p değeri 0.010 çıkmış. Bu değer 0.05’in altında çıkan başka bir Cinsiyet çifti yok.
O zaman en son yorumlamamızı şöyle güncelleyebiliriz: “MANCOVA analizi sonucu, Sosyal Destek kontrol edildiğinde bile Kadın ve Erkek katılımcılar arasında Performans yönünden farklılık bulunmaktadır”.
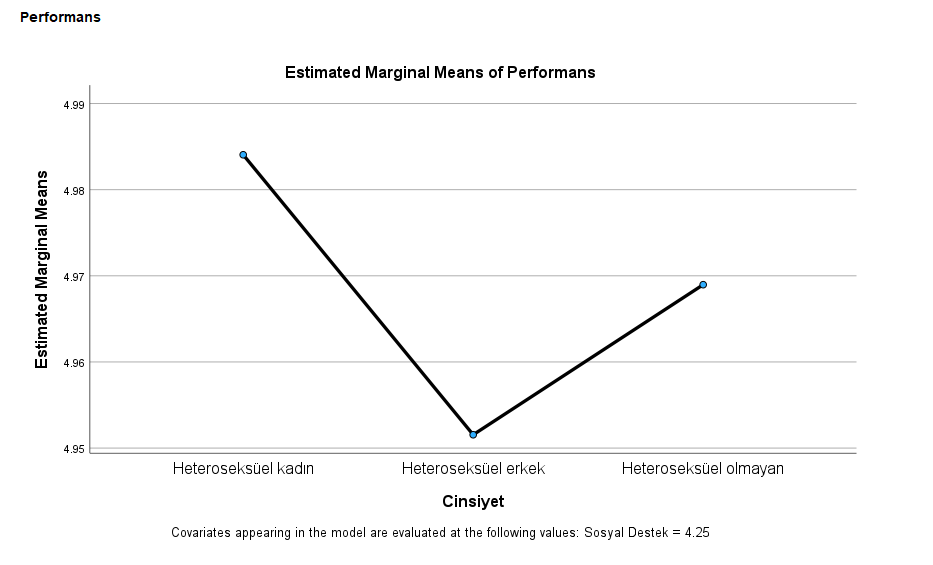
MANCOVA analizi sonuçlarımızı grafikler ile de görelim.
Performans’a ait olan grafikte görüyoruz ki Kadın en yüksek Performans, Diğer cinsiyet orta sırada Performans, Erkek cinsiyet de en düşük Performans’ı göstermiş. Bu Performans farklarından sadece Kadın ve Erkek’in arasındaki Performans farkı istatistiksel olarak anlamlıymış.
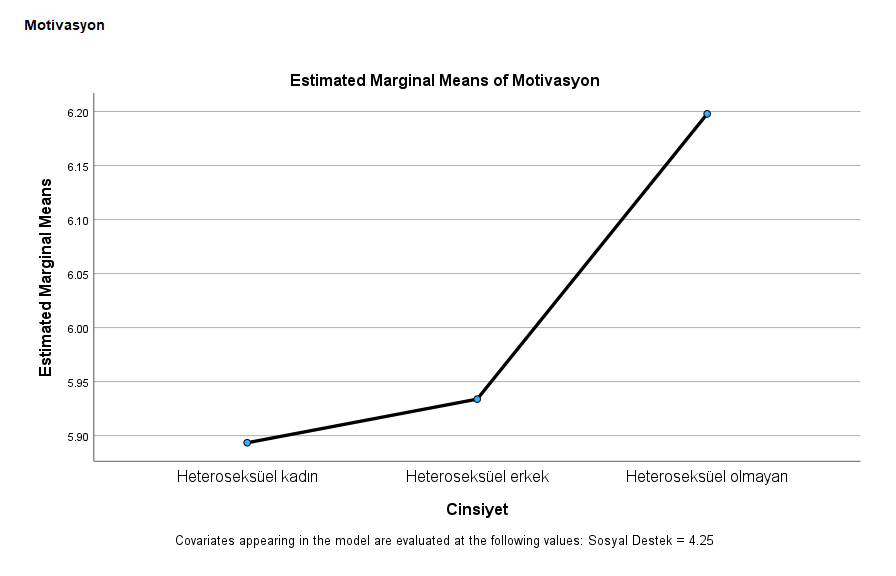
Motivasyon’a ait olan grafikte görüyoruz ki Diğer cinsiyetteki katılımcılar en yüksek Motivasyon, Erkek katılımcılar orta sırada Motivasyon, Kadın katılımcılar da en düşük Motivasyon’u göstermiş. Fakat bu Motivasyon farklarından hiçbiri istatistiksel olarak anlamlı çıkmadığı için, Cinsiyetler arası herhangi bir anlamlı Motivasyon seviyesi farkından söz edemeyiz.
Sonuç & Daha Fazla Değişkenli MANCOVA
MANCOVA analizi varsayımları ile beraber SPSS’te yapılıp tablolarının yorumlanışı bu kadardı. Buraya kadar okuduysanız artık kendi MANCOVA analizinizi gerçekleştirme becerisini kazanmış oldunuz. Bu örnekte basit olması adına sadece 2 bağımlı değişken, 1 bağımsız değişken ve 1 kovaryant kullanarak MANCOVA analizi yapmayı gösterdim.
Daha fazla bağımlı değişken ile 1’den fazla bağımsız değişken ve/veya kovaryant kullanarak MANCOVA analizini genişletmek de mümkün. Tabloları okumak daha uzun sürecektir fakat İki Yönlü MANOVA ve İki Yönlü ANCOVA hakkındaki yazılarımı okuyup oradaki uygulamaları bu sayfadaki MANCOVA analizi örneğiyle birleştirirseniz istediğiniz her türden her sayıda değişkene sahip MANCOVA analizleri yapabilmiş olacaksınız.






Bir yanıt bırakın